中国海洋大学2023计算机系统基础复习大纲(1-2章)

第一章 计算机系统概述

程序和指令的执行过程

1. 根据PC取指令（取菜谱）
2. 指令译码（读菜谱）
3. 取操作数（取原材料）
4. 指令执行（做菜）
5. 回填结果（装盘）
6. PC+1（做下一道菜）

程序设计语言和翻译程序

机器语言：0/1序列

机器级语言：汇编语言和机器语言

高级程序设计语言（高级编程语言）：BASIC、C/C++、Fortran等

从源程序到可执行程序

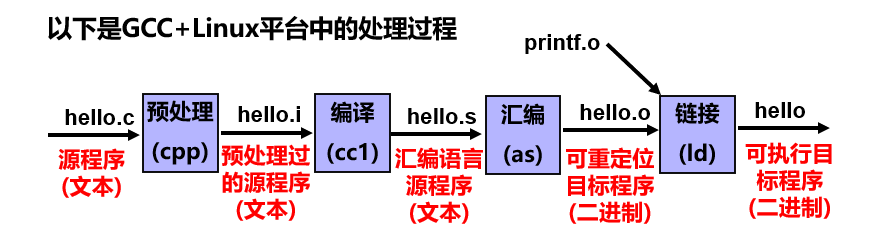
1. 预处理：如将头文件嵌入到源程序文件（.h到.i）
2. 编译阶段：
3. 汇编阶段
4. 链接：形成可执行文件

计算机抽象层的转换

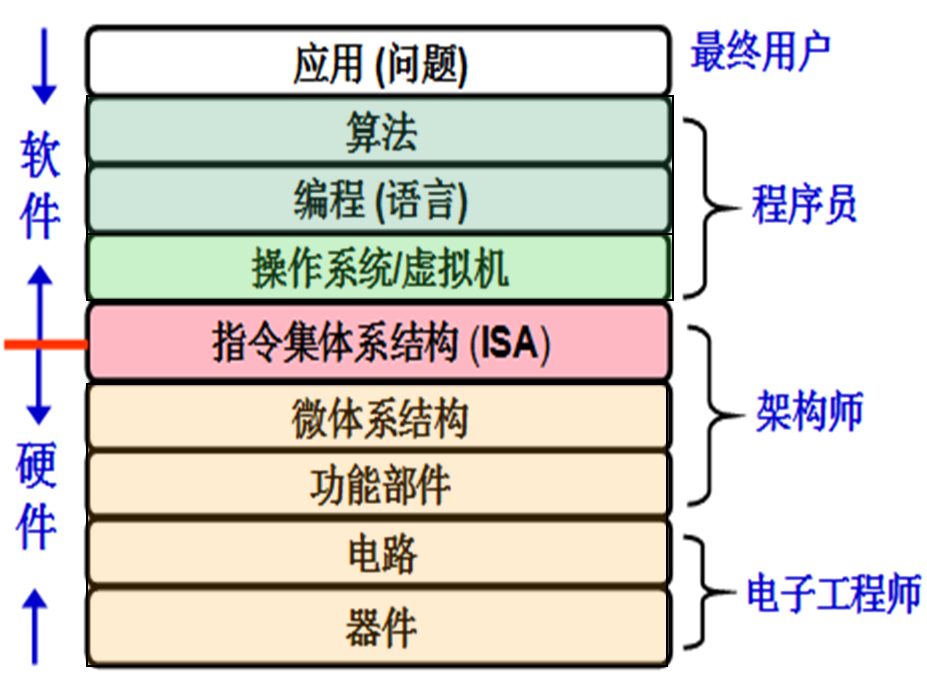
指令集体系结构ISA：简称体系结构或系统结构，定义了一台计算机可以执行的所有指令的集合。

计算机系统性能评价

• G是10的九次方，M是10的六次方

CPU时间

用户CPU时间：指真正用于运行用户程序代码的时间

系统CPU时间：指为了执行用户程序而需要CPU运行操作系统程序的时间

其他时间

• 系统性能和CPU性能并不等价。系统性能是指系统的响应时间，它与CPU外的其他部分也有关系。而CPU性能是指用户CPU时间

时钟周期

CPU的主脉冲信号宽度称为时钟周期

时钟频率

CPU的主脉冲信号的始终频率，时钟周期的倒数

CPI

表示执行一条指令所需时钟周期数。由于不同指令的功能不同，所需的时钟周期数也不同。执行一条指令所需要的时钟周期数或者平均时钟周期数

MIPS

平均每秒执行指令的条数（以百万条为单位）

计算公式

CPU执行时间 = CPU时钟周期数 * 时钟周期

​ = CPU时钟周期数 / 时钟频率

​ = 指令条数 * CPI * 时钟周期

​ = 指令条数 / MIPS * 10e6

CPU时钟周期数 = 指令条数 * CPI

​ = CPU执行时间 / 时钟周期

​ = CPU执行时间 * 时钟频率

​ 假定CPIi 和 Ci分别是第 i 类指令的CPI 和指令条数，则程序的总时钟数为

\[CPU时钟周期数 = \sum_{i=1}^{n} CPI_i * C_i \]

CPI = CPU时钟周期数 / 指令条数

​ 假定CPIi、 Fi是第i类指令的CPI和在程序中的出现频率，则程序综合CPI为

\[CPI = \sum_{i=1}^{n}CPI_i * F_i \\ where F_i = \frac{C_i}{Instruction\_Count} \]

MIPS

\[MIPS = \frac{指令条数}{执行时间 * 10^6}\\ =\frac{指令条数}{CPU时钟周期总数*10^6/主频}\\ = \frac{f}{CPI*10^6} \]

例题

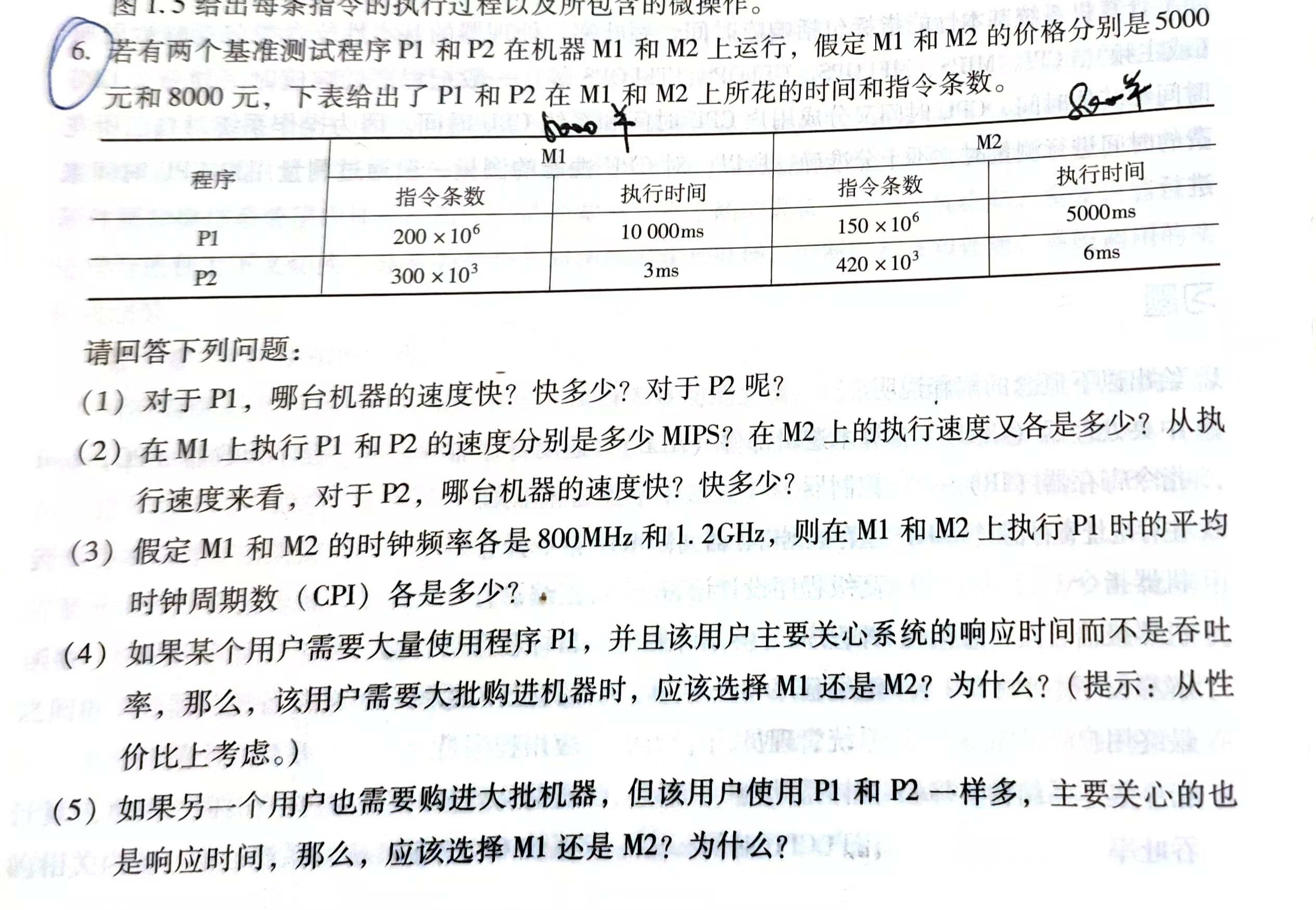
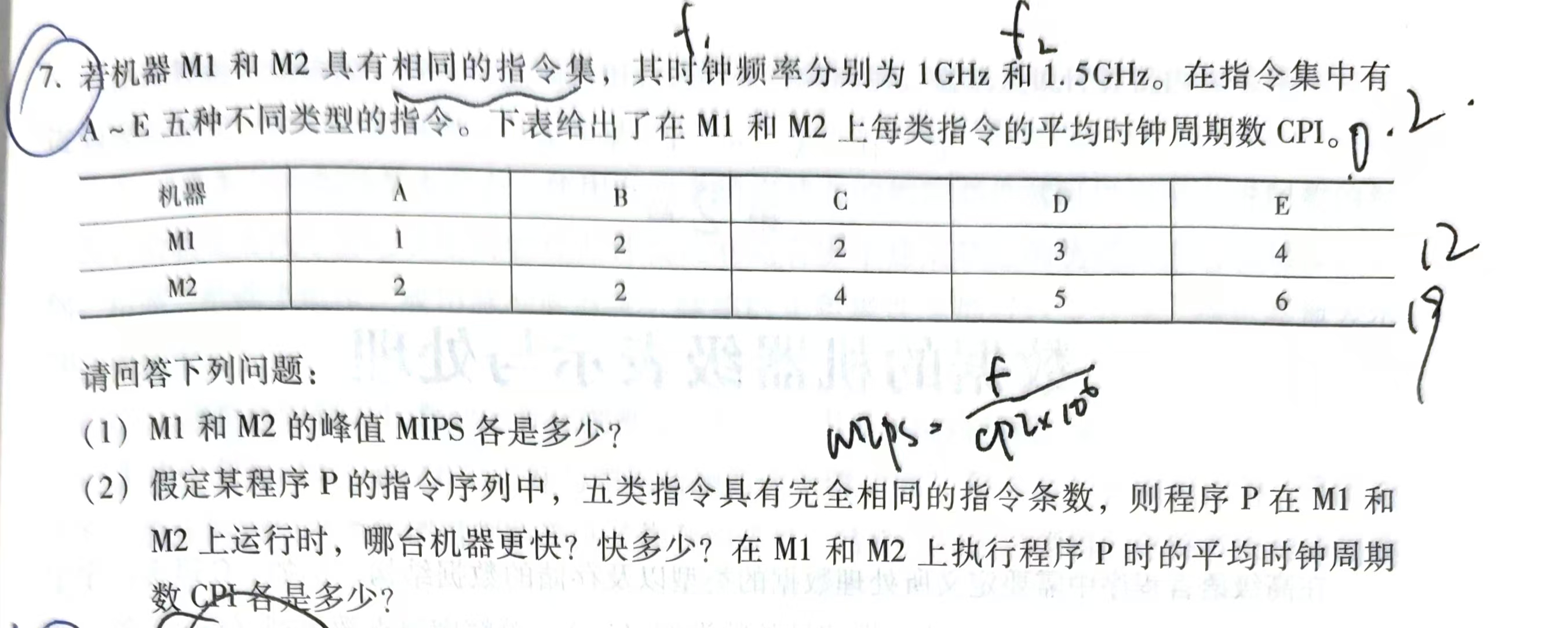
课后习题：6 7 8 10

第二章 数据的机器级表示与处理

信息的二进制编码

机器数：用0和1编码的计算机内部的0/1序列

真值：真正的值，即：现实中带正负号的值

1010-A 1011-B

1100-C 1101-D

1110-E 1111-F

定点数的编码表示

原码

反码：二进制的各位数码取反，符号位表示方法与原码相同

补码：1. 最高位的权重记为-(2^(n-1)) 2. 反码+1

整数的表示及其互相转化

2的16次方：65536

2的15次方：35768

2的31次方：2147483648

C语言标准规定：若运算中同时有无符号和带符号整数，则按无符号整数运算

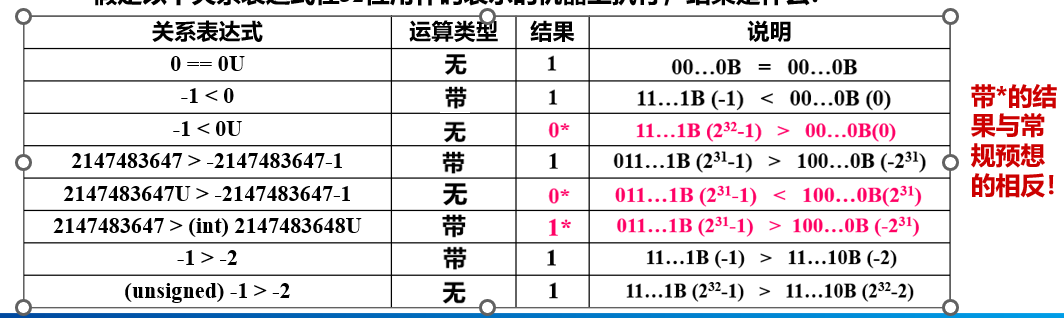
浮点数的表示

浮点数的表示范围

浮点数范围比定点数大，但数的个数没变多，故之间更系数，且不均匀

IEEE754浮点数标准

float（32bit）：1位符号位；8位阶码；23位尾数

符号位：1为负，0为正

阶码：单精度规格化阶码范围为 -126~127 （全0和全1用来表示特殊值）

​ 偏置常数：127

​ 阶码范围：1~254（阶的范围 -126~127）

阶码规定了规格化数的范围：

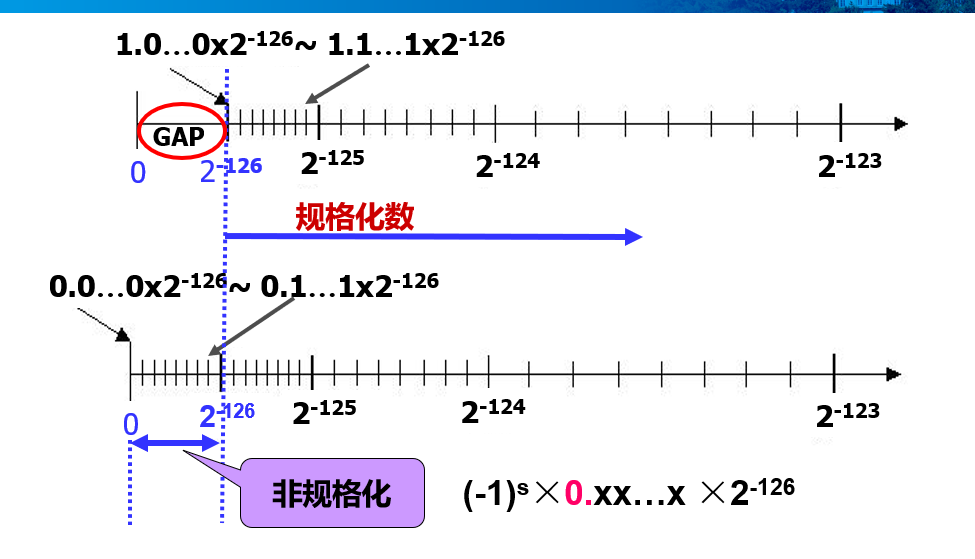
尾数：尾数最高为总是1，所以隐含表示，省一位

double（64bit）：1位符号位，11位阶码；52位尾数

阶码的偏置常数为1023

阶码范围：1_{2046（阶的范围：-1022}1023）

例题

真值转机器数

机器数转真值

特殊数的表示

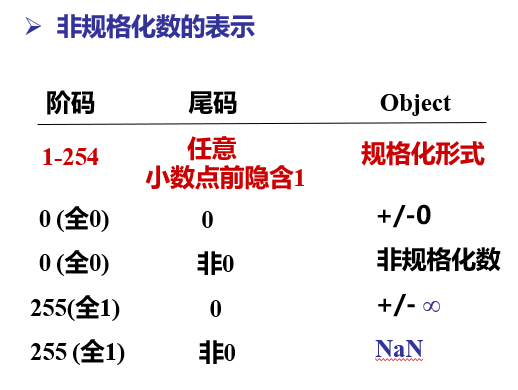
0的机器数表示：阶码全0，尾数全0

无穷的机器数表示：阶码全1（-255），尾数全0

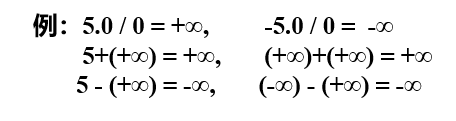
非数表示：阶码全1，尾数非0

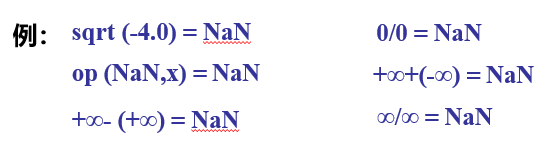
非规格数表示：阶码全0，尾数非0

常用ASCII码

十进制数字：0~9 ASCII码：30H~39H

英文字母：A_Z，az ASCII码：41H（A），61H（a）

空格：20H

回车：0DH

数据的宽度和存储

C语言中数值数据类型的宽度

C声明	32位宽度	64位宽度
char	1	1
short int	2	2
int	4	4
long int	4	8
**char ***	4	8
float	4	4
double	8	8

同类型数据随ISA、机器字长和编译器的不同而不同

\[1~kB = 2^{10}byte = 1024B\\ 1~GB = 2^{30}byte= 1024MB\\ 4~GB = 2^{32}byte \]

（IA-32体系下）

位：1bit

字节：1byte = 8bit

字：1word = 2byte = 16bit

字长：4byte = 32bit

数据的存储和排列顺序

LSB：最低有效位

MSB：最高有效位（一般为符号位）

小端存储就是将数据的最高有效字节存放在大地址单元中（低位在小地址）

大端存储就是将数据的最低有效字节存放在小地址单元中

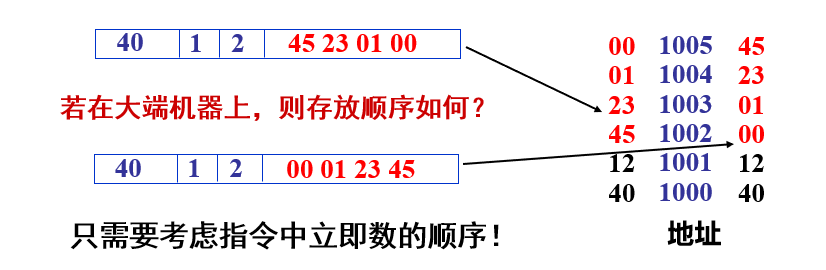
数据的基本运算

按位运算和逻辑运算

逻辑移位：

不考虑符号位。左移：高位移出，低位补0；右移：低位移出，高位补0。对于无符号整数的逻辑左移，如果最高位移出的是1，则发生溢出。

算数移位

左移时：高位移出，低位补0；右移：低位移出，高位补符号位。左移前后符号位不同发生溢出

例题

位拓展运算和位截断运算

用途：类型转换时可能需要数据扩展或截断

操作

1. 没有专门操作运算符，根据类型转换前后数据长短确定是拓展还是截断

2. 拓展：短转长

   ​ 无符号数：0扩展，前面补0
   ​ 带符号整数：符号拓展，前面补符号位

3. 截断：长转短

​ 强行将高位丢弃，故可能发生溢出

例题

整数加减运算

标识寄存器

\[OF = C_n \oplus C_{n-1}\\ CF = C_{out} \oplus C_{in}\\ ZF = 1当且仅当F = 0\\ SF = F_{n-1}\\ (C_{out} = C_{n}， ~~C_n = 加法? 0:1) \]

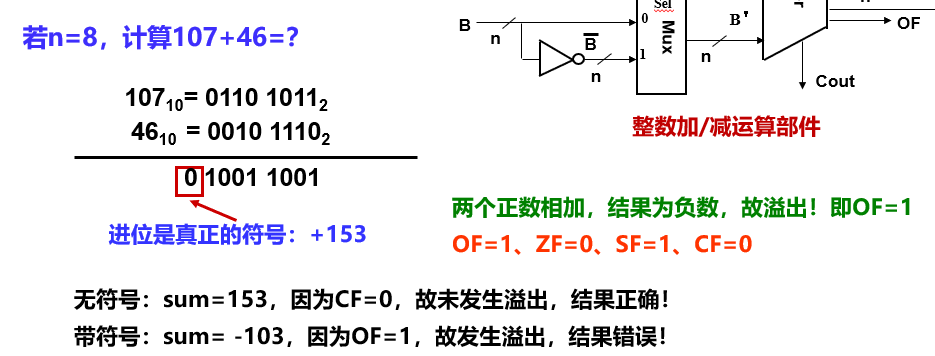
整数加法

无符号溢出：CF = 1

带符号溢出：OF＝1

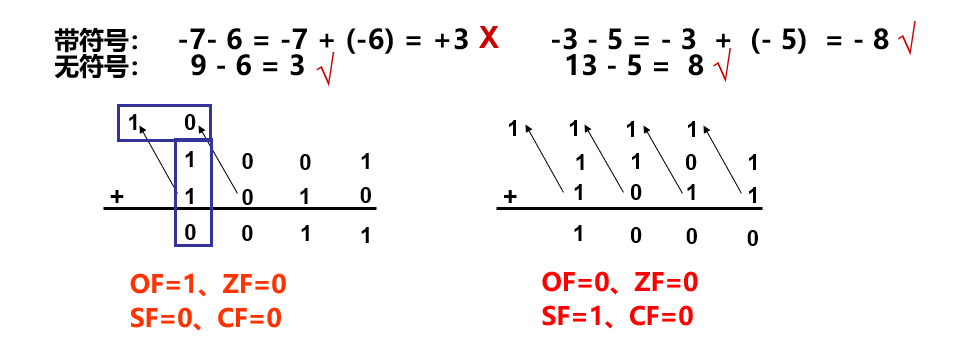
整数减法

无符号溢出：CF = 1

带符号溢出：OF = 1

(x-y)

无符号：CF = 0 => x > y

带符号：OF =SF => x > y

例题

整数乘除运算

整数乘法

通常，高级语言中的两个n位整数相乘得到的结果通常也是一个n位整数。结果只取2n位中的低n位

两个操作数的类型和结果的类型必须一致，如果不一致就先转换成一致的数据类型再进行计算

两个正整数相乘不一定是正数，两个正浮点数相乘则一定是正数

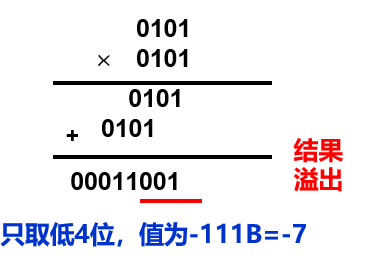
如何判断是否溢出：

无符号：若高n位全0，则不溢出；否则溢出

带符号：若高（n+1）位全0或全1则不溢出

乘法指令不生成溢出标识！

整数除法

除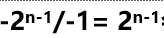会发生溢出外，其余情况都不会发生溢出

整除0的结果无法用一个机器数表示

变量与常数之间的乘除运算

乘法

编译器在处理变量与常数相乘时，往往以移位、加法和减法的组合运算来代替乘法运算。

除法

编译器在处理一个变量与一个2的幂次形式的整数相除时，常采用右移运算来实现。

不能整除时，采用朝零舍入，即截断方式

[!NOTE]

无符号数、带符号正整数（地板）：移出的低位直接丢弃

带符号负整数（天板）：加偏移量(2k-1)，然后再右移k 位 ，低位截断（这里k 是右移位数）

浮点数运算

1. 对阶

​ 小阶向大阶看齐。阶小的那个数尾数右移，右移的尾数等于两个阶的差的绝对值。目的是使两阶码相等

​ 尾数右移的时候，隐含的1移到小数部分，高位补0。移出的低位保持到特定的附加位上

2. 尾数加减

3. 尾数规格化

​

3. 舍入

​ 11：+1

​ 10：进偶

​ 01：0

​ 如果运算结果为0，那么阶码也要为0

浮点数类型转换

int转换为float时，不会发生溢出，但可能有数据被舍入

int或float转换为double时，因为double的有效位数更多，故能保留精确值

double转换为float或int时，可能发生溢出，此外，由于有效位数变少，故可能被舍入

float或double转换为int时，因为int没有小数部分，所以数据可能会向0方向被截断

浮点数运算不满足消去律。或考虑d=1.0, f=-0.1

总结

课后习题：21 22* 23* 28 29 34 35 (41*)

21

22

23

外加：将下列数转化为机器数，并用16进制数表示

int x= -32766 float a =-1.1 float x = 3.3

将下列机器数转换为十进制数

float a = C448 0000H

28

29

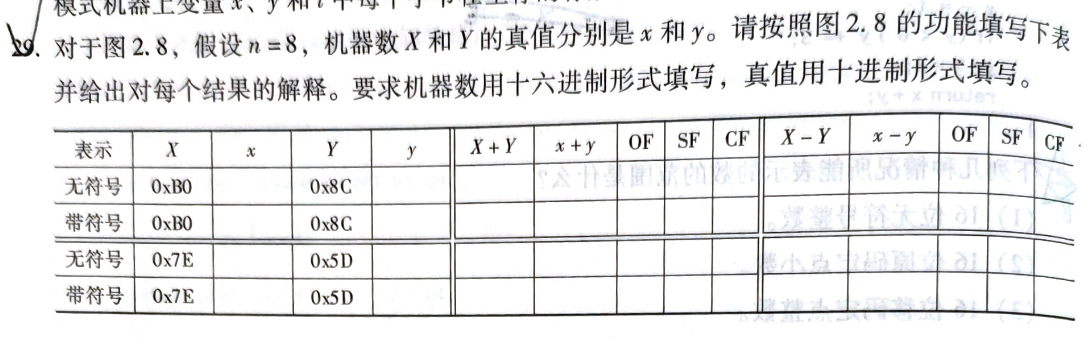
34

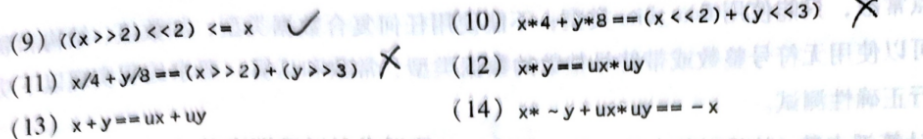
35