P2680 [NOIP2015 提高组] 运输计划 题解
二分答案?数据结构?对不起真不熟,这里给一种不需要二分答案不需要数据结构只需要树上差分和 lca 然后用 set 维护一下最大值而且还好写的做法。
首先注意到我们肯定会将时间最长的 \(s_i\to t_i\) 上面选一条边,否则肯定是不优的(最长的不减剩下的就算为 0 都没用),求这一个上个树上差分即可。
然后有一个显然的结论就是我们可以将路径分成两类,一类包含选择的边,一类不包含选择的边,那么该方案下答案就是两类路径取个最大值(第一类要减去选择边的边权)。
下称 某条路径包含选中边 为 某条路径被这条边断开。
然后考虑将 \(s_i\to t_i\) 这条路径提出来,如图:
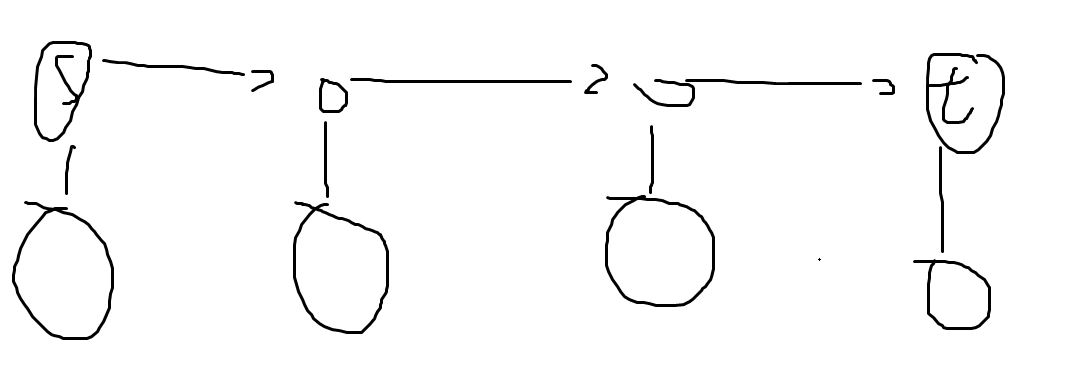
然后我们就知道了哪些边是可能要选的,同时剩下那些没有在路径上的点都会直接或间接的挂在路径上,对这些点染色,颜色就是这个点直接或间接挂上的第一个路径上的点。
于是问题变成了选一条边,按这条边为界,求出所有没有被这条边断开的路径的最大值。
处理是很简单的,对每一条路径染色之后维护 \((l,r)\) 表示这条路径在链上覆盖的区间,从左到右枚举所选的边,此时注意到每条路径只会先被断开一次而后被合回去,于是可以将所有路径按照左端点升序排序就可以用一个指针维护了,至于那些被断开的另外按照右端点升序丢到 set 里面然后同样维护一下即可。求出这个最大值之后再和 提出链的边权和减去当前边的权值 这个值求个最大值,就是选中这条边的最大时间。
然后注意一下就是如果提出的最长链是个点直接输出 0,否则会被卡成 95pts。
这里求最值需要使用 set,因为里面涉及到删除指定数的操作(手写堆当我没说)。
Code:
/*
========= Plozia =========
Author:Plozia
Problem:P2680 [NOIP2015 提高组] 运输计划
Date:2022/11/11
========= Plozia =========
*/
#include <bits/stdc++.h>
typedef long long LL;
using std::multiset;
const int MAXN = 3e5 + 5;
int n, m, Head[MAXN], cntEdge, sum[MAXN], dep[MAXN], Color[MAXN], p[MAXN], fa[MAXN][21], val[MAXN];
bool book[MAXN];
struct EDGE { int To, val, Next; } Edge[MAXN << 1];
struct node { int x, y, t; bool operator <(const node &fir)const { return t > fir.t; } } a[MAXN];
struct SET { int x, id; bool operator <(const SET &fir)const { return x < fir.x; } } ;
multiset <int> Rest; multiset <SET> In;
int Read()
{
int sum = 0, fh = 1; char ch = getchar();
for (; ch < '0' || ch > '9'; ch = getchar()) fh -= (ch == '-') << 1;
for (; ch >= '0' && ch <= '9'; ch = getchar()) sum = (sum << 3) + (sum << 1) + (ch ^ 48);
return sum * fh;
}
void add(int x, int y, int z) { ++cntEdge; Edge[cntEdge] = (EDGE){y, z, Head[x]}; Head[x] = cntEdge; }
bool cmp(const node &fir, const node &sec) { return (Color[fir.x] ^ Color[sec.x]) ? (Color[fir.x] < Color[sec.x]) : (Color[fir.y] < Color[sec.y]); }
void dfs(int now, int f)
{
fa[now][0] = f; dep[now] = dep[f] + 1;
for (int i = Head[now]; i; i = Edge[i].Next)
{
int u = Edge[i].To; if (u == f) continue ;
sum[u] = sum[now] + Edge[i].val; dfs(u, now);
}
}
void init()
{
for (int j = 1; j <= 20; ++j)
for (int i = 1; i <= n; ++i)
fa[i][j] = fa[fa[i][j - 1]][j - 1];
}
int lca(int x, int y)
{
if (dep[x] < dep[y]) std::swap(x, y);
for (int i = 20; i >= 0; --i) if (dep[fa[x][i]] >= dep[y]) x = fa[x][i];
if (x == y) return x;
for (int i = 20; i >= 0; --i) if (fa[x][i] != fa[y][i]) x = fa[x][i], y = fa[y][i];
return fa[x][0];
}
void dfs2(int now, int f, int col)
{
Color[now] = col;
for (int i = Head[now]; i; i = Edge[i].Next)
{
int u = Edge[i].To; if (book[u] || u == f) continue ;
dfs2(u, now, col);
}
}
int main()
{
n = Read(), m = Read();
for (int i = 1; i < n; ++i) { int x = Read(), y = Read(), z = Read(); add(x, y, z); add(y, x, z); }
dfs(1, 1); init();
for (int i = 1; i <= m; ++i)
{
a[i].x = Read(), a[i].y = Read();
a[i].t = sum[a[i].x] + sum[a[i].y] - 2 * sum[lca(a[i].x, a[i].y)];
}
std::sort(a + 1, a + m + 1); if (dep[a[1].x] > dep[a[1].y]) std::swap(a[1].x, a[1].y);
int len = dep[a[1].y] + dep[a[1].x] - 2 * dep[lca(a[1].x, a[1].y)] + 1; int l = lca(a[1].x, a[1].y), cnt = len;
for (int pz = a[1].y; pz != l; pz = fa[pz][0], --cnt) book[p[cnt] = pz] = 1, val[cnt - 1] = sum[pz] - sum[fa[pz][0]];
book[p[cnt] = l] = 1; cnt = 1;
for (int pz = a[1].x; pz != l; pz = fa[pz][0], ++cnt) book[p[cnt] = pz] = 1, val[cnt] = sum[pz] - sum[fa[pz][0]];
for (int i = 1; i <= len; ++i) dfs2(p[i], p[i], i);
for (int i = 2; i <= m; ++i) if (Color[a[i].x] > Color[a[i].y]) std::swap(a[i].x, a[i].y);
std::sort(a + 2, a + m + 1, cmp); l = 2; int ans = 0x7f7f7f7f;
for (int i = 2; i <= m; ++i) Rest.insert(a[i].t);
for (int i = 1; i < len; ++i)
{
while (l <= m && Color[a[l].x] <= i)
{
Rest.erase(Rest.find(a[l].t));
In.insert((SET){Color[a[l].y], l});
++l;
}
while (!In.empty() && (*In.begin()).x <= i)
{
Rest.insert(a[(*In.begin()).id].t);
In.erase(In.begin());
}
if (!Rest.empty()) ans = std::min(ans, std::max(*--Rest.end(), a[1].t - val[i]));
else ans = std::min(ans, a[1].t - val[i]);
}
if (len == 1) { puts("0"); return 0; }
printf("%d\n", ans); return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号