树形dp
HDU 2196 Computer
链接:https://acm.hdu.edu.cn/showproblem.php?pid=2196
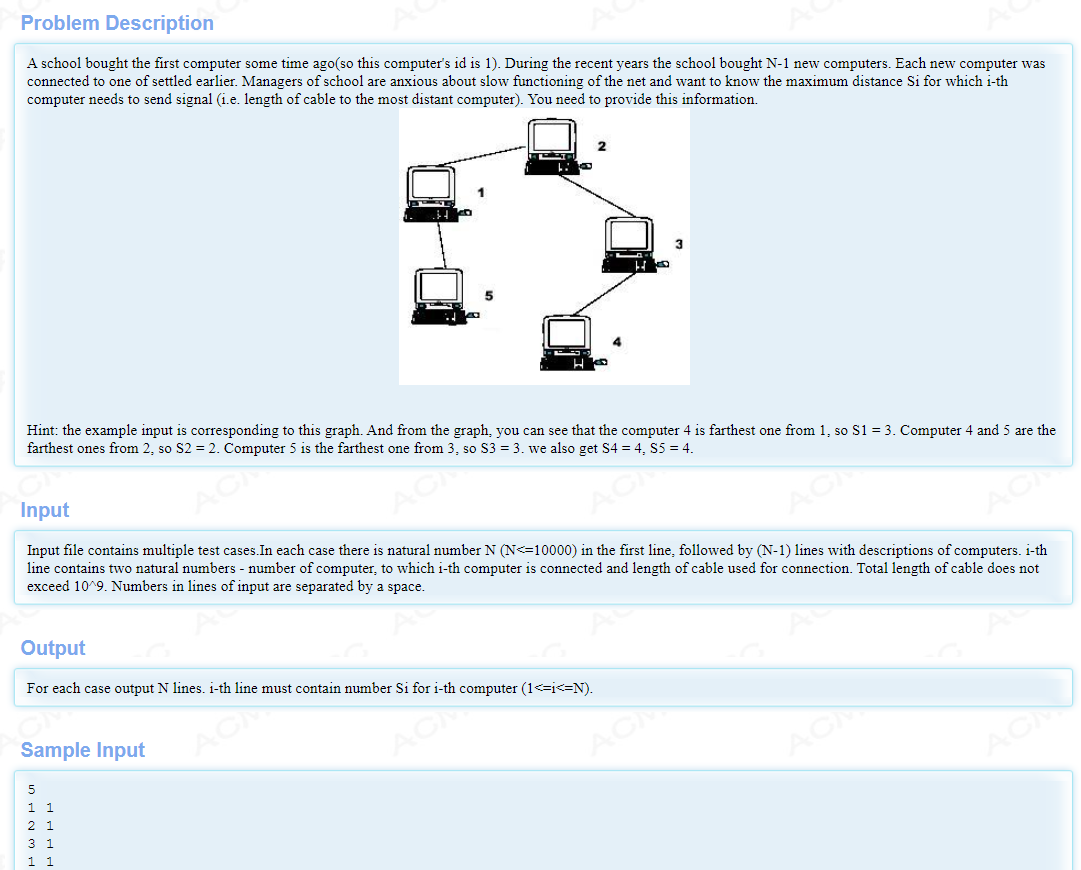
题意:给出一棵树,求离每个节点最远的点的距离
思路:这道题ac后才发现写的麻烦了,下面的代码是认为没有给出根节点来写的,但是实际上题目是给出树根了的,所以建图和处理都麻烦了点
按照无根来写:经典的树形dp,链式前向星存双向边,然后由于是求每个结点到其他结点的最短距离,很容易想到通过求以每个结点作为根节点而形成的子树中根节点到其他结点的最大距离,再通过换根法来逐个求出每个结点的真正的最大距离(树形dp一般都是以结点为划分)
第一遍直接dfs求出每个结点子树的最大距离,第二遍redfs换根求出每个结点的最大值
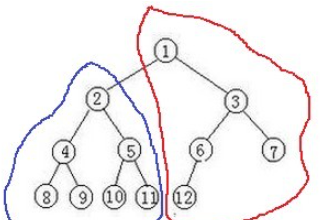
以结点2为例,该结点的最大距离分为两部分,一部分是以2为根节点的蓝色子树的最大距离,另一部分是以2结点的父节点为根节点的子树的最大距离+结点2和父节点的距离
第一部分已经通过第一次dfs求出,第二部分父结点的最大距离可能和2结点形成的子树有关,因此存dfs时存储第一和第二大的最大距离。如果无关,直接使用第一大距离,有关则使用第二大距离来更新当前结点的第一第二大距离值。
代码如下
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <unordered_map>
#include <vector>
using namespace std;
typedef long long LL;
const int N = 1e4+10,M=N<<1,mod=1e9+7;
const double eps=1e-3;
typedef pair<int,int> PII;
#define x first
#define y second
#define sf(a) scanf("%d",&a)
struct Node
{
int a,b,c,d;
};
int h[N],e[M],ne[M],w[M],idx;
void add(int a,int b,int c)
{
e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
PII f[N];
void dfs(int u,int fa)
{
f[u]={0,0};
int &a=f[u].x,&b=f[u].y;
for(int i=h[u];~i;i=ne[i])
{
int to=e[i];
if(to==fa) continue;
dfs(to,u);
int t=f[to].x+w[i];
if(t>a) b=a,a=t;
else if(t==a) b=t;
else b=max(b,t);
}
}
void redfs(int u,int fa,int c)
{
int &a=f[u].x,&b=f[u].y;
if(f[fa].x==f[u].x+c)
{
int t=f[fa].y+c;
if(t>a) b=a,a=t;
else if(t==a) b=a;
else b=max(b,t);
}
else
{
int t=f[fa].x+c;
if(t>a) b=a,a=t;
else if(t==a) b=a;
else b=max(b,t);
}
for(int i=h[u];~i;i=ne[i])
{
int to=e[i];
if(to==fa) continue;
redfs(to,u,w[i]);
}
}
void solve()
{
int n;
while(cin>>n)
{
idx=0;
memset(h,-1,sizeof h);
for(int i=2;i<=n;i++)
{
int a,b;
cin>>a>>b;
add(i,a,b);
add(a,i,b);
}
dfs(1,0);
// for(int i=1;i<=n;i++) cout<<f[i].x<<endl;
redfs(1,1,0);
for(int i=1;i<=n;i++) cout<<f[i].x<<endl;
}
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
// int T;
// cin>>T;
// while(T--)
solve();
}
HDU-6820 Tree
题目链接:https://acm.hdu.edu.cn/showproblem.php?pid=6820
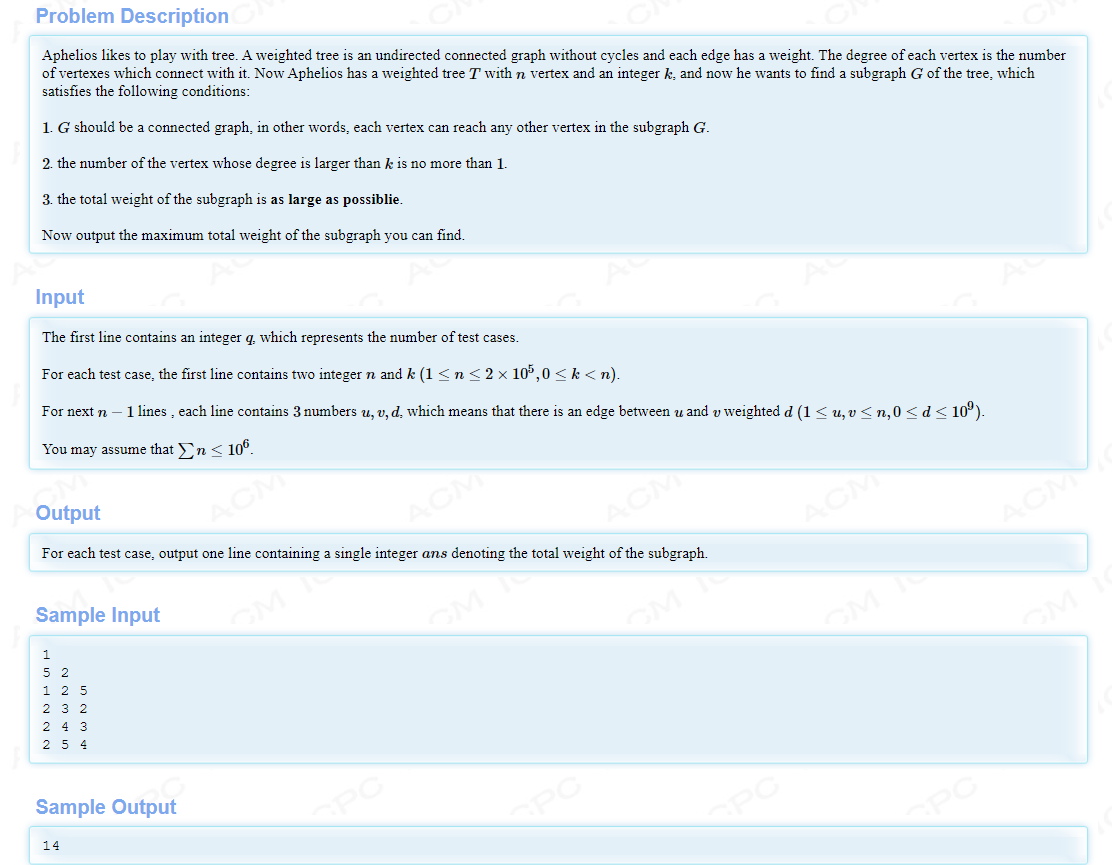
题意:在一个无根树上选择一个的子图,要求子图全联通且度数大于k 的点最多只有1个。问该子图最大的权值。
两种写法:
第一种:状态表示:dp[u][0] 表示以u为根的子图无大于k的点的最大权值。dp[u][1] 表示以u为根的子图有一个大于k的点的最大权值
不多废话,一篇非常好的博客:
https://www.cnblogs.com/A-sc/p/13440370.html
下面是他的代码,我个人加了点注释便于理解
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<map>
#include<queue>
#include<vector>
#include<string>
#include<fstream>
using namespace std;
#define rep(i, a, n) for(int i = a; i <= n; ++ i)
#define per(i, a, n) for(int i = n; i >= a; -- i)
typedef long long ll;
const int N = 2e6 + 105;
const int mod = 998244353;
const double Pi = acos(- 1.0);
const int INF = 0x3f3f3f3f;
const int G = 3, Gi = 332748118;
ll qpow(ll a, ll b) { ll res = 1; while(b){ if(b & 1) res = (res * a) % mod; a = (a * a) % mod; b >>= 1;} return res; }
ll gcd(ll a, ll b) { return b ? gcd(b, a % b) : a; }
//
int n, k;
int head[N], cnt = 0;
ll dp[N][2];
ll res;
struct node{
int to, nxt; ll c;
}edge[N];
void add(int u, int v, ll w){
edge[cnt].to = v, edge[cnt].c = w, edge[cnt].nxt = head[u], head[u] = cnt ++;
edge[cnt].to = u, edge[cnt].c = w, edge[cnt].nxt = head[v], head[v] = cnt ++;
}
bool cmp(int a, int b){
return dp[edge[a].to][0] + edge[a].c > dp[edge[b].to][0] + edge[b].c;
}
void dfs(int u, int pre){
dp[u][0] = dp[u][1] = 0;
vector<int> sol; sol.push_back(0);
int sn = 0; //sonnum;
for(int i = head[u]; i != -1; i = edge[i].nxt){
int v = edge[i].to; ll w = edge[i].c;
if(v == pre) continue;
dfs(v, u);
sol.push_back(i);
sn ++;
}
sort(sol.begin() + 1, sol.begin() + 1 + sn, cmp);
ll maxx1 = 0, maxx2 = 0;
//dp[u][0] and maxx1
for(int i = 1; i <= min(k - 1, sn); ++ i){
int v = edge[sol[i]].to; ll w = edge[sol[i]].c;
dp[u][0] += dp[v][0] + w;
}
//上面表示考虑dp[u][0]的第一种情况pre和u相连
//这是第二种,if代表现在认为pre和u并不相连,那么满足k度就需要再选上第k个结点
if(sn >= k) maxx1 = dp[u][0] + dp[edge[sol[k]].to][0] + edge[sol[k]].c;
else maxx1 = dp[u][0];
res = max(res, maxx1);
// dp[u][1] and maxx2
for(int i = 1; i <= sn; ++ i){
int v = edge[sol[i]].to; ll w = edge[sol[i]].c;
dp[u][1] += dp[v][0] + w;
}
maxx2 = dp[u][1];
for(int i = 1; i <= sn; ++ i){
int v = edge[sol[i]].to; ll w = edge[sol[i]].c;
if(i <= k - 1) dp[u][1] = max(dp[u][1], dp[u][0] - dp[v][0] + dp[v][1]);
else if(k > 1){ //这里表示结点u必须与父结点pre连接的情况
ll mink1 = dp[edge[sol[k - 1]].to][0] + edge[sol[k - 1]].c;
dp[u][1] = max(dp[u][1], dp[u][0] - mink1 + dp[v][1] + w);
}
}
for(int i = 1; i <= sn; ++ i){
int v = edge[sol[i]].to; ll w = edge[sol[i]].c;
if(i <= k) maxx2 = max(maxx2, maxx1 - dp[v][0] + dp[v][1]);
else if(k > 0){ //这里同理,表示结点u必须不与父结点pre连接的情况
ll mink = dp[edge[sol[k]].to][0] + edge[sol[k]].c;
maxx2 = max(maxx2, maxx1 - mink + dp[v][1] + w);
}
}
res = max(res, maxx2);
}
void init(){
cnt = 0;
res = 0;
for(int i = 0; i <= n + 2; ++ i){
head[i] = -1;
dp[i][0] = dp[i][1] = 0;
}
}
int main()
{
int T; scanf("%d",&T);
while(T --){
scanf("%d%d",&n,&k);
init();
for(int i = 1; i < n; ++ i){
int x, y; ll z; scanf("%d%d%lld",&x,&y,&z);
add(x, y, z);
}
if(!k){
printf("0\n");
continue;
}
dfs(1, 0);
printf("%lld\n", res);
}
return 0;
}
第二种:状态表示:dp[i][0]表示第i个位置连向father的最大答案,dp[i][1]表示第i个位置不连向fa的答案
另一篇大佬的博客:https://blog.csdn.net/tianyizhicheng/article/details/107792119
写的和通常做法并不一样,第一次dfs处理认为不存在度数>=k的结点的情况,第二次dfs则是通过枚举每个结点作为唯一度数大于k的结点,通过从父结点向孩子传递未处理当前孩子时已取得的不包含度数>=k的结点的总权值。由于当前孩子作为度数>=k的结点,因此孩子累加其所有孩子的权值,故不用继续向下递归。
#include<bits/stdc++.h>
using namespace std;
int q,n,k;
const int N=2e5+10;
typedef long long ll;
ll ans,dp[N][2];
struct node{
int x;ll v;
bool operator < (const node& a) const
{
return v>a.v;
}
};
vector<node> e[N],vec[N];
void dfs(int u,int f)
{
for(int i=0;i<e[u].size();i++)
{
int v=e[u][i].x;
if(v==f)continue;
dfs(v,u);
vec[u].push_back({v,dp[v][0]+e[u][i].v});//vec里存了所有儿子的dp[v][0]+w(u-v)
}
sort(vec[u].begin(),vec[u].end());
for(int i=0;i<min((int)vec[u].size(),u==1?k:k-1);i++)//如果是根节点,显然dp[u][0]可以选不超过k个儿子,否则只能选不超过k-1个儿子
dp[u][0]+=vec[u][i].v;
for(int i=0;i<min((int)vec[u].size(),k);i++) //不连父结点
dp[u][1]+=vec[u][i].v;
}
void dfs1(int u,int f,ll s)//枚举当前的u点是度数可以超过k的那个点,s代表父亲传下来的贡献,包括u和f之间的边权
{
for(int i=0;i<vec[u].size();i++)
{
int v=vec[u][i].x;
ll w=vec[u][i].v-dp[vec[u][i].x][0];//u-v的边权
if(u==1)
{
if(i>=k)
dfs1(v,u,s+dp[u][0]-vec[u][k-1].v+w);//用v来换掉第k的儿子
else
dfs1(v,u,s+dp[u][0]-dp[vec[u][i].x][0]);//不需要换
}
else
{
if(i>=k)
dfs1(v,u,max(s+dp[u][0]-vec[u][k-2].v+w,dp[u][1]-vec[u][k-1].v+w));//两者的区别在于u有没有连向父亲,所以一个是k-2,一个是k-1
else if(i==k-1)
dfs1(v,u,max(s+dp[u][0]-vec[u][k-2].v+w,dp[u][1]-dp[vec[u][i].x][0]));//第k可以替换掉第k-1,第二种情况是不替换
else
dfs1(v,u,max(s+dp[u][0]-dp[vec[u][i].x][0],dp[u][1]-dp[vec[u][i].x][0]));//不需要替换
}
}
ll sum=0;
for(int i=0;i<vec[u].size();i++)
sum+=vec[u][i].v;
ans=max(ans,sum+s);
}
int main()
{
scanf("%d",&q);
while(q--)
{
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++)
{
e[i].clear();
vec[i].clear();
dp[i][0]=dp[i][1]=0;
}
for(int i=1;i<n;i++)
{
int u,v,d;
scanf("%d%d%d",&u,&v,&d);
e[u].push_back({v,d});
e[v].push_back({u,d});
}
if(k==0)
{
printf("0\n");
continue;
}
ans=0;
if(k==1) //vec里面数组从0开始到k-1结束,由于dfs1里面的else部分,若该结点连接了父结点,则其剩余连接度数减一,故需要替换掉vec[u][k-2],因此k>=2
{
for(int i=1;i<=n;i++)
{
ll sum=0;
for(int j=0;j<e[i].size();j++)
sum+=e[i][j].v;
ans=max(ans,sum);
}
printf("%lld\n",ans);
continue;
}
dfs(1,0);
dfs1(1,0,0);
printf("%lld\n",ans);
}
return 0;
}
HDU 3586 Information Disturbing
题目链接:https://acm.hdu.edu.cn/showproblem.php?pid=3586
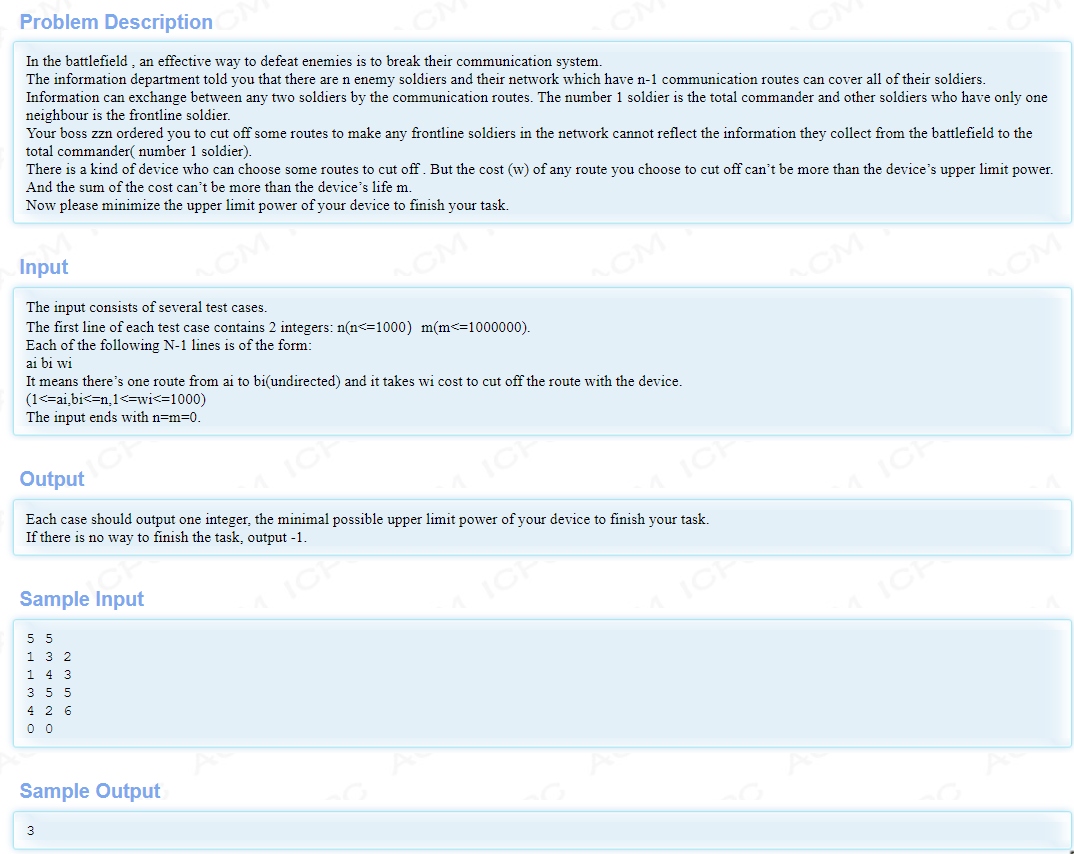
题意:给定n个敌方据点,1为司令部,其他点各有一条边相连构成一棵树,每条边都有一个权值cost表示破坏这条边的费用,叶子节点为前线。现要切断前线和司令部的联系,每次切断边的费用不能超过上限limit,问切断所有前线与司令部联系所花费的总费用少于m时的最小limit。
思路:简单的树形dp,通过二分法来确定limit的值,借助树形dp判断是否合法
这道题被坑了好几个小时,原因没开longlong,白白花了好几个小时找错误,我的评价是:#define int LL
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <unordered_map>
#include <vector>
using namespace std;
typedef long long LL;
const int N = 1e3+10,M=N<<1,mod=1e9+7;
const double eps=1e-3;
const int INF=2e9;
typedef pair<int,int> PII;
#define x first
#define y second
#define sf(a) scanf("%d",&a)
//#define int LL
struct Node
{
int a,b,c,d;
};
int h[N],e[M],ne[M],w[M],idx;
void add(int a,int b,int c)
{
e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
LL f[N];
int n,m;
void dfs(int u,int fa)
{
int flag=0;
LL s=0;
for(int i=h[u];~i;i=ne[i])
{
int to=e[i];
if(to==fa) continue;
dfs(to,u);
flag=1;
LL c=w[i];
if(c>n) s+=f[to];
else s+=min(f[to],c);
}
if(flag)
f[u]=s;
else f[u]=INF;
}
void solve()
{
while(cin>>n>>m,n|m)
{
idx=0;
memset(h,-1,sizeof h);
for(int i=2;i<=n;i++)
{
int a,b,c;
cin>>a>>b>>c;
add(a,b,c);
add(b,a,c);
}
int l=1,r=n;
int res=INF;
while(l<r)
{
int mid=(l+r)>>1;
n=mid;
dfs(1,-1);
if(f[1]<=m) res=mid,r=mid;
else l=mid+1;
}
if(res==INF) cout<<"-1\n";
else
cout<<res<<endl;
}
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
// int T;
// cin>>T;
// while(T--)
solve();
}
POJ 3107 Godfather
题目链接:http://poj.org/problem?id=3107
题意:给出一棵树,求出树的重心,树的重心可能有多个。
思路:记一下最小联通块节点个数,然后对dp扫一遍输出就可以。
代码如下:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
//#include <unordered_map>
#include <vector>
using namespace std;
typedef long long LL;
const int N = 2e6+10,M=N<<1,mod=1e9+7;
const double eps=1e-3;
const int INF=2e9;
typedef pair<int,int> PII;
#define x first
#define y second
#define sf(a) scanf("%d",&a)
//#define int LL
struct Node
{
int a,b,c;
};
int h[M],e[M],ne[M],w[M],idx;
PII f[N];
void add(int a,int b,int c)
{
e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
void add(int a,int b)
{
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void dfs(int u,int fa)
{
int&a=f[u].x;
int&s=f[u].y;
s++;
for(int i=h[u];~i;i=ne[i])
{
int to=e[i];
if(to==fa) continue;
dfs(to,u);
s+=f[to].y;
int t=f[to].y;
if(t>a) a=t;
}
}
void redfs(int u,int fa)
{
int&a=f[u].x;
int&s=f[u].y;
PII t=f[fa];
if(u!=1)
{
a=max(a,t.y-s);
s=t.y;
}
for(int i=h[u];~i;i=ne[i])
{
int to=e[i];
if(to==fa) continue;
redfs(to,u);
}
}
void solve()
{
int n;
cin>>n;
memset(h,-1,sizeof h);
for(int i=1;i<n;i++)
{
int a,b;
cin>>a>>b;
add(a,b);
add(b,a);
}
dfs(1,0);
// for(int i=1;i<=n;i++)
// cout<<f[i].s<<' '<<f[i].x<<' '<<f[i].y<<endl;
redfs(1, 0);
vector<int> res;
int mn=INF;
for(int i=1;i<=n;i++)
{
// cout<<f[i].s<<' '<<f[i].x<<' '<<f[i].y<<endl;
if(mn>f[i].x) mn=f[i].x,res.clear(),res.push_back(i);
else if(mn==f[i].x) res.push_back(i);
}
for(int i=0;i<res.size();i++) cout<<res[i]<<' ';
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
// int T;
// cin>>T;
// while(T--)
solve();
}
POJ 2378 Tree Cutting

题目链接:http://poj.org/problem?id=2378
题意:一棵树,去掉一个点剩下的每棵子树节结点数不超过n/2。问有哪些这样的点,并按照顺序输出。
思路:很容易想到,当删除一个节点p后,会出现:
1.除了以p节点为根的子树的部分,这部分的节点数为n(以p节点为根的子树的节点树)
2.以p节点的每一个孩子为根的子树
如果这些部分全都满足节点数不大于n,那么p节点自然是满足条件的
代码如下:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
//#include <unordered_map>
#include <vector>
using namespace std;
typedef long long LL;
const int N = 2e4+10,M=N<<1,mod=1e9+7;
const double eps=1e-3;
const int INF=2e9;
typedef pair<int,int> PII;
#define x first
#define y second
#define sf(a) scanf("%d",&a)
#define memset(f,a) memset(f,a,sizeof f);
//#define int LL
struct Node
{
int a,b,c;
};
int h[N],e[M],ne[M],w[M],idx;
PII f[N];
void add(int a,int b,int c)
{
e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
void add(int a,int b)
{
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void dfs(int u,int fa)
{
int&a=f[u].x;
int&s=f[u].y;
s++;
for(int i=h[u];~i;i=ne[i])
{
int to=e[i];
if(to==fa) continue;
dfs(to,u);
s+=f[to].y;
int t=f[to].y;
if(t>a) a=t;
}
}
void redfs(int u,int fa)
{
int&a=f[u].x;
int&s=f[u].y;
PII t=f[fa];
if(u!=1)
{
a=max(a,t.y-s);
s=t.y;
}
for(int i=h[u];~i;i=ne[i])
{
int to=e[i];
if(to==fa) continue;
redfs(to,u);
}
}
void solve()
{
int n;
cin>>n;
memset(h,-1);
for(int i=1;i<n;i++)
{
int a,b;
cin>>a>>b;
add(a,b);
add(b,a);
}
dfs(1,0);
redfs(1,0);
vector<int> res;
int t=n/2;
for(int i=1;i<=n;i++) if(f[i].x <=t) res.push_back(i);
if(res.size())
for(int i=0;i<res.size();i++) cout<<res[i]<<endl;
else cout<<"NONE\n";
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
// int T;
// cin>>T;
// while(T--)
solve();
POJ 3140 Contestants Division

题目链接:http://poj.org/problem?id=3140
题意:给你一棵树,让你找一条边,使得两颗子树权值和相差最小,求最小的权值差
思路:直接树形dp,找树权值和sum和2*子树权值和的最小差值就行了
代码如下:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long LL;
const int N = 1e6+10,M=N<<1,mod=1e9+7;
const double eps=1e-3;
const int INF=2e9;
typedef pair<int,int> PII;
#define x first
#define y second
#define sf(a) scanf("%d",&a)
#define int LL
struct Node
{
int a,b,c,d;
};
int n,m;
int a[N];
LL dp[N],minn,sum;
int h[N],e[M],ne[M],w[M],idx;
void add(int a,int b)
{
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void dfs(int u,int fa)
{
dp[u] = a[u];
for(int i = h[u];~i;i =ne[i])
{
int v = e[i];
if(v == fa)
continue;
dfs(v,u);
dp[u] += dp[v];
}
minn = min(minn,(LL)abs(sum-2*dp[u]));
}
void solve()
{
int ca = 0;
while(cin>>n>>m,n|m)
{
idx = 0;
memset(h,-1,sizeof(h));
sum = 0;
for(int i = 1;i <= n;i++)
cin>>a[i],sum += a[i];
while(m--)
{
int a,b;
cin>>a>>b;
add(a,b);
add(b,a);
}
minn = 1e13;
memset(dp,0,sizeof dp);
dfs(1,-1);
cout<<"Case "<<++ca<<": "<<minn<<endl;
}
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
// int T;
// cin>>T;
// while(T--)
solve();
}
POJ 3585 Accumulation Degree

题目链接:http://poj.org/problem?id=3585
题意:找一个点使得,使得从这个点出发作为源点,发出的流量最大,输出这个最大的流量。
思路:先dp一次求出每个点为根的流量最大值。
然后用f[i]表示以i为源点整体流量的最大值,可以发现f[root] = dp[root]
然后考虑访问子节点,假设子节点为u,那么dp[u]肯定是f[u]的一部分,还有一部分就是流向父亲节点所在子树的流量。
在访问该节点前我们如果已知f[s],那么从u流向父亲节点的流量显然就是min(f[s] - min(w(s, u), dp[u]), w(s, u))
注意,如果父亲节点度数为1,需要特判,这时候流量直接就是w(s, u),因为没有别的边有流量流出了
代码如下:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
//#include <unordered_map>
#include <vector>
using namespace std;
typedef long long LL;
const int N = 2e6+10,M=N<<1,mod=1e9+7;
const double eps=1e-3;
const int INF=2e9;
typedef pair<int,int> PII;
#define x first
#define y second
#define sf(a) scanf("%d",&a)
#define mst(f,a) memset(f,a,sizeof f);
#define int LL
struct Node
{
int a,b,c;
};
int h[N],e[M],ne[M],w[M],idx;
int f[N];
int d[N];
void add(int a,int b,int c)
{
e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
void add(int a,int b)
{
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void dfs(int u,int fa)
{
int sc=0;
for(int i=h[u];~i;i=ne[i])
{
int to=e[i];
if(to==fa) continue;
dfs(to,u);
sc+=min(w[i],f[to]==0?w[i]:f[to]); //这里认为叶子结点作为源点无流量,当然也可以设置成正无穷,因为redfs必须要特判叶子结点,所以两者都行
}
f[u]=sc;
}
void redfs(int u,int fa,int c)
{
if(d[fa]==1) f[u]+=c; //这里要特判父结点是否度数为1
else
f[u]+=min((f[fa]-min(c,f[u])),c);
for(int i=h[u];~i;i=ne[i])
{
int to=e[i];
if(to==fa) continue;
redfs(to,u,w[i]);
}
}
void init()
{
idx=0;
mst(h,-1);
mst(d,0);
}
void solve()
{
int n;
cin>>n;
init();
for(int i=1;i<n;i++)
{
int a,b,c;
cin>>a>>b>>c;
add(a,b,c);
add(b,a,c);
d[a]++,d[b]++;
}
dfs(1,0);
// cout<<"dfs\n";for(int i=1;i<=n;i++) cout<<f[i]<<endl;
redfs(1,0,0); //这里第三个参数代表父子之间的路径权值,在处理父节点时必须要写0或者更小数,否则要特判1号结点(因为已经通过dfs求出来了,不用更新)
// cout<<"redfs\n";for(int i=1;i<=n;i++) cout<<f[i]<<endl;
int mx=0;
for(int i=1;i<=n;i++) mx=max(mx,f[i]);
cout<<mx<<endl;
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int T;
cin>>T;
while(T--)
solve();
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号