数位dp
写点数位dp的题
CF300C Beautiful Numbers
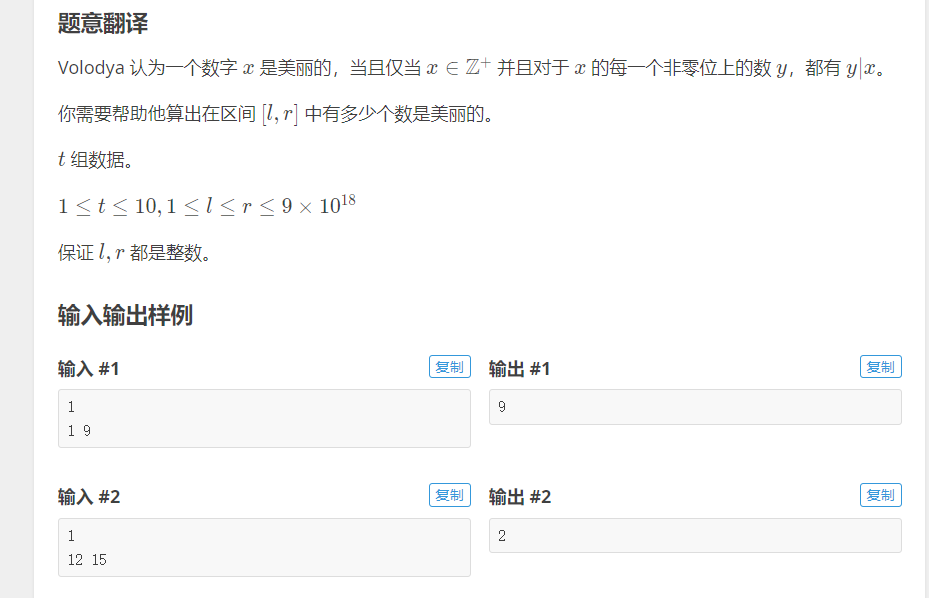
题目链接:https://www.luogu.com.cn/problem/CF55D
思路:数位dp大多都是板子题,这个也是,用记忆化搜索写了
不重复劳动了,补充点不太详细的地方

其中的性质1,很明显,一个数能整除其他数,那这个数一定是最小公倍数的倍数
由于性质2,所有可能出现的k都是2520的因数,借助这一性质,将j取模2520,若所得的结果整除k,那么原来的数也一定整除k。这句话就是2520=t * k(t为倍数),我们原来要判断的就是是否j%k=0,这等价于判断是否j%(t * k)%k=0,所以可以取余
所以可以通过模一个最大的倍数,来将很大的数据限定在一个较小的范围内,并且不影响最大倍数的因数对其取模的结果
最后数组的映射,因为k一定是2520的倍数,而1-2520中很多数不是2520的因数,所以可以直接筛去,来缩小空间
代码如下
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <unordered_map>
using namespace std;
typedef long long LL;
const int N = 2e5+10 ,mod=2520;
const double eps=1e-3;
typedef pair<int,int> PII;
#define x first
#define y second
#define sf(a) scanf("%d",&a)
struct Node
{
int x;
int v;
};
int n;
int d[25];
LL f[25][2530][50];
int a[2540];
int gcd(int a,int b)
{
return b?gcd(b,a%b):a;
}
int lcm(int a,int b)
{
if(a==0) return b;
return a*b/gcd(a,b);
}
LL dfs(int len,int lim,int sum,int minlcm)
{
if(len==0) return sum%minlcm?0:1;
if(~f[len][sum][a[minlcm]]&&!lim) return f[len][sum][a[minlcm]];
int bound=lim?d[len]:9;
LL res=0;
for(int i=0;i<=bound;i++)
res+=dfs(len-1,lim&&i==bound,(sum*10+i)%mod,lcm(i,minlcm));
if(!lim) f[len][sum][a[minlcm]]=res;
return res;
}
LL deal(LL u)
{
int cnt=0;
while(u) d[++cnt]=u%10,u/=10;
return dfs(cnt,1,0,1);
}
void solve()
{
LL l,r;
cin>>l>>r;
cout<<deal(r)-deal(l-1)<<'\n';
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int T;
cin>>T;
memset(f,-1,sizeof f);
int cnt=0;
for(int i=1;i<=mod;i++) if(mod%i==0) a[i]=++cnt;
while(T--)
solve();
}
CF628D Magic Numbers
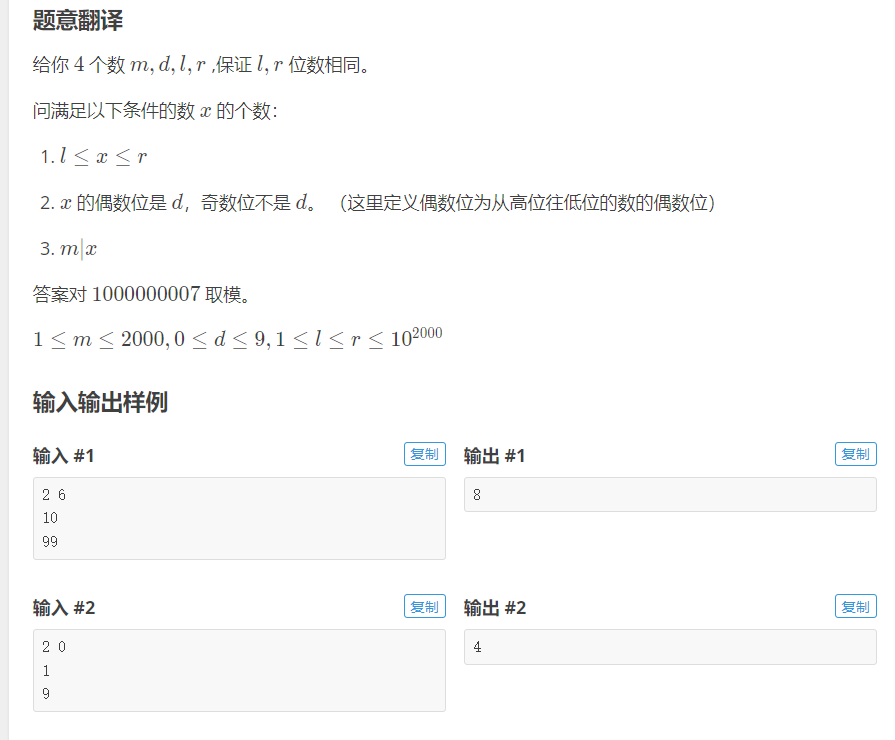
题目链接:https://www.luogu.com.cn/problem/CF628D
思路:套路的数位dp,直接用记忆化搜索,我们传三个参数 len,left,flag 进入 dfs,分别表示枚举到第 len 位,当前数模 m 的余数,以及这一位填的数有没有限制(填d还是不填d),用 f 数组记忆化即可。
这种求数a要满足整除数b的题,和上一题方法是通用的,直接对所求的数模b,最后判断的时候加上条件,只有最后余数为0的才是我们要的答案
这题细节比较多
首先就是10^n就是长度为n+1的字符串
然后注意要翻转一下字符串,这样数位高的才在后面
dfs时记得要注意前导零,到第一位非零数前,flag的类型都是不用变的
f数组也要存储flag,这也是一维区分的条件,由于前导零长度的不同,同一位的flag值可能不同
数位dp求结果一般用的是前缀和,但是这道题如果给l-1,那么还要涉及高精度,所以就所以考虑先计算 [1,r]−[1,l],最后单独判断数 l 是否符合条件
最后,记得memset(f,-1,sizeof f);
代码如下:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <unordered_map>
using namespace std;
typedef long long LL;
const int N = 2000+10 ,mod=1e9+7;
const double eps=1e-3;
typedef pair<int,int> PII;
#define x first
#define y second
#define sf(a) scanf("%d",&a)
struct Node
{
int x;
int v;
};
LL f[N][N][2];
//LL deal(LL u)
//{
// int cnt=0;
// while(u) d[++cnt]=u%10,u/=10;
// return dfs(cnt,1,3);
//}
int m,d;
char l[N],r[N];
int sz;
LL dfs(char* s ,int len,int lim,int lead,int left,int flag)
{
if(!len)
{
if(!lead&&!left) return 1;
return 0;
}
if(~f[len][left][flag]&&!lim&&!lead) return f[len][left][flag];
int bound=lim?s[len]-'0':9;
LL res=0;
if(lead)
{
res+=dfs(s,len-1,0,1,0,1);
res%=mod;
for(int i=1;i<=bound;i++)
{
if(i==d) continue;
res+=dfs(s,len-1,lim&&i==bound,0,(left*10+i)%m,flag^1);
res%=mod;
}
}
else
{
if(flag)
for(int i=0;i<=bound;i++)
{
if(i==d) continue;
res+=dfs(s,len-1,lim&&i==bound,0,(left*10+i)%m,flag^1);
}
else if(d<=bound) res+=dfs(s,len-1,lim&&d==bound,0,(left*10+d)%m,flag^1),res%=mod;
}
if(!lim&&!lead) f[len][left][flag]=res%mod;
return res;
}
int check(char*s)
{
int flag=1;
LL num=0;
for(int i=sz;i;i--)
{
if(flag&&s[i]-'0'==d) return 0;
else if(!flag&&s[i]-'0'!=d) return 0;
flag^=1;
num=(num*10+s[i]-'0')%m;
}
if(num) return 0;
return 1;
}
void solve()
{
cin>>m>>d;
cin>>l+1>>r+1;
sz=strlen(l+1);
reverse(l+1,l+1+sz);
reverse(r+1,r+1+sz);
cout<<((-dfs(l,sz,1,1,0,1)+dfs(r,sz,1,1,0,1)+check(l))%mod+mod)%mod<<'\n';
// cout<<dfs(l,llen,1,1,0,1)<<' '<<dfs(r,rlen,1,1,0,1)<<' '<<check(l)<<'\n';
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
// int T;
// cin>>T;
memset(f,-1,sizeof f);
// while(T--)
solve();
}
这道题有点难,先放着以后再补
CF809C Find a car
题目链接:https://www.luogu.com.cn/problem/CF809C
Tachibana Kanade's Tofu
ac自动机+数位dp
题目链接:https://www.luogu.com.cn/problem/CF433E
Fox and Perfect Sets
线性基
题目链接:https://www.luogu.com.cn/problem/CF388D
New Year and Original Order
题目链接:https://www.luogu.com.cn/problem/CF908G


 浙公网安备 33010602011771号
浙公网安备 33010602011771号