区间dp
练习一下区间dp,总结一下不会的题型,当做笔记
括号配对问题 Brackets Sequence
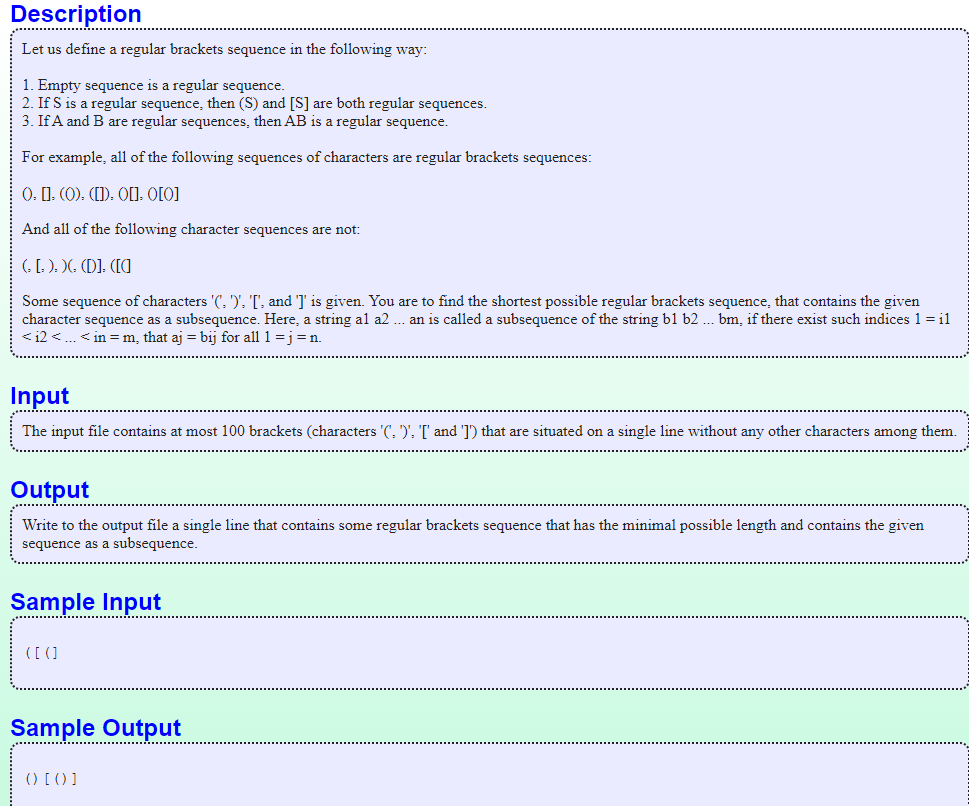
链接:http://poj.org/problem?id=1141
题意:给一串括号序列。依照合法括号的定义,加入若干括号,使得序列合法。
一道典题,思路是括号配对加上路径回溯,找出输入的所有不配对单括号,在输出时将其补充成完整括号对即可
括号配对
求序列配对的括号量,使用三层循环,前两层枚举长度和起点,然后要注意括号配对时更新dp值。由于合法的括号对都是嵌套或者并列的,所以第三层的枚举中间点只能帮我们解决括号的并列,但是不能解决括号的嵌套,所以我们还要自己加入判断,即当该区间的左右端点括号匹配时,dp[l][r]=dp[l+1][r-1]+1。
路径回溯
这个也是典型,有两种方法,一种是不开辟数组,通过原来的dp转移方程来递归,另一种是开一个数组(一般dp过程可以简化数组维度,但路径回溯不可以,不过少部分题也可以),这个数组用来记录前驱(就是由谁更新了它),然后层层访问前驱即可。
以前写背包的路径回溯,两种方法都比较简单,现在看区间dp,感觉第二种好用点。区间dp由于第三层循环的存在,所以两种方法都会麻烦一点,第一种得遍历中间点,第二种得递归左区间和右区间。
代码:
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 1e2+10 , M = N<<1,mod=1e9+7;
typedef long long LL;
typedef pair<int,int> PII;
//#define x first
//#define y second
//int h[N],e[M],ne[M],idx;
//
//void add(int a,int b)
//{
// e[idx]=b,ne[idx]=h[a],h[a]=idx++;
//}
struct Node
{
int l1,r1;
int l2,r2;
};
char s[N];
int f[N][N];
Node path[N][N];
int st[N];
void dfs(int l,int r) //路径回溯
{
Node t =path[l][r];
if(t.l1==l+1&&t.r1==r-1)
{
st[l]=st[r]=1;
dfs(l+1,r-1);
}
else if((t.l1|t.l2|t.r1|t.r2)==0) return; //记得要加边界条件
else
{
dfs(t.l1,t.r1);
dfs(t.l2,t.r2);
}
}
int check(int l,int r) //检查括号是否匹配
{
if(s[l]=='('&&s[r]==')'||s[l]=='['&&s[r]==']') return 1;
return 0;
}
void deal(char c) //补全括号
{
if(c=='('||c==')') cout<<"()";
else if(c=='['||c==']') cout<<"[]";
}
void solve() //区间dp
{
cin>>s+1;
int size=strlen(s+1);
for(int len=2;len<=size;len++)
for(int r=len;r<=size;r++)
{
int l=r-len+1;
if(check(l,r)) //额外的判断条件
{
Node& t =path[l][r];
if(f[l][r]<f[l+1][r-1]+1) f[l][r]=f[l+1][r-1]+1,t.l1=l+1,t.r1=r-1;
}
for(int k=l;k<r;k++)
{
Node& t =path[l][r];
int sum=f[l][k]+f[k+1][r];
if(sum>f[l][r])
{
f[l][r]=sum;
t.l1=l,t.r1=k;
t.l2=k+1,t.r2=r;
}
}
}
dfs(1,size);
for(int i=1;i<=size;i++)
{
if(!st[i]) deal(s[i]);
else cout<<s[i];
}
cout<<'\n';
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
// int T;
// cin>>T;
// while(T--)
solve();
}
乡村邮局问题-Post Office(POJ-1160)
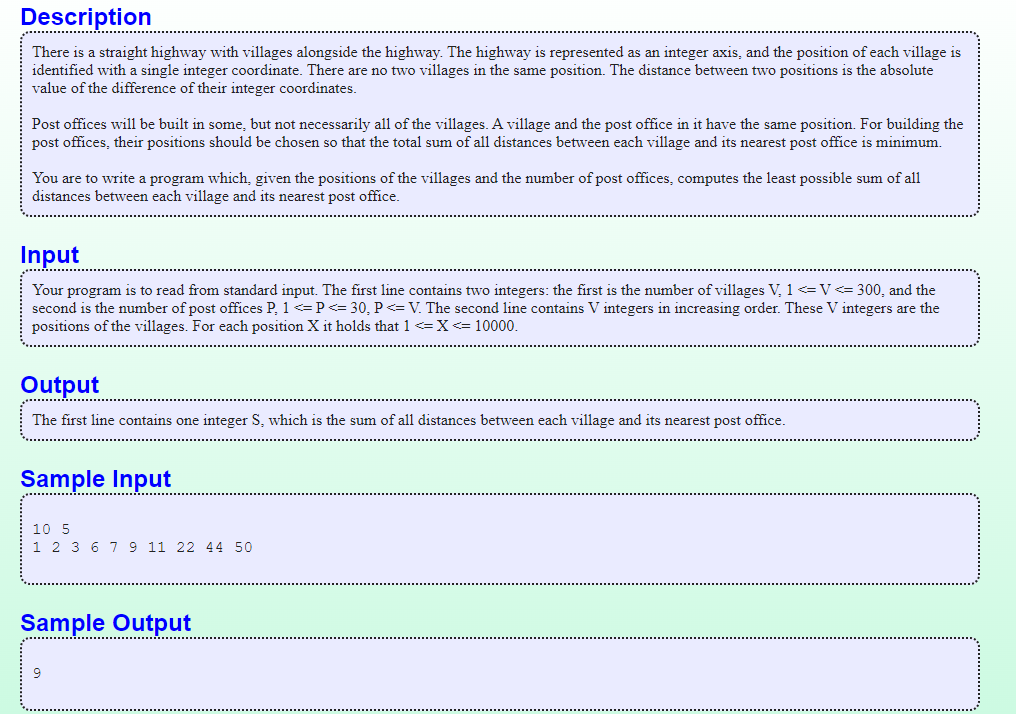
链接:http://poj.org/problem?id=1160
题意:在一个水平坐标轴上有V个村子,每个村子的位置上都可以建一座邮局,一共有P个邮局,问V个村子P个邮局的建造方案中,村子到邮局的最短距离和为多少。(只要求距离,不需要把具体方案输出来)。
这个题其实我感觉有点像线性dp。。。
思路:我们可以轻松的知道一定范围内的村子中建造一个邮局的最短距离和,那我们以此为突破口。一定村子内建一个邮局等效于在n个点中找其中一点,使得所有点到它的总和距离最小。这个是个结论,n是奇数那么取中点,n为偶数取最中间两点任意一点均可(若可以取线段上一点,则这个点还可以取在中间两点间)。由此,可以直接求出n个村子到一个邮局的距离总和。
所以我们要进行划分,将前n个村子划分为一组(它们已达最优),将剩下取的m个村子划分为距下一个邮局最近的一组(也达到最优),这样就可以直接求出m个村子的距离总和(一会解释方法)。
接下来直接dp求解即可:f[i][j]=min(f[i][j],f[k][j-1]+dis(k+1,i));
dp可以是前n个村子放m个邮局,也可以是m个邮局放前n个村子。
两种方法都会提供
代码如下:
前n个村子放m个邮局
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 3e2+10 , M = N<<1,mod=1e9+7;
typedef long long LL;
typedef pair<int,int> PII;
//#define x first
//#define y second
//int h[N],e[M],ne[M],idx;
//
//void add(int a,int b)
//{
// e[idx]=b,ne[idx]=h[a],h[a]=idx++;
//}
struct Node
{
int l1,r1;
int l2,r2;
};
int f[N][35];
int a[N];
int dis(int l,int r)
{
int d=0;
while(l<r)
{
d+=a[r]-a[l];
r--;
l++;
}
return d;
}
void solve() //前n个村子放m个邮局
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
memset(f,0x3f,sizeof f);
f[0][0]=0;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=min(m,i);j++)
{
for(int k=0;k<i;k++)
f[i][j]=min(f[i][j],f[k][j-1]+dis(k+1,i));
}
}
// for(int i=1;i<=n;i++)
// {
// for(int j=1;j<=min(m,i);j++) printf("%-5d",f[i][j]);
// puts("");
// }
cout<<f[n][m];
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
// int T;
// cin>>T;
// while(T--)
solve();
}
m个邮局放前n个村子
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 3e2+10 , M = N<<1,mod=1e9+7;
typedef long long LL;
typedef pair<int,int> PII;
//#define x first
//#define y second
struct Node
{
int l1,r1;
int l2,r2;
};
int f[35][N];
int a[N];
int dis(int l,int r)
{
int d=0;
while(l<r)
{
d+=a[r]-a[l];
r--;
l++;
}
return d;
}
void solve() //m个邮局放前n个村子
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i];
memset(f,0x3f,sizeof f);
f[0][0]=0;
for(int i=1;i<=m;i++)
for(int j=i;j<=n;j++)
{
for(int k=i-1;k<j;k++)
f[i][j]=min(f[i][j],f[i-1][k]+dis(k+1,j));
}
// for(int i=1;i<=n;i++)
// {
// for(int j=1;j<=min(m,i);j++) printf("%-5d",f[i][j]);
// puts("");
// }
cout<<f[m][n];
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0);
// int T;
// cin>>T;
// while(T--)
solve();
}
注意的问题:这个当时初始化出错了,方法要不就是想dp意义初始化,如f[0][0]=0 ,0邮局0村子,距离和为0 ;要不就是手动算一下都要用到哪些状态,初始化前面的
讲一下求n个点距离总和最短的方法:
我写的是直接遍历,很容易发现:假设已经选出了最优点,那么n个点到它的距离,其实就是n/2个左右配对的端点的距离差之和,我就是这样遍历的
这里有一个预处理n个点打表做的
int main()
{
int vnum, pnum;
cin >> vnum >> pnum;
int dp[310][40];//dp[a][b]存放 1到a的村子(前a个村子) 设置b个邮局的 最短距离和。
int v[1000];//存放村庄位置
int bdis[310][310];//bdis[a][b]存放从a--b的村子之间存放一个邮局的最短距离和,为最基础的距离和(basic distance),是dp循环的基础元
for (int i = 1; i <= vnum; i++) {
cin >> v[i];
}
memset(bdis, 0, sizeof(bdis));
memset(dp, 0, sizeof(dp));//初始化dp数组为0,主要为初始化dp[a][b]中a=b的情况,即村庄数与邮局数相等,必然是距离和为0
for (int i = 1; i <= vnum; i++)
{
for (int j = i + 1; j <= vnum; j++)
{
bdis[i][j] = bdis[i][j - 1] + v[j] - v[(i + j) / 2];//利用迭代求出bdis的值(当村庄数为偶数时,邮局设置在偏左的中心和偏右的中心并不影响最短距离,所以直接加上v[j] - v[(i + j) / 2]即可)
if (i == 1) {
dp[j][1] = bdis[i][j];//初始化dp[a][b]中b为1的情况,即前a个村子只有一座邮局的情况(由于是前a个村子,所以bdis[i][j]的i必须为1)
}
// cout << "bdis " << bdis[i][j] << endl;
}
}
for (int j = 2; j <= pnum; j++) {//j为设置多少邮局,由于j为1时前一循环已经初始化(只有一座邮局的情况),所以j从2开始(至少两座邮局)
for (int i = j + 1; i <= vnum; i++) {//i为村子数,至少要为j,但ij相等的情况已经初始化为0,所以i从j+1开始
dp[i][j] = 0x3f3f3f3f;
for (int k = j - 1; k < i; k++) {//循环k,即前k村设置j-1个邮局( dp[k][j - 1]),后面k+1到i的村子设置1个邮局(bdis[k + 1][i]),与原dp[i][j]比较得到最小dp
dp[i][j] = min(dp[i][j], dp[k][j - 1] + bdis[k + 1][i]);
}
}
}
cout << dp[vnum][pnum] << endl;
return 0;
}
回文串区间dp [USACO07OPEN]便宜的回文Cheapest Palindrome
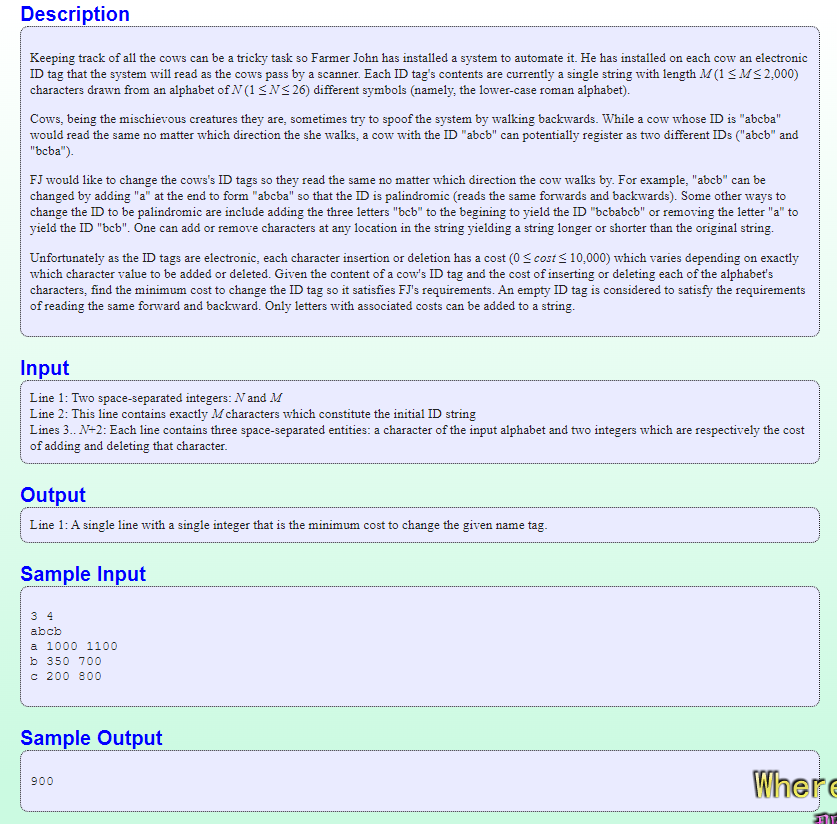
题目链接:http://poj.org/problem?id=3280
题意:输入一个只包含英文小写字母的字符串,再输入所有用到的字符的添加代价,删除代价。输出将这个字符串变为回文串的最小代价。
思路:首先是删除代价和添加代价处理 对于一个字符串,想要将它变为一个回文串,在修改过程中,其实删除字符和添加字符是等效的。举个例子 adba 变为回文串 ,可以删除d变为aba,也可以添加d到对应位置变为adbda,两者操作不同,但是效果是相同的,都变成了回文串。所以数据处理时,直接保留删除和添加字符代价最小的操作即可。
接下来是dp分析。这个题是通法,大部分回文题都可以套。对于一个字符串(假设已经求出将其变为回文串的最小代价),我们可以发现,当它在任意一端增加一个字符时,会出现两种情况:
1、左右两端字符相同,则不用处理两端,那么这个新串的最小代价就等同于去掉它左右两端各一个字符的串的最小代价。
2、左右两端字符不同,鉴于旧串已处理过,已经是回文串,那么想要将新串变为旧串,就是增删那个新加入的字符(分为左端点修改和右端点修改)
所以dp状态表示 集合:从l到r的字符串变为回文串的最小代价 属性:最小值
转移方程:if(s[l]==s[r]) f[l][r]=f[l+1][r-1];
f[l][r]=min(f[l][r],f[l+1][r]+h[s[l]]); 左端点修改
f[l][r]=min(f[l][r],f[l][r-1]+h[s[r]]); 右端点修改
也可以参考这个解释:

代码如下:
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
typedef long long LL;
const int N = 2010;
char s[N];
int h[200];
int f[N][N];
void solve()
{
int n,m;
cin>>n>>m;
cin>>s+1;
for(int i=0;i<n;i++)
{
char a;
int b,c;
cin>>a>>b>>c;
h[a]=min(b,c);
}
for(int len=2;len<=m;len++)
for(int r=len;r<=m;r++)
{
int l=r-len+1;
if(s[l]==s[r]) f[l][r]=f[l+1][r-1];
else
{
f[l][r]=0x3f3f3f3f;
f[l][r]=min(f[l][r],f[l+1][r]+h[s[l]]);
f[l][r]=min(f[l][r],f[l][r-1]+h[s[r]]);
}
}
cout<<f[1][m];
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
// int T;
// cin>>T;
// while(T--)
solve();
}
CodeForces - 1025D: Recovering BST 二叉搜索树区间dp模拟建树
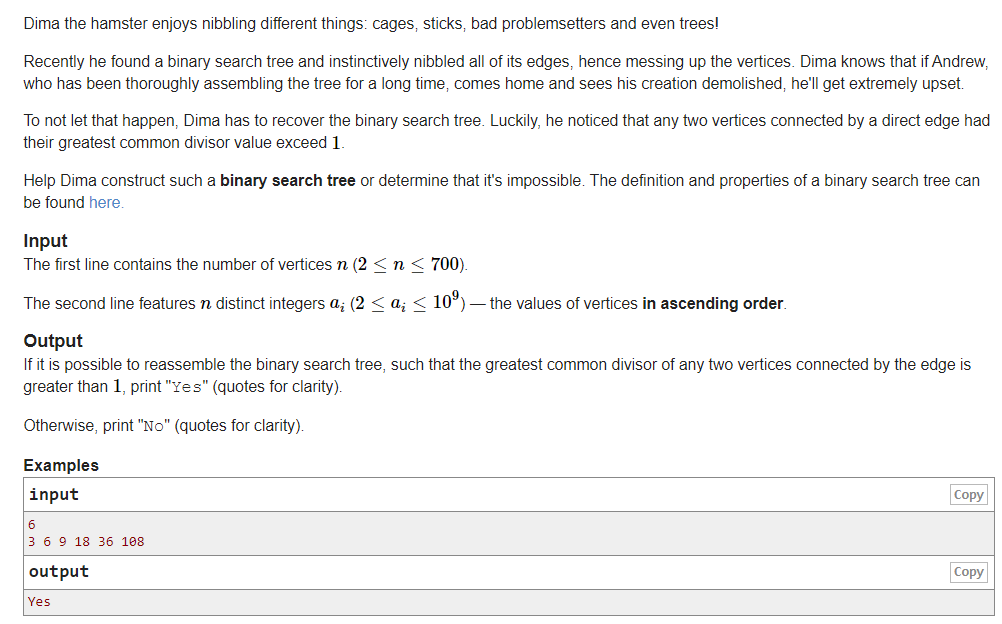
题目链接:https://codeforces.com/problemset/problem/1025/D
题意:给定一个升序序列,如果两个数gcd不为1,则可以连边,现在问连边是否可以构造二叉搜索树(左子树的节点值都小于本节点,右子数都大于)。
思路:如果没注意到二叉搜索树这一条件,这题绝对做不出来!!!
二叉搜索树的定义是,对同一节点,左儿子权值比它小,右儿子权值比它大。 于是有一个很重要的性质,中序遍历上点权从小到大。
可以得出推论:
一棵子树(在中序遍历上可视为一段区间[l,r][l,r]),把它作为左儿子,根结点的父亲一定为r+1;把它作为右儿子,根节点父亲一定为l-1。
如果直接暴力枚举的话,设状态表示为f[l][r][k][2],表示以k为根,[i,j]作为其左/右儿子是否合法,但是这会MLE和TLE(On^4),所以需要进行优化
下面贴一个自己看懂了的解释

拓展的区间就是,现在[l,r]已经处理完毕,根节点为k,那么它可能是l-1的右孩子,也有可能是r+1的左孩子,因此要扩展转移标记。
还有一个点就是要优化一下两个数的gcd,打表优化,否则会超时
代码如下:
其中L[N],R[N]分别代表作为一个结点的左孩子和右孩子是否可行,含义同贴图
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
typedef long long LL;
const int N = 710;
typedef pair<int,int> PII;
#define x first
#define y second
int a[N];
int f[N][N];
int L[N][N];
int R[N][N];
int deal[N][N];
int gcd(int a,int b)
{
return b?gcd(b,a%b):a;
}
void solve()
{
int n;
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i],L[i][i]=R[i][i]=1;
for(int i=1;i<=n;i++) for(int j=i;j<=n;j++) if(gcd(a[i],a[j])>1) deal[i][j]=deal[j][i]=1;
for(int len=1;len<=n;len++)
for(int r=len;r<=n;r++)
{
int l=r-len+1;
for(int k=l;k<=r;k++)
{
if(L[l][k]&&R[k][r])
{
if(l==1&&r==n)
{
puts("Yes");
return;
}
if(deal[l-1][k]) R[l-1][r]=1;
if(deal[r+1][k]) L[l][r+1]=1;
}
}
}
puts("No");
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
// int T;
// cin>>T;
// while(T--)
solve();
}
hdu 1966 /poj 2066 Minimax Triangulation 计算几何

题目链接:http://poj.org/problem?id=2066
题意:给你n个点围成的多边形,顺时针或者逆时针给你,起始点任意,让你把他划成n-2个三角形,这些划法中最大的三角形的面积最小,输出这个最小值。
思路:这个题我真是吐了,被坑了好久,WA了一堆,一点点试才改过去的。本身这个题是个水题,但是还是有一点要注意的
以前做过类似的题,不过那个题的多边形是凸多边形,也就是不会有点凹进去,而这个题没有规定,所以要考虑出现凹进去的情况
先来考虑凸多边形:我们在多边形上随便取三点连接构成三角形,可以发现,这个三角形将图形分隔成三部分(由于连线之间不可相交),一部分是该三角形,剩下两部分是两个多边形,这样问题就得到了简化。取三角形其中任意一边(一般按顺序取)作为我们划分的依据,dp[l][r]代表所有将(l,l+1),(l+1,l+2)···(r-1,r),(r,l)这个多边形划分成三角形的方案中三角形的最大最小值。
分割方式: 选择起点和终点构成的那条边,然后从剩余的点中选择一点构成三角形,这种分割方式可以保证分割后的两个多边形也是由连续的点构成的
我们可以很容易得到转移方程 dp[l][r]=min(dp[l][r],max(dp[l][k],dp[k][r]));
由于这是一个环,可能有人想要破环成链,但是其实是不用的,因为这个dp其实是一个链式dp,由于多边形上的每一条边都在某一个三角形中,所以无论从哪里作为起点开始都是可以的。
然后让我们回到本题,本题并没有规定多边形为凸多边形,这就会产生一个问题,我们l,r,k划分出来的多边形,内部可能包含其他的点
画了个草图,左边是凸多边形,直接连就行,右边d点凹了进去,连接abc三点时,就会把并不存在的bc边连接上,导致内部多出一个d点,不符合题目要求
检查的方法很简单,就是遍历除abc三点以外的所有点,如果存在某个点(设为d),面积abd+acd+bcd=abc,就证明它是内部点,不符
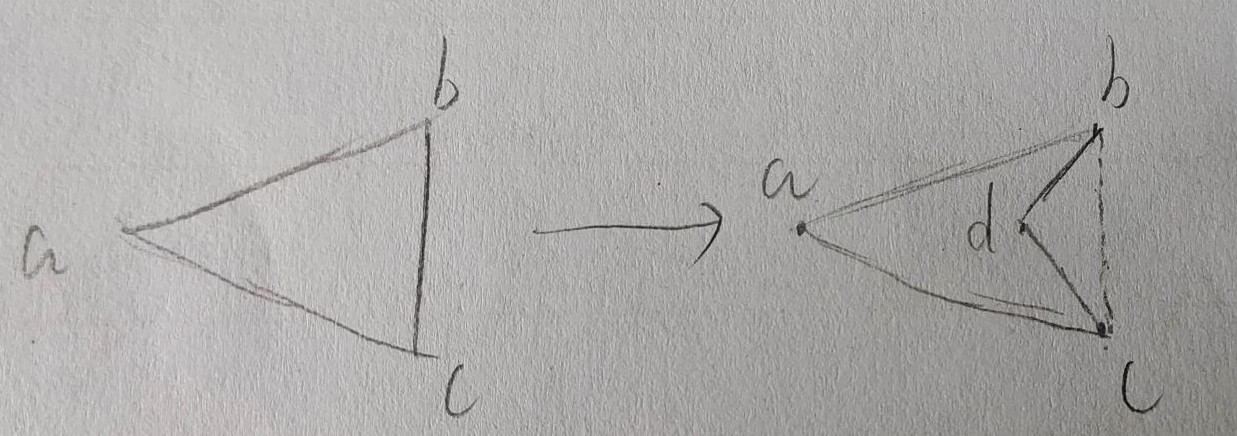
这是涉及三角形的判断

所以在状态转移时,多加一个判断过滤这种情况就好
本题涉及了三角形面积公式,是一个板子,直接贴图

最后就是printf输出double类型要用%f,我用%lf错了n发。。。
代码如下
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 55;
typedef pair<int,int> PII;
#define x first
#define y second
#define sf(a) scanf("%d",&a)
const double eps=1e-3;
double f[N][N];
PII da[N];
int n;
int mul(int a,int b)
{
return da[a].x*da[b].y-da[a].y*da[b].x;
// return a.x*b.y-a.y*b.x;
}
double calc(int a,int b,int c)
{
return 1.0/2*abs(mul(a,b)+mul(b,c)+mul(c,a));
// int ret=mul(a,b)+mul(b,c)+mul(c,a);
// if(ret>0)
// return ret/2.0;
// else
// return -ret/2.0;
}
int check(int a,int b,int c)
{
double s=calc(a,b,c);
for(int i=1;i<=n;i++)
{
if(i==a||i==b||i==c) continue;
if( fabs(
calc(a,b,i)
+calc(i,b,c)
+calc(a,i,c)
-s)<eps)
return 0;
}
return 1;
}
void solve()
{
cin>>n;
for(int i=1;i<=n;i++)
{
int a,b;
scanf("%d%d",&a,&b);
da[i]=make_pair(a,b);
}
// memset(f,0,sizeof f);
// for(int i=1;i<=n-2;i++) f[i][i+2]=calc(i,i+1,i+2);
//
// for(int len=3;len<n;len++)
// for(int l=1;l+len<=n;l++)
// {
// int r=l+len;
// f[l][r]=2e9;
// for(int k=l+1;k<r;k++)
// if(check(l,r,k)) f[l][r]=min(f[l][r],max(calc(l,r,k),max(f[l][k],f[k][r])));
// }
//
for(int len=3;len<=n;len++)
{
for(int r=len;r<=n;r++)
{
int l=r-len+1;
f[l][r]=2e9;
for(int k=l+1;k<r;k++)
{
if(check(l,r,k))
f[l][r]=min(f[l][r],
max(
f[l][k],max(f[k][r],calc(l,r,k) )
)
);
}
}
}
printf("%.1f\n",f[1][n]);
}
int main()
{
// ios::sync_with_stdio(0);
// cin.tie(0);
// cout.tie(0);
int T;
scanf("%d",&T);
while(T--)
solve();
}
CF1107E Vasya and Binary String
题目链接:https://codeforces.com/problemset/problem/1107/E
题意:给定一个 0101 串,消除一段长度为 i 的全 0 或全 1 串获得分值\(a_i\),求将这个串消除完的最大分数
思路:


就是区间左端点第一个字符,要不和前面的字符一起被删去,要不和前面的相同字符合并(不删去),并等待下一个相同字符。
dp[l][r][k] 即代表 l······l l~r
------------------共k个l
当然,以左端点或者右端点为基准做这道题都是可以的
另外,本题有一点要注意:分值数组每个长度的分值不一定会最优的,应该通过前面的长度拼凑进行优化(当然本题dp不用)

代码如下
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 110;
const double eps=1e-3;
typedef pair<int,int> PII;
#define x first
#define y second
#define sf(a) scanf("%d",&a)
char s[N];
int a[N];
LL f[N][N][N];
void solve()
{
int n;
cin>>n;
cin>>s+1;
for(int i=1;i<=n;i++) cin>>a[i];
// for(int i=2;i<=n;i++)
// for(int j=1;j<i;j++) a[i]=max(a[i],a[i-j]+a[j]);
for(int len=1;len<=n;len++)
{
for(int r=len;r<=n;r++)
{
int l=r-len+1;
for(int k=0;k<l;k++)
{
f[l][r][k]=a[k+1]+f[l+1][r][0];
for(int i=l+1;i<=r;i++)
{
if(s[i]==s[l]) f[l][r][k]=max(f[l][r][k],f[i][r][k+1]+f[l+1][i-1][0]);
}
}
}
}
// for(int i=1;i<=n;i++)
// {
// for(int j=1;j<=n;j++) printf("%-5lld",f[i][j]);
// puts("");
// }
cout<<f[1][n][0];
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
// int T;
// scanf("%d",&T);
// while(T--)
solve();
}
codefroces 1198D Rectangle Painting 1
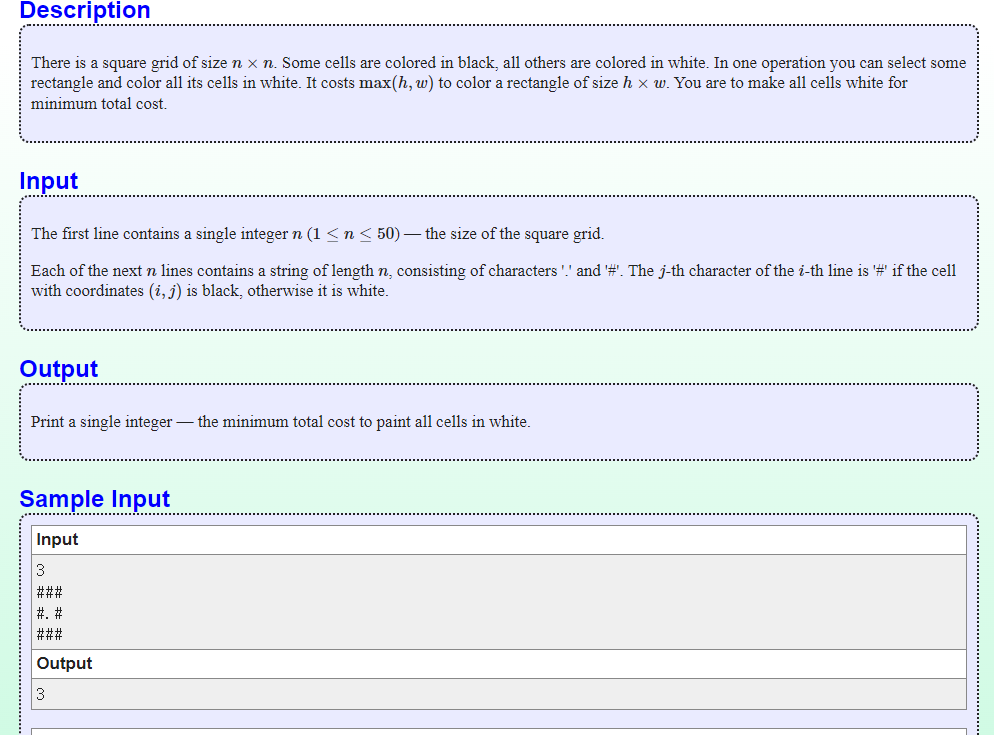
题目链接:https://codeforces.com/problemset/problem/1199/F
题意:给一个棋盘,有黑色的棋子和白色的棋子,把一个宽为w高为h的矩形内的棋子染成白色的代价为max(h,w),问把所有的黑色棋子染成白色的最小代价。
思路:简单的二维区间dp,dp[i][j][x][y]表示把以(i,j)作为左上角,(x,y)作为右下角的矩阵染成白色的最小代价,那么对于一个矩形,要么直接染成白色,要么把它切成两部分(竖着切或者横着切),再递归的计算两部分的代价。
代码如下:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 55;
const double eps=1e-3;
typedef pair<int,int> PII;
#define x first
#define y second
#define sf(a) scanf("%d",&a)
int f[N][N][N][N];
char s[N][N];
void solve()
{
int n;
cin>>n;
for(int i=1;i<=n;i++) cin>>s[i]+1;
for(int len1=1;len1<=n;len1++) //行
for(int r2=len1;r2<=n;r2++)
{
int r1=r2-len1+1;
for(int len2=1;len2<=n;len2++) //列
for(int l2=len2;l2<=n;l2++)
{
int l1=l2-len2+1;
if(len1==1&&len2==1)
{
f[l1][r1][l2][r2]=s[l1][r1]=='#';
continue;
}
int res=max(len1,len2);
for(int k=l1;k<l2;k++) res=min(res,f[l1][r1][k][r2]+f[k+1][r1][l2][r2]);
for(int k=r1;k<r2;k++) res=min(res,f[l1][r1][l2][k]+f[l1][k+1][l2][r2]);
f[l1][r1][l2][r2]=res;
}
}
cout<<f[1][1][n][n];
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
// int T;
// scanf("%d",&T);
// while(T--)
solve();
}
CF1312E Array Shrinking

题目链接:https://codeforces.com/contest/1312/problem/E
题意:给定一个数组,定义一次合并为对于两个相邻的数\(a_i\)、\(a_i+1\),如果他们相等,则可以将它们合并为一个数,其值为\(a_i\)+1。问原数组合并完后的最小长度。
思路:


总的来说就是开两个dp[i][j]数组,一个来存区间合并长度最小值,一个来存合并过程中哪些区间是被缩成一个数的。
代码如下
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 505;
const double eps=1e-3;
typedef pair<int,int> PII;
#define x first
#define y second
#define sf(a) scanf("%d",&a)
struct Node
{
int x;
int v;
};
int a[N];
Node f[N][N];
void solve()
{
int n;
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int len=1;len<=n;len++)
for(int r=len;r<=n;r++)
{
int l=r-len+1;
if(len==1)
{
f[l][r]={a[l],1};
continue;
}
f[l][r].v=2e9;
for(int k=l;k<r;k++)
{
f[l][r].v=min(f[l][k].v+f[k+1][r].v,f[l][r].v);
if(f[l][k].x&&f[k+1][r].x&&f[l][k].x==f[k+1][r].x) f[l][r].x=f[l][k].x+1,f[l][r].v=1;
}
}
cout<<f[1][n].v;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
// int T;
// scanf("%d",&T);
// while(T--)
solve();
}

CF1372E Omkar and Last Floor

题目链接:https://www.luogu.com.cn/problem/CF1372E
思路:

这是另一个解释

这个是对定义状态dp[l][r]的解释

接下来提一下\(S_{i,j,k}\)(以下简称为S)的计算,前面的题解感觉解释的不够
S的求解:(1)最普通的是直接for枚举,由于S代表的左右端点都在区间内且经过了 k 这个位置的区间数量,所以当读取区间(l,r)时,为l~r的所有点都保存其所在的区间,for枚举时判断其左右端点是否都在区间内即可
下面两种是优化的(O(n^3))
(2)第一种是差分优化
直接贴代码
int main()
{
read( N ), read( M );
for( int i = 1 ; i <= N ; i ++ )
{
int K, l, r;
read( K );
while( K -- )
{
read( l ), read( r );
for( int a = 1 ; a <= l ; a ++ )
for( int b = r ; b <= M ; b ++ )
su[a][b][l] ++, su[a][b][r + 1] --;
}
}
for( int i = 1 ; i <= M ; i ++ )
for( int j = i + 1 ; j <= M ; j ++ )
for( int k = i ; k <= j ; k ++ )
su[i][j][k] += su[i][j][k - 1];
for( int i = M ; i ; i -- )
{
f[i][i + 1] = -INF;
for( int j = i ; j <= M ; j ++ )
for( int k = i ; k <= j ; k ++ )
f[i][j] = MAX( f[i][j], f[i][k - 1] + f[k + 1][j] + su[i][j][k] * su[i][j][k] );
}
write( f[1][M] ), putchar( '\n' );
return 0;
}
su是预处理数组
当读取第i行的一段[a,b]时,由于S求的是左右端点都在区间内且经过了 k 这个位置的区间数量,所以只要区间包住了[a,b],那么一定符合这个条件
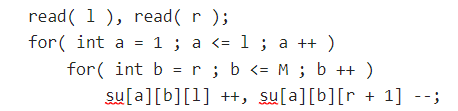
所以[l,r]都要加1,进行差分
所有区间都差分完毕后,进行前缀和求和,求出每个区间的S,最后直接用就可以了
(3)第二种是前缀和
代码如下
signed main()
{
read(n); read(m);
for(int i = 1; i <= n; ++i) {
read(len[i]);
for(int j = 1; j <= len[i]; ++j) {
int x, y; read(x); read(y);
for(int k = x; k <= y; ++k)
++s[k][x][y];
}
}
for(int k = 1; k <= m; ++k) {
for(int l = m; l; --l)
for(int r = 1; r <= m; ++r)
s[k][l][r] += s[k][l][r-1];
for(int l = m; l; --l)
for(int r = 1; r <= m; ++r)
s[k][l][r] += s[k][l+1][r];
}
for(int k = 1; k <= m; ++k) f[k][k] = s[k][k][k] * s[k][k][k];
for(int len = 1; len < m; ++len)
for(int i = 1; i + len <= m; ++i) {
int j = i + len;
for(int k = i; k <= j; ++k) f[i][j] = Max(f[i][j], f[i][k-1] + s[k][i][j] * s[k][i][j] + f[k+1][j]);
}
printf("%d\n", f[1][m]);
return 0;
}
读取一个区间后,直接将区间l~r均加一
然后进行前缀和求解
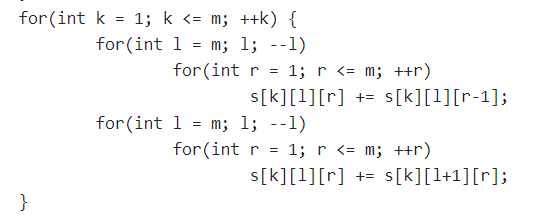
因为小区间一定包含在大区间中,所以从小区间开始向左右两端扩展
未优化的代码如下(O(n^4))
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 110 ,mod=1;
const double eps=1e-3;
typedef pair<int,int> PII;
#define x first
#define y second
#define sf(a) scanf("%d",&a)
struct Node
{
int x;
int v;
};
LL f[N][N];
PII range[N][N];
void solve()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
{
int k;
cin>>k;
for(int p=0;p<k;p++)
{
int a,b;
cin>>a>>b;
for(int j=a;j<=b;j++) range[i][j]={a,b};
}
}
for(int len=1;len<=m;len++)
for(int r=len;r<=m;r++)
{
int l=r-len+1;
for(int k=l;k<=r;k++)
{
int cnt=0;
for(int i=1;i<=n;i++) if(range[i][k].x>=l&&range[i][k].y<=r) cnt++;
f[l][r]=max(f[l][r],f[l][k-1]+f[k+1][r]+cnt*cnt);
}
}
cout<<f[1][m];
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
// int T;
// scanf("%d",&T);
// while(T--)
solve();
}
CF149D Coloring Brackets
推荐直接看题解:
https://www.luogu.com.cn/problem/solution/CF149D
CF607B Zuma
题目链接:https://www.luogu.com.cn/problem/CF607B
思路:这个也是回文串区间dp,和前面写的一样套板子就好

注意如果a[l]==a[r],当区间长度仅为2时要特判处理,f[l][r]应该为1,而不是等于f[l+1][r-1]=0
另外还要注意,上面这个判断和下面的枚举断点是不冲突的,两者都要进行判断,不能使用if...else
代码如下:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 510 ,mod=1000000007;
const double eps=1e-3;
typedef pair<int,int> PII;
#define x first
#define y second
#define sf(a) scanf("%d",&a)
struct Node
{
int x;
int v;
};
int a[N];
int f[N][N];
void solve()
{
int n;
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int len=1;len<=n;len++)
for(int r=len;r<=n;r++)
{
int l=r-len+1;
if(len==1)
{
f[l][r]=1;
continue;
}
f[l][r]=2e9;
if(a[l]==a[r])
{
f[l][r]=f[l+1][r-1];
if(l+1==r) f[l][r]=1;
}
for(int k=l;k<r;k++)
f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]);
}
// for(int i=1;i<=n;i++)
// {
// for(int j=1;j<=n;j++) printf("%-5d",f[i][j]);
// puts("");
// }
cout<<f[1][n];
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
// int T;
// scanf("%d",&T);
// while(T--)
solve();
}
放两道题有机会补:
CF1336C Kaavi and Magic Spell
CF321E Ciel and Gondolas



 浙公网安备 33010602011771号
浙公网安备 33010602011771号