CF506E Mr. Kitayuta's Gift（字符串，矩阵-快速幂，DP，DFA，*）

CF506E Mr. Kitayuta's Gift

字符串 \(s\) 中插入恰好 \(n\) 个小写字符产生的不同回文串数。\(|s| \le 200\)，\(n \le 10 ^ 9\)。模 \(10 ^ 4 + 7\)。

CODE

首先设 \(n + |s|\) 是偶数，最终结果字符串是 \(S\)。

DP 设 \(f(i, l, r)\) 表示 \(S\) 的前 / 后 \(i\) 个字符与 \(s\) 两端尽量匹配还剩下 \([l, r]\) 未匹配。容易写出转移。

对 \(l, r\) 两维压缩 DFA：\(s_l = s_r\) 的是绿点，否则是红点。

初始 DFA：

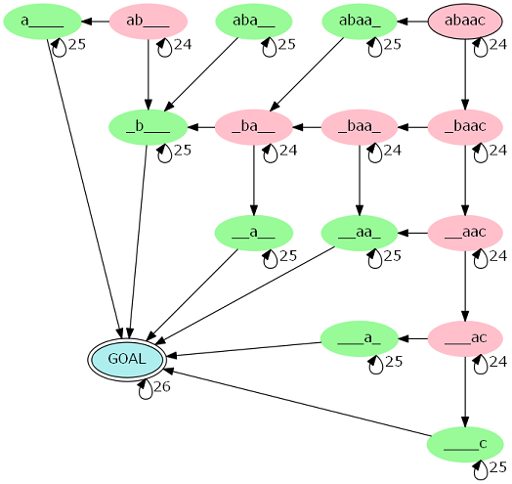
重要的只有路径的红 / 绿点个数。可以根据起点（abaac）到终点（GOAL）每条路径的转移规律，压缩 DFA：

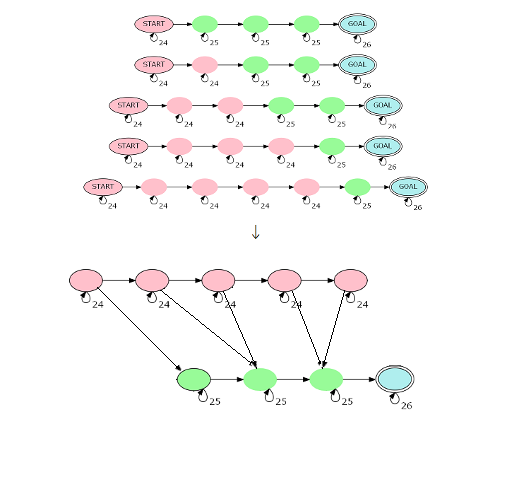
在转移矩阵的 红点到绿点方案数上 还有矩阵快速幂的 base 中最左绿点（即 \(s\) 本身就是回文串时才会有值 \(1\)）附上原 DFA 中这样的路径的数量。

这个路径数用 DP 算，设 \(g(l, r, k)\) 表示还剩 \([l, r]\) 没有匹配，已经用了 \(k\) 次非 \(s_l = s_r\) 两边一起消操作的方案数。转移不提。

如果 \(n + |s|\) 是奇数就减去 最后一步正好在 \(S\) 中间那个字符从 __aa__ 这样的绿点转移过来的方案数 \(X\)。

求 \(X\) 用求答案案类似的方法，调整一下转移矩阵即可。