格初步（六）

The Subset-Sum Problem 子集和问题

我们首先回顾子集和问题（有时也称为“背包”问题）在其搜索形式下的定义。

定义 1 子集和问题

给定正整数权重 (\mathbf{a} = (a_1, \ldots, a_n))，以及
[
s = \sum_{i=1}^n a_i x_i = \langle \mathbf{a}, \mathbf{x} \rangle \in \mathbb{Z}
]
对于某些比特 (x_i \in {0, 1})，求解 (\mathbf{x} = (x_1, \ldots, x_n))。

\(P\) 问题：能在多项式时间内被确定性算法解决的问题。
\(NP\) 问题：解的正确性可在多项式时间内验证的问题。
\(NP\) 完全问题：\(NP\) 中最难的问题，满足两个条件：\(1\). 属于 \(NP\) 类; \(2\). 所有 \(NP\) 问题均可多项式归约到它。意义：若某个 \(NP\) 完全问题存在多项式时间算法，则所有 \(NP\) 问题均可在多项式时间内解决（即 \(P=NP\) ）
\(NP\) 难问题：至少与 \(NP\) 完全问题一样困难的问题，满足：\(1\). 所有 \(NP\) 问题均可多项式归约到它；\(2\). 不要求属于 \(NP\) 类。

在这个求解过程中我们称 \((\mathbf{a},s)\) 为一个待求解的子集和实例（ subset-sum instance）。

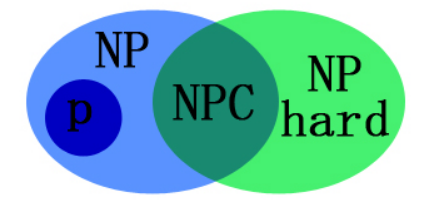
子集和问题（在其自然的判定版本中）是 \(NP\) 完全的。然而，请注意 \(NP\) 完全性是一个最坏情况下的概念，即，似乎不存在能同时高效地解决每一个子集和实例的算法。至于“多数实例”是否可以高效求解，以及“多数实例”具体指什么，则是另一个问题。正如下文所示，某些“结构化的”子集和实例是可以轻易求解的。此外，我们还将看到，如果 (a_i) 的比特长度相对于 (n) 足够大，那么对于几乎所有的 (\mathbf{a})，利用 \(\mathrm{LLL}\) 算法可以轻易求解子集和问题。

Knapsack Cryptography 背包密码

受子集和问题的简单性和 NP 完全性的启发，20 世纪 70 年代末，有人提出将其作为公钥加密方案的基础；参见 [Odl90] 的综述。在这些系统中，公钥由从某个指定分布中选取的权重 (\mathbf{a} = (a_1, \ldots, a_n)) 组成，而加密消息 (\mathbf{x} \in {0,1}^n) 的方法是计算密文：

[
s = \operatorname{Enc}_{\mathbf{a}}(\mathbf{x}) = \langle \mathbf{a}, \mathbf{x} \rangle
]

这种加密算法的一个主要优点是其高效性：加密只需对 (n) 个整数求和，远比其他密码系统中使用的模幂运算等操作要快得多。至于安全性，从密文中恢复消息 \(\mathbf{x}\) 等价于求解子集和实例 \((\mathbf{a}, s)\) ，而我们希望这个问题是困难的。

这里所指的困难性是指恢复消息的困难性。不过公认的加密安全性概念要求的远不止是恢复整个消息的困难性。然而，这种困难性显然是必要的：如果消息对于窃听者来说确实容易恢复，那么该加密方案就是不安全的。

当然，生成公钥的接收方必须能够恢复消息，即解密密文。这通过在权重中嵌入一个秘密的“陷门”实现，从而允许接收方将密文转换为另一个容易求解的子集和实例。

一类容易求解的子集和实例涉及以下类型的权重。

定义 2 超递增序列

一个超递增序列 (\mathbf{a} = (a_1, \ldots, a_n)) 是满足对所有 (i)，都有 (a_i > \sum_{j=1}^{i-1} a_j) 的序列。

给定任意一个超递增序列 (\mathbf{a}) 和 (s = \langle \mathbf{a}, \mathbf{x} \rangle)，求解 (\mathbf{x}) 是容易的：观察到当且仅当 (s > \sum_{j=1}^{n-1} a_j) 时，(x_n = 1)。在求得 (x_n) 后，可以递归地求解实例 ((\mathbf{a}' = (a_1, \ldots, a_{n-1}), s' = s - a_n x_n))，其中 (\mathbf{a}') 仍是超递增序列。

当然，我们不能直接将超递增序列作为公钥，否则窃听者也可以轻易解密。最终的构想是将超递增序列嵌入到一个“看似随机”的公钥中，并附带一个陷门，使得我们可以将后者还原为前者。Merkle 和 Hellman 在 [MH78] 中提出的原始方法是：对权重进行置换，并用一个随机秘密乘数模另一个随机模数进行乘法变换，如下所示：

\(1\). 从某个超递增序列 (\mathbf{b} = (b_1, \ldots, b_n)) 开始；
\(2\). 选择一个模数 (m > \sum_{i=1}^n b_i)，一个均匀随机的乘数 (w \in \mathbb{Z}m^*)，以及一个 ({1, \ldots, n}) 上的均匀随机置换 (\pi)；
\(3\). 令 (a_i = w \cdot b \bmod m)。公钥为 (\mathbf{a} = (a_1, \ldots, a_n))，陷门为 ((m, w, \pi))。

对消息 (\mathbf{x} \in {0,1}^n) 的加密为：

[
s = \operatorname{Enc}{\mathbf{a}}(\mathbf{x}) = \langle \mathbf{a}, \mathbf{x} \rangle = w \cdot \sum^n b_{\pi(i)} x_i \bmod m
]

给定陷门 ((m, w, \pi))，我们可以如下解密 (s)：直接计算

[
s' := w^{-1} s = \sum_{i=1}^n b_{\pi(i)} x_i \bmod m
]

然后对置换后的超递增序列 (\mathbf{b}) 和 (s') 解子集和问题。这是可行的，因为 (\sum_{i=1}^n b_{\pi(i)} x_i < m)，所以 (s') 实际上就是真实的子集和（没有取模）。

事实证明，在选择超递增序列 (b_1, \ldots, b_n) 时需要谨慎。例如，取自然选择 (b_i = 2^{i-1}) 会导致一些简单的攻击。我们不会详细讨论这个问题，因为事实是，无论使用什么样的超递增序列，Merkle-Hellman 方案（以及几乎所有后续变体）都可以被像 \(\mathrm{LLL}\) 这样的工具攻破。

背包密码的格攻击

1982 年，Shamir [Sha82] 展示了如何在多项式时间内攻破基本的 Merkle-Hellman 类加密方案。他的攻击使用了 Lenstra 提出的固定维度整数规划的多项式时间算法，该算法以 \(\mathrm{LLL}\) 为子程序。（Shamir 的攻击后来被推广，用于攻破许多 Merkle-Hellman 系统的变种。）紧接着，Lagarias 和 Odlyzko [LO83] 提出了一种不同类型的攻击，后来又被 Frieze [Fri86] 简化，该攻击能解出几乎所有“低密度”子集和问题的实例。

定义 3 密度

一个子集和问题的密度定义为 ( n / \max_i \log a_i )。

定理 4（Lagarias-Odlyzko，Frieze）

存在一个高效算法，对于从集合 ({1,\ldots,X}) 中独立均匀地选取的权重 (a_1,\ldots,a_n)，其中 (X \geq 2^{n2(1/2+\varepsilon)})，(\varepsilon > 0) 为任意常数，以及任意消息 (\mathbf{x} \in {0,1}^n)，若令 (s = \langle \mathbf{a}, \mathbf{x} \rangle)，则该算法以概率 (1 - 2^{-n2(\varepsilon - o(1))}) 输出 (\mathbf{x})。

注意上述子集和实例的密度大约是 (2/n)。

证明：
我们考虑一个子集和实例 ((\mathbf{a}=(a_1,\ldots,a_n), s=\langle \mathbf{a}, \mathbf{x} \rangle))，其中 (\mathbf{x} \in {0,1}^n)。不妨设 (s \geq (\sum_i a_i)/2)，否则可以将 (s) 替换为 ((\sum a_i) - s)，这相当于把 (\mathbf{x}) 所有位取反。注意此假设意味着 (\mathbf{x} \neq \mathbf{0})。

主要思想是构造一个格，使得 (\mathbf{x}) 是该格中最短的非零向量，且所有不平行于 (\mathbf{x}) 的格向量都长得多（至少大 (2^{n/2}) 倍）。由于 \(\mathrm{LLL}\) 能近似最短向量至一个 (2^{n/2}) 的因子，它将返回 (\mathbf{x})。

令 (B = \left\lceil \sqrt{n \cdot 2^n} \right\rceil)，定义以下格基：

[
\mathbf{B} =
\begin{pmatrix}
1 & & & \
& 1 & & \
& & \ddots & \
B a_1 & B a_2 & \ldots & -B s
\end{pmatrix}
\in \mathbb{Z}^{(n+1) \times (n+1)}
]

显然，(\binom{\mathbf{x}}{0} \in \mathcal{L} = \mathcal{L}(\mathbf{B}))。

我们会看到最后一行的 (B) 作用是放大不满足 (\langle \mathbf{a}, \mathbf{z} \rangle = z_{n+1} s) 的格向量的范数。

算法运行 \(\mathrm{LLL}\) 于基 (\mathbf{B}) 上，得到一个范数在最短向量 (\lambda_1(\mathcal{L})) 的 (2^{n/2}) 倍以内的非零格向量。接下来的分析表明，高概率下，所得向量是形如 (k \binom{\mathbf{x}}{0}) 的形式（(k) 为非零整数），从而得到 (\mathbf{x} \in {0,1}^n)。

注意，(\mathbf{B} \binom{\mathbf{x}}{1} = \binom{\mathbf{x}}{0} \in \mathcal{L}) 是非零格向量，其范数至多为 (\sqrt{n})。而任何格向量的最后一坐标都是 (B) 的倍数，若该坐标非零，则该向量长度至少为
[
B > 2^{n/2} \cdot |\mathbf{x}| \geq 2^{n/2} \cdot \lambda_1(\mathcal{L})
]
因此，\(\mathrm{LLL}\) 总是返回一个最后一坐标为零、长度不超过 (2^{n/2} \sqrt{n}) 的非零格向量。我们接着证明，高概率下，唯一满足这些条件的非零格向量是 (\binom{\mathbf{x}}{0}) 的整数倍。

取任意 (\binom{\mathbf{z}}{0} \in \mathbb{Z}^{n+1})，其中 (|\mathbf{z}| \leq 2^{n/2} \sqrt{n})，且 (\mathbf{z}) 不是 (\mathbf{x}) 的整数倍。我们要估计该向量属于格 (\mathcal{L}) 的概率，也即存在 (z_{n+1} \in \mathbb{Z}) 使得 (\binom{\mathbf{z}}{0} = \mathbf{B} \binom{\mathbf{z}}{z_{n+1}}) 的概率。

这等价于：

[
s \cdot |z_{n+1}| = |\langle \mathbf{a}, \mathbf{z} \rangle| \leq |\mathbf{z}| \sum a_i \leq 2 |\mathbf{z}| s,
]

从而得 (|z_{n+1}| \leq 2 |\mathbf{z}|)。固定这样的 (z_{n+1})，则有：

[
\langle \mathbf{a}, \mathbf{z} \rangle = z_{n+1} \cdot s = z_{n+1} \langle \mathbf{a}, \mathbf{x} \rangle,
]

这推出 (\langle \mathbf{a}, \mathbf{y} \rangle = 0)，其中 (\mathbf{y} = \mathbf{z} - z_{n+1} \mathbf{x})。由于 (\mathbf{z}) 不是 (\mathbf{x}) 的整数倍，存在某个 (y_i \neq 0)，不妨设 (i = 1)，则

[
a_1 = -\left( \sum_{i=2}^n a_i y_i \right) / y_1.
]

据此，对于固定的满足上述条件的 (\mathbf{z}, z_{n+1})，有：

[
\Pr_{\mathbf{a}}[\langle \mathbf{a}, \mathbf{y} \rangle = 0] = \Pr_{a_1}\left[ a_1 = -\left( \sum_{i=2}^n a_i y_i \right) / y_1 \right] \leq 1/X,
]

定义右侧的值为： \(c=-\frac{\sum_{i=2}^n a_i y_i}{y_1}\)
情况 \(1\)：\(c \notin \mathbb{Z}\) 此时方程无解，概率为 \(0\) ;
情况 \(2\)：\(c \in \mathbb{Z}\) 若 \(c \notin\{1,2, \ldots, X\}\) ，则 \(a_1\) 无法取到该值，概率为 \(0\) 。若 \(c \in\{1,2, \ldots, X\}\) ，则 \(a_1=c\) 的概率为 \(1 / X\) ，因为 \(a_1\) 是均匀随机的。

为什么可以固定其他变量？
理解 \(1\)：由于 \(a_1\) 独立于 \(a_2, \ldots, a_n\) ，在固定其他变量后，\(a_1\) 的条件分布仍为均匀分布 \(\mathcal{U}\{1, \ldots, X\}\) 。
理解 \(2\)：利用全概率公式，将总概率分解为对所有可能的 \(c_2, \ldots, c_n\) 取值的加权平均：\(\operatorname{Pr}[\langle\mathbf{a}, \mathbf{y}\rangle=0]=\sum \operatorname{Pr}\left[a_2=c_2, \ldots, a_n=c_n\right] \cdot \operatorname{Pr}\left[\left.a_1=-\frac{\sum_{i=2}^n c_i y_i}{y_1} |\, a_2=c_2, \ldots, a_n=c_n\right]\right.\) 而 \(\operatorname{Pr}\left[a_1=-\frac{\sum_{i=2}^n c_i y_i}{y_1} |\, a_2=c_2, \ldots, a_n=c_n\right]= \begin{cases}1 / X, & \text { 若右侧值在 }\{1, \ldots, X\} \text { 内, } \\ 0, & \text { 否则. }\end{cases}\)

最后我们利用得到的界考虑所有可能的 (\mathbf{z}, z_{n+1}) 的数目。由于 (|\mathbf{z}| \leq 2^{n/2} \sqrt{n} \leq B)，每个 (\mathbf{z}) 分量绝对值不超过 (B)，且 (|z_{n+1}| \leq 2B)，因此所有可能的组合个数至多为：

[
(2B + 1)^n \cdot (4B + 1) \leq (5B)^{n+1} \leq 2^{n2(1/2 + o(1))}.
]

由于 (X = 2^{n2(1/2 + \varepsilon)})，最终得到某个满足条件的 (\binom{\mathbf{z}}{0} \in \mathcal{L}) 存在的概率至多为：

[
2^{-n2(\varepsilon - o(1))},
]

\(\square\)

首先，估计满足条件的非目标向量的组合个数最多为 \(2^{n^2(1 / 2+o(1))}\) ，而每个组合对应的失败概率为 \(1 / X=2^{-n^2(1 / 2+\epsilon)}\) 。总失败概率上界为二者乘积，即 \(2^{-n^2(\epsilon-o(1))}\) ，故成功概率为 \(1-2^{-n^2(\epsilon-o(1))}\) 。

附录 1 公钥密码的典型流程

以发送加密消息为例：
\(1\). 接收方生成密钥对：生成公钥（公开）和私钥（保密）。
\(2\). 发送方获取公钥：通过公开渠道（如网站、证书）获取接收方的公钥。
\(3\). 加密与发送：发送方用公钥加密消息，密文发送给接收方。
\(4\). 解密：接收方用私钥解密，无需传递私钥。

附录 2 子集和问题的困难性

子集和问题表面上看似可以通过穷举所有子集来求解，但之所以被认为是“困难”的，核心原因在于穷举的代价会随着输入规模指数级增长，导致它在实际应用中不可行。
子集和问题的穷举解法需要检查所有可能的子集。对于一个包含 ( n ) 个元素的集合，其子集数量为 ( 2^n )，因此穷举的时间复杂度为 ( O(2^n) )。
当 ( n ) 增大时，子集数量会迅速超过任何实际计算能力：
( n = 20 ): ( 2^{20} \approx 100 ) 万（普通计算机可在秒级完成）；
( n = 30 ): ( 2^{30} \approx 10 ) 亿（需要分钟到小时级时间）；
( n = 60 ): ( 2^{60} \approx 10^{18} )（即使用超级计算机也需数百年）；
( n = 100 ): ( 2^{100} \approx 1.27 \times 10^{30} )（远超宇宙年龄）。
子集和的困难性不是由于问题本身复杂，而是因为它代表了 \(\mathrm{NP}\) 完全问题的共性——指数级搜索空间。