3.1.2 Xing 的改进

对于有限域 \(\boldsymbol{F}_q\) 上的线性编码 $ C $，我们用 \(n(C)\) 、 \(k(C)\) 和 \(d(C)\) 分别表示 \(C\) 的长度、维数和最小距离。令 $U_q^{\text{lin}} $ 表示所有有序对 \((\delta, R) \in \boldsymbol{R}^2\) 的集合，使得存在一列无限长的线性编码 $ C_1, C_2, \dots $ ，其定义在 \(\boldsymbol{F}_q\) 上，并满足 $ n(C_i) \to \infty $ 且

\[\delta=\lim _{i \rightarrow \infty} \frac{d\left(C_i\right)}{n\left(C_i\right)}, \quad R=\lim _{i \rightarrow \infty} \frac{k\left(C_i\right)}{n\left(C_i\right)} \]

关于 $ U_q^{\text{lin}} $ 有如下命题：

引理 1

存在一个连续函数 \(\alpha_q^{\text{lin}}(\delta)\)，其中 \(\delta \in [0,1]\)，使得

\[U_q^{\text{lin}}=\left\{(\delta, R) \in \boldsymbol{R}^2 \mid 0 \leq R \leq \alpha_q^{\operatorname{lin}}(\delta), 0 \leq \delta \leq 1\right\} \]

此外，\(\alpha_q^{\operatorname{lin}}(0)=1\)，对于 \(\delta \in [(q-1)/q, 1]\) 有 \(\alpha_q^{\operatorname{lin}}(\delta)=0\)，并且 \(\alpha_q^{\text{lin}}(\delta)\) 在区间 \([0, (q-1)/q]\) 上是单调递减的。

我们需要定义一些关于有限域上代数曲线有理点数量的记号。

当我们讨论有限域 \(\boldsymbol{F}_q\) 上的代数曲线时，我们始终指的是在 \(\boldsymbol{F}_q\) 上定义的光滑、射影的、绝对不可约的代数曲线。若 \(\mathcal{X}\) 是这样的一条曲线，简记为 \(\mathcal{X} / \boldsymbol{F}_q\)，则用 $ g(\mathcal{X}) $ 表示 \(\mathcal{X}\) 的亏格。若 \(\mathcal{X}\) 上的一点具有齐次坐标，并且所有坐标都属于 \(\boldsymbol{F}_q\)，则称该点是 \(\boldsymbol{F}_q\)-有理的。记 $ N\left(\mathcal{X} / \boldsymbol{F}_q\right) $ 为 \(\mathcal{X} / \boldsymbol{F}_q\) 的 \(\boldsymbol{F}_q\)-有理点的数量。曲线 \(\mathcal{X}\) 的亏格记作 $ g(\mathcal{X}) $。根据 Weil 界（曲线上有理点数目的一个上界），以下两个定义是合理的。

对任意素数幂 $ q $ 及任意整数 $ g \geq 0 $，定义

\[N_q(g)=\max N\left(\mathcal{X} / \boldsymbol{F}_q\right) \]

其中最大值取遍所有满足 $ g(\mathcal{X})=g $ 的曲线 \(\mathcal{X} / \boldsymbol{F}_q\)。
我们还定义如下的渐近量：

\[A(q):=\limsup _{g \rightarrow \infty} \frac{N_q(g)}{g} \]

平均每亏格所能增加的有理点数量

对任意素数幂 $ q $,Goppa 的构造给出了一个超越渐进G—V界的新的码率下界

\[R_G(q, \delta)=1-\frac{1}{A(q)}-\delta\tag{1} \]

Tsfasman等人关心 \(A(q)\) 的渐进上界的改进并由此给出了以下码率下界

\[R_{\mathrm{TVZ}}(q, \delta)=1-\frac{1}{\sqrt{q}-1}-\delta\tag{2} \]

我们的问题是，是否可以改变 Goppa 的构造使得直接对不等式 \((1)\) 进行改进。目前没有理由认为 \((1)\) 是 Goppa 几何编码所能给出的最优界，因为 \((1)\) 是一条直线。可以想象，在 \(\delta=(q-1) /(2 q-1)\) 附近改进 \((1)\) 可能较为困难。然而，对于那些远离 \((q-1) /(2 q-1)\) 的 \(\delta\)，改进 \((1)\) 应该是可能的。

为了构造 Goppa 几何编码，我们需要选择 $ n $ 个有理点以及一个除子 $ G $（通常为了简化问题都是考虑由有理点构成的“有理除子”——更严格的说，有理除子也可以不单单由有理点构成）。Goppa 对其几何编码参数的估计对任意有理除子 $ G $ 都成立。我们的想法是选择一个特定的有理除子 $ G $，以改进 Goppa 对参数的估计。

首先，让我们回顾 Goppa 对代数几何编码的构造。

引理 2 Goppa的构造(代数几何编码)

设 $ \mathcal{X} / \boldsymbol{F}_q $ 为亏格 $ g $ 的代数曲线，且 $ P_1, P_2, \dots, P_n $ 为 $ \mathcal{X} $ 上 $ n $ 个不同的有理点。选取一个除子 $ G $ 使得 $ g \leq \operatorname{deg}(G) < n $ 且满足

\[\operatorname{Supp}(G) \cap \{P_1, P_2, \dots, P_n\} = \emptyset \]

则 $ C(P_1, P_2, \dots, P_n ; G) $ 是定义在 $ \boldsymbol{F}_q $ 上的一个 $ [n, k, d] $ 线性编码，其参数满足

\[k \geq \operatorname{deg}(G) - g + 1, \quad d \geq n - \operatorname{deg}(G) \]

此外，当 $ \operatorname{deg}(G) \geq 2g - 1 $ 时，编码的维数取等号，即 $ k = \operatorname{deg}(G) - g + 1 $。

上述命题对任意有理除子 $ G $ 给出了编码 $ C(P_1, P_2, \dots, P_n ; G) $ 的参数估计。可以想见，若选择特定的除子 $ G $，这些参数可能会得到改进。

命题 3

设 $ \mathcal{X} / \boldsymbol{F}_q $ 为亏格 $ g $ 的代数曲线，并且至少包含一个有理点 $ P $。设 $ s \geq g $ 为一个正整数，令 $ S $ 为一些次数为 $ s $ 的除子构成的集合。若 $ |S| $ 小于除子类数 $ h(\mathcal{X}) $，则存在一个次数为 $ s $ 的正除子 $ H $，使得 $ H $ 不与 $ S $ 中的任何除子等价。

证明：对于任意次数为 \(0\) 的除子 $ D $，由黎曼-罗赫定理可得

\[\ell(D+sP) \geq s - g + 1 \geq 1 \]

取 $ \mathcal{L}(D+sP) $ 中的一个非零函数 $ f $，定义

\[G := \operatorname{div}(f) + D + sP \]

则 $ G $ 是一个次数为 $ s $ 的正除子，并且 $ G - sP $ 与 $ D $ 等价。这意味着存在 $ h := h(\mathcal{X}) $ 个次数为 $ s $ 的正除子 $ H_1, H_2, \dots, H_h $，使得 $ H_1 - sP, H_2 - sP, \dots, H_h - sP $ 彼此不等价。由于 $ |S| < h $，可以找到 $ 1 \leq j \leq h $，使得对 $ S $ 中的任意除子 $ R \(，\) R - sP $ 不属于除子类 $ \overline{H_j - sP} $，即 $ R $ 不与 $ H_j $ 等价。因此，取 $ H := H_j $ 即得所求结论。

\(D(K)\) 表示函数域 \(K\) 上所有除子构成的群，对于 \(\alpha \in K^*,div(\alpha)\) 叫作 \(K\) 的主除子，由于 \(div(\alpha)+div(\beta)=div(\alpha\beta),-div(\alpha)=div(\alpha^{-1})\),所以 \(K\) 的全部主除子形成 \(D(K)\) 的一个加法子群，叫作 \(K\) 的主除子群，表示成 \(P(K)\)。除子类群 \(:=C(K)=\frac{D(K)}{P(K)}\),零次除子类群 \(:=C^0(K)=\frac{D^0(K)}{P(K)}\)．对于每个除子 \(A \in D(K), C(K)\) 中的元素 \(A+P(K)\) 叫作一个除子类，表示成 \([A]\) ．当 \(\operatorname{deg} A=0\) 时，\([A]\) 是 \(C^0(K)\)中的元素，叫作零次除子类．同一除子类中的除子 \(A\) 和 \(B\) 叫作彼此等价的，表示成 \(A \sim B\) ，即彼此相差一个主除子：\(A-B=\operatorname{div}(\alpha)\left(\alpha \in K^*\right)\) ．特别地，彼此等价的除子有相同的次数．我们有

\[\frac{C(K)}{C^0(K)} \cong \frac{D(K)}{D^0(K)} \]

对于一般的函数域 \(K\) ，每个零次除子不必为主除子，即 \(P(K)\) 可能是 \(D^0(K)\) 的真子群．事实上可以证明：对于每个函数域 \(K, C^0(K)=\frac{D^0(K)}{P(K)}\) 都是有限（交换）群．群 \(C^0(K)\) 的阶 \(h(k)=\left|C^0(K)\right|\) 叫作函数域 \(K\)的（零次）除子类数．于是：\(P(K)=D^0(K)\) 当且仅当 \(h(K)=1\)．在此基础上很容易证明对于每个 \(n \in \mathbb{Z}\) ， \(D(K)\) 中的所有 \(n\) 次除子也分成 \(h(K)\) 个除子类，从而命题 \(3\) 是显然的．

而且由此可知命题 \(3\) 并不需要 \(s\geq g\) 的条件，但是由于 Goppa 的构造要求 \(s\geq g\) 这个条件所以带上这个条件处理问题也是没问题的。

对于 $ n $ 个不同的有理点 $ P_1, P_2, \dots, P_n $ 以及两个满足 $ s \geq m $ 的非负整数，定义 $ N_{s, m} := N_{s, m}(P_1, P_2, \dots, P_n) $ 为集合

\[S_{s, m}(P_1, P_2, \dots, P_n) \]

的基数，其中

\[S_{s, m}(P_1, P_2, \dots, P_n) := \left\{ \sum_{P \in I} P + D \mid I \subseteq \{P_1, P_2, \dots, P_n\}, |I| = m, D \text{ 是次数为 } s - m \text{ 的正有理除子} \right\} \]

显然，$ S_{s, m}(P_1, P_2, \dots, P_n) $ 是一些次数为 $ s $ 的正除子构成的集合。

定理 4 Xing 的构造

设 \(\mathcal{X} / \boldsymbol{F}_q\) 为亏格 \(g\) 的代数曲线，且设 \(P_1, P_2, \ldots, P_n\) 为 \(\mathcal{X}\) 上 \(n\) 个不同的有理点。设 \(s, m\) 为满足 \(m \leq \min \{s, n\}\) 且 \(s \geq g\) 的非负整数。若 \(N_{s, m}\) 小于除子类数 \(h(\mathcal{X})\)，则存在次数为 \(s\) 的除子 \(G\)，使得 \(\operatorname{Supp}(G) \cap\left\{P_1, P_2, \ldots, P_n\right\}=\emptyset\)，并且 \(C\left(P_1, P_2, \ldots, P_n ; G\right)\) 是 \(\boldsymbol{F}_q\) 上的 \([n, k, d]\) 线性编码，满足

\[k \geq \operatorname{deg}(G)-g+1=s-g+1, \quad d \geq n-m+1 \]

此外，若 \(\operatorname{deg}(G) \geq 2g-1\)，则编码的维数 \(k\) 等于 \(\operatorname{deg}(G)-g+1\)。

注意到 \(d\geq n-m+1>n-s\),所以如此选取给出的参数估计严格好于 Goppa 的构造

证明：由于 \(N_{s, m}<h(\mathcal{X})\)，根据引理 \(3\)，存在次数为 \(s\) 的正除子 \(H\)，使得 \(H\) 不与 \(S_{s, m}\left(P_1, P_2, \ldots, P_n\right)\) 中的任意除子等价。

我们声称

\[\mathcal{L}\left(H-\sum_{P \in I} P\right)=\{0\} \]

对任意满足 \(|I|=m\) 的子集 \(I \subset\left\{P_1, P_2, \ldots, P_n\right\}\) 都成立。

假设不成立，即存在 \(I_0 \subset\left\{P_1, P_2, \ldots, P_n\right\}\) 使得 \(\mathcal{L}\left(H-\sum_{P \in I_0} P\right) \neq\{0\}\)。取 \(x\) 为 \(\mathcal{L}\left(H-\sum_{P \in I_0} P\right)\) 中的非零函数，则

\[\operatorname{div}(x)+H-\sum_{P \in I_0} P \geq 0 \]

令

\[D=\operatorname{div}(x)+H-\sum_{P \in I_0} P \]

则 \(H\) 等价于正除子 \(D+\sum_{P \in I_0} P\)，而该除子属于 \(S_{s, m}\left(P_1, P_2, \ldots, P_n\right)\)，这与 \(H\) 的选择矛盾。

对于每个 \(i\)，根据强逼近定理，存在函数 \(t_i\) 使得

\[\nu_{P_j}\left(t_i\right)= \begin{cases}0, & \text { if } j \neq i \\ 1, & \text { if } j=i\end{cases} \]

定义除子

\[G:=H+\operatorname{div}\left(\prod_{i=1}^n t_i^{-\nu_{P_i}(H)}\right) \]

则 \(\operatorname{Supp}(G) \cap\left\{P_1, P_2, \ldots, P_n\right\}=\emptyset\) 且 \(G\) 与 \(H\) 等价。因此，

\[\mathcal{L}\left(G-\sum_{P \in I} P\right)=\{0\} \]

对任意满足 \(|I|=m\) 的子集 \(I\) 都成立。设 \(f\) 是 \(\mathcal{L}(G)\) 的非零元素，在 \(P_1, P_2, \ldots, P_n\) 之间恰有 \(r\) 个零点，则 \(f \in \mathcal{L}\left(G-\sum_{P \in J} P\right)\)，其中 \(J \subset\left\{P_1, P_2, \ldots, P_n\right\}\) 且 \(|J|=r\)。因此 \(r< m\)，从而码字 \(\left(f\left(P_1\right), f\left(P_2\right), \ldots, f\left(P_n\right)\right)\) 的权重至少为 \(n-r \geq n-m+1\)。这也表明映射

\[\phi: \mathcal{L}(G) \longrightarrow \boldsymbol{F}_q^n, \quad f \mapsto\left(f\left(P_1\right), f\left(P_2\right), \ldots, f\left(P_n\right)\right) \]

是单射，因为 \(m<n\)。因此，编码 \(C\left(P_1, P_2, \ldots, P_n ; G\right)\) 的维数等于 \(\ell(G)\)，由黎曼–罗赫定理可得其至少为 \(\operatorname{deg}(G)-g+1\)。\(\square\)

示例 5

考虑定义为

\[y^2+y=\frac{x(x+1)}{x^3+x+1} \]

的亏格为 \(2\) 的代数曲线 \(\mathcal{X} / \boldsymbol{F}_2\)，该曲线具有 \(6\) 个有理点，且其除子类数 \(h(\mathcal{X})=19\)。设 \(P_1, P_2, \ldots, P_6\) 为其全部有理点。取 \(s=m=4\)。由于 \(N_{4,4}=\binom{6}{4}=15<h(\mathcal{X})\)，根据定理 \(4\)，存在次数为 \(4\) 的除子 \(G\)，使得编码 \(C\left(P_1, P_2, \ldots, P_6 ; G\right)\) 具有参数

\[[6, s-g(\mathcal{X})+1, d \geq 6-m+1]=[6,3, d \geq 3] \]

即 \(C\left(P_1, P_2, \ldots, P_6 ; G\right)\) 是一个二元 \([6,3,3]\) 线性编码。

然而，若应用引理 \(2\)，我们只能得到 \(C\left(P_1, P_2, \ldots, P_6 ; G\right)\) 是一个二元 \([6,3, d \geq 2]\) 线性编码。

这条曲线的亏格，由 Riemman-Hurwitz 公式计算得到。

显然，为了从定理 \(4\) 中获得较好的编码，我们需要对 \(N_{s, m}\left(P_1, P_2, \ldots, P_n\right)\) 进行合理估计。以下结果可直接从 \(N_{s, m}\left(P_1, P_2, \ldots, P_n\right)\) 的定义推出。

命题 6 \(N_{s,m}\) 的简单估计

设 \(\mathcal{X} / \boldsymbol{F}_q\) 为亏格 \(g\) 的代数曲线。对所有 \(i \geq 0\)，设 \(A_i\) 表示次数为 \(i\) 的正有理除子的个数。则对于任意有理点 \(P_1, P_2, \ldots, P_n\) 及满足 \(m \leq \min \{s, n\}\) 的 \(m\)，有

\[N_{s, m}\left(P_1, P_2, \ldots, P_n\right) \leq\binom{ n}{m} \times A_{s-m} \]

结合定理 \(4\) 和命题 \(6\)，可以得到以下结果。

推论 7

设 \(\mathcal{X} / \boldsymbol{F}_q\) 为亏格 \(g\) 且至少有 \(n\) 个有理点的代数曲线。设 \(h(\mathcal{X})\) 为 \(\mathcal{X}\) 的除子类数。对所有 \(i \geq 0\)，设 \(A_i\) 表示次数为 \(i\) 的正有理除子的个数。若存在两个非负整数 \(s, m\) 满足 \(m \leq \min \{s, n\}\) 及 \(s \geq g\)，且

\[\binom{n}{m} \times A_{s-m}<h(\mathcal{X}) \]

则存在一个定义在 \(\boldsymbol{F}_q\) 上的 \([n, k, d]\) 线性编码，满足

\[k \geq s-g+1, \quad d \geq n-m+1 \]

此外，若 \(s \geq 2 g-1\)，则编码的维数 \(k\) 等于 \(s-g+1\)。

接下来，我们面临估计 \(A_i\) 和 \(h(\mathcal{X})\) 的问题。

设 \(\mathcal{X} / \boldsymbol{F}_q\) 为亏格 \(g\) 的代数曲线。定义 \(A_i(\mathcal{X})\)（若无歧义，可简记为 \(A_i\)）为次数 \(i \geq 0\) 的所有正 \(\boldsymbol{F}_q\)-有理除子的个数。显然，\(A_0=1\)，且 \(A_1\) 为 \(\mathcal{X}\) 上的有理点数目。

\(\mathcal{X} / \boldsymbol{F}_q\) 的ζ 函数定义为幂级数

\[Z(T):=\sum_{i=0}^{\infty} A_i T^i \]

ζ 函数可以写成有理函数的形式

\[Z(T)=\frac{L(T)}{(1-T)(1-q T)} \]

其中，\(L(T)\) 是一个次数为 \(2g\) 的整系数多项式。所有 \(T^{2g} L(1 / T)\) 的根的绝对值均为 \(\sqrt{q}\)。\(L(T)\) 被称为 \(\mathcal{X} / \boldsymbol{F}_q\) 的L-多项式。

命题 8

设 \(\mathcal{X} / \boldsymbol{F}_q\) 为亏格 \(g\) 的代数曲线。设 \(A_n\) 为次数为 \(n\) 的所有正 \(\boldsymbol{F}_q\)-有理除子的个数。则对于任意 \(2 \leq t \leq 2g\)，有

\[A_t=\sum_{i=2}^t \frac{q^{t+1-i}-1}{q-1} a_i+\frac{q^t-1}{q-1} A_1-\frac{q^t-q}{q-1} \]

其中，\(a_i\) 为 \(L\)-多项式的系数，即 \(L(T)=\sum_{i=0}^{2g} a_i T^i\)。

证明：所需结论直接由等式

\[\sum_{i=0}^{\infty} A_i T^i=Z(T)=\frac{L(T)}{(1-T)(1-q T)} \]

推出。\(\square\)

不清楚细节可参见结尾附录

推论 9

设 \(\mathcal{X} / \boldsymbol{F}_q\) 为亏格 \(g\) 的代数曲线。设 \(A_n\) 为次数为 \(n\) 的所有正 \(\boldsymbol{F}_q\)-有理除子的个数。则对于任意 \(2 \leq t \leq 2 g\)，有

\[A_t \leq \frac{q^{t+1}}{q-1} \sum_{i=2}^t\binom{2 g}{i} q^{-i / 2}+\frac{q^t-1}{q-1} N(\mathcal{X}) \]

证明：设 \(a_i\) 为 \(L\)-多项式 \(L(T)=\sum_{j=0}^{2g} a_j T^j\) 中的 \(T^i\) 的系数，则由于 \(T^{2 g} L(1 / T)\) 的所有根的绝对值均为 \(q^{1/2}\)，因此

\[\left|a_i\right| \leq\binom{2 g}{i} q^{i / 2} \]

不清楚细节可参加结尾附录
由命题 \(8\)，可得

\[\begin{aligned} A_t & =\left|\sum_{i=2}^t \frac{q^{t+1-i}-1}{q-1} a_i+\frac{q^t-1}{q-1} A_1-\frac{q^t-q}{q-1}\right| \\ & \leq \sum_{i=2}^t \frac{q^{t+1-i}-1}{q-1}\left|a_i\right|+\left|\frac{q^t-1}{q-1} A_1-\frac{q^t-q}{q-1}\right| \\ & \leq \sum_{i=2}^t \frac{q^{t+1-i}-1}{q-1}\binom{2 g}{i} q^{i / 2}+\frac{q^t-1}{q-1} A_1 \\ & \leq \frac{q^{t+1}}{q-1} \sum_{i=2}^t\binom{2 g}{i} q^{-i / 2}+\frac{q^t-1}{q-1} N(\mathcal{X}) \end{aligned} \]

为了进一步估计 $ A_t $，我们需要以下结果，该结果可直接从斯特林公式推导得出。

引理 10

\((1)\) 设 $ r>1 $ 为实数，$ n $ 为正整数。设 $ \sigma $ 为满足 $ 0<\sigma \leq 1-1 / r $ 的正实数，并且 $ \sigma n $ 为整数。则有

\[\sum_{i=0}^{\sigma n}\binom{n}{i}(r-1)^i \leq r^{n H_r(\sigma)} \]

\((2)\) 设 $ n $ 为正整数，且 $ 0 \leq \delta \leq 1 $ 为满足 $ \delta n $ 为整数的实数，则

\[\binom{n}{\delta n} \leq 2^{n H_2(\delta)} \]

这是一个对称的估计

推论 11

设 $ \sigma $ 满足 $ 0<\sigma<2 /(\sqrt{q}+1) $。设 $ \mathcal{X}_i / \boldsymbol{F}_q $ 为亏格趋于无穷的一族曲线，则有

\[\limsup _{g\left(\mathcal{X}_i\right) \rightarrow \infty} \frac{\log _q\left(A_{\left\lfloor\sigma g\left(\mathcal{X}_i\right)\right\rfloor}\left(\mathcal{X}_i\right)\right)}{g\left(\mathcal{X}_i\right)} \leq \frac{\sigma}{2}+2\left(\log _q 2\right) H_2\left(\frac{\sigma}{2}\right) \]

其中，$ A_{\left\lfloor\sigma g\left(\mathcal{X}_i\right)\right\rfloor}\left(\mathcal{X}_i\right) $ 表示 \(\mathcal{X}_i / \boldsymbol{F}_q\) 上次数为 $ \left\lfloor\sigma g\left(\mathcal{X}_i\right)\right\rfloor $ 的所有正有理除子的个数。

之所以估计这个式子，是因为我们有引理 \(12\)。

证明：令 $ l=1+1 / \sqrt{q}$ 。 设 \(g_i=g\left(\mathcal{X}_i\right)\) ，$ t_i=\left\lfloor\sigma g\left(\mathcal{X}_i\right)\right\rfloor$ 。则对于所有 \(i \geq 1\)，有

\[\sigma_i:=\frac{t_i}{2 g_i} \leq \frac{\sigma}{2} \leq 1-\frac{1}{l} \]

且当 $ i \to \infty $ 时，$ \sigma_i \to \sigma / 2 $。由推论 3.2 可得

\[\begin{aligned} A_{\left\lfloor\sigma g\left(\mathcal{X}_i\right)\right\rfloor}\left(\mathcal{X}_i\right) &=A_{t_i}\left(\mathcal{X}_i\right) \\ & \leq \frac{q^{t_i+1}}{q-1} \sum_{j=2}^{t_i}\binom{2 g_i}{j} q^{-j / 2}+\frac{q^{t_i}-1}{q-1} N\left(\mathcal{X}_i\right) \\ & \leq q^{t_i+1} N\left(\mathcal{X}_i\right) \sum_{j=0}^{t_i}\binom{2 g_i}{j} q^{-j / 2} \\ & \leq q^{t_i+1} N\left(\mathcal{X}_i\right) l^{2 g_i H_l\left(\sigma_i\right)} . \end{aligned} \]

此处放缩注意指标的改变即可

因此，

\[\begin{aligned} & \frac{\log _q\left(A_{\left\lfloor\sigma g\left(\mathcal{X}_i\right)\right\rfloor}\left(\mathcal{X}_i\right)\right)}{g\left(\mathcal{X}_i\right)} \\ & \quad \leq \frac{t_i+1}{g_i}+\frac{\log _q\left(N\left(\mathcal{X}_i\right)\right)}{g_i}+\frac{\left(\log _q l\right) \cdot 2 g_i H_l\left(\sigma_i\right)}{g_i} \\ & \quad \longrightarrow \sigma+2\left(\log _q l\right) H_l\left(\frac{\sigma}{2}\right)=\frac{\sigma}{2}+2\left(\log _q 2\right) H_2\left(\frac{\sigma}{2}\right). \end{aligned} \]

引理 12

设 $ \mathcal{X}_i / \boldsymbol{F}_q $ 为一族亏格趋于无穷的曲线，且满足

\[\lim _{g\left(\mathcal{X}_i\right) \rightarrow \infty} \frac{N\left(\mathcal{X}_i\right)}{g\left(\mathcal{X}_i\right)} \geq A>0 \]

则有

\[\liminf _{g\left(\mathcal{X}_i\right) \rightarrow \infty} \frac{\log _q\left(h\left(\mathcal{X}_i\right)\right)}{g\left(\mathcal{X}_i\right)} \geq 1+A \cdot \log _q\left(\frac{q}{q-1}\right). \]

\(\square\)

---

我们定义一个函数

\[f_q(x) = \frac{x}{2} + 2\left( \log_q 2 \right) H_2\left(\frac{x}{2}\right) \]

显然，\(f_q(x)\)在区间\((0, 1)\)上是连续且严格递增的。因此，反函数\(f_q^{-1}\)存在。此外，对于任意实数\(u \in \left[0, 1 / 2 + 2 \log_q 2\right]\)，方程 \(f_q(x) = u\) 存在唯一解。

此处唯一解应当指的是 \((0,1)\) 范围内的唯一解，可以发现 \(f_q(x)\) 在 \((0,2)\) 先增后减。

定义函数 \(h_q(y)\) 如下：

\[h_q(y) = \begin{cases} f_q^{-1}(y), & \text{如果 } 0 < y < \frac{2}{\sqrt{q} + 1} (<\frac{1}{2}+2log_q 2\\ 0, & \text{否则} \end{cases} \]

显然在区间 \((0, \frac{2}{\sqrt{q} + 1})\) 内 \(h_q(y)\) 单调增值域为 \((0,h_q(\frac{2}{\sqrt{q} + 1}))<1\)

显然，\(h_q(y)\)是一个定义良好的函数，其定义域为\((-\infty, +\infty)\)。\(h_q(x)\)在区间\((0, \frac{2}{\sqrt{q} + 1})\)内也是连续的。

我们定义函数

\[\begin{aligned} R(q, \delta) := & \ 1 - \delta - \frac{1}{A} \\ & + \frac{1}{A} h_q\left(1 + A \cdot \log_q\left(\frac{q}{q-1}\right) - A \left(\log_q 2 \right) H_2(\delta)\right) \end{aligned} \]

定理 13

如果 \(A \leq A(q)\)是一个正数，那么对于任意\(0 < \delta < 1\)，

\[\alpha_q(\delta) \geq R(q, \delta) \]

证明：首先我们固定\(\delta \in (0, 1)\)。如果

\[1 + A \log_q\left( \frac{q}{q-1} - A \left( \log_q 2 \right) H_2(\delta) \right) \]

不在区间\((0, \frac{2}{\sqrt{q} + 1})\)内，那么我们的界限就是Ts-fasman-Vlăduţ-Zink界限。

现在假设 \(1 + A \cdot \log_q \left( \frac{q}{q-1} - A \left( \log_q 2 \right) H_2(\delta) \right)\)位于区间\((0, \frac{2}{\sqrt{q} + 1})\)内。令\(\epsilon\)为任意小的正数，使得\(1 + A \cdot \log_q \left( \frac{q}{q-1} - A \left( \log_q 2 \right) H_2(\delta) - \epsilon \right)\)仍然位于\((0, \frac{2}{\sqrt{q} + 1}) \subseteq \left( 0, 1/2 + 2 \log_q 2 \right)\)内。令\(\sigma\)为方程

\[f_q(x) = 1 + A \log_q\left( \frac{q}{q-1} - A \left( \log_q 2 \right) H_2(\delta) - \epsilon \right) \]

的唯一解，即

\[\begin{aligned} \sigma & = f_q^{-1}\left( 1 + A \cdot \log_q\left( \frac{q}{q-1} \right) - A \left( \log_q 2 \right) H_2(\delta) - \epsilon \right) \\ & = h_q\left( 1 + A \cdot \log_q\left( \frac{q}{q-1} \right) - A \left( \log_q 2 \right) H_2(\delta) - \epsilon \right) \end{aligned} \]

选择一族曲线\(\mathcal{X}_i / \boldsymbol{F}_q\)，使得其亏格逐渐增加，并满足

\[\lim_{i \to \infty} \frac{N(\mathcal{X}_i)}{g(\mathcal{X}_i)} = A(q) \]

令\(n_i \leq N(\mathcal{X}_i)\)，使得\(\lim_{i \to \infty} \frac{n_i}{g(\mathcal{X}_i)} = A\)。定义\(m_i = \left\lfloor (1 - \delta) n_i \right\rfloor\)，并令\(s_i = m_i + \left\lfloor \sigma g(\mathcal{X}_i) \right\rfloor\)，对于所有\(i \geq 1\)。然后，\(m_i / n_i \to 1 - \delta\)，且\(\left( s_i - m_i \right) / g(\mathcal{X}_i) \to \sigma\)。

\(n_i\) 的选取可以做到，并且如上的选取方式满足 \(m_i\leq s_i,m_i\leq n_i\)

根据引理 \(10\) 和推论 \(11\)，我们有

\[\begin{aligned} & \lim_{i \to \infty} \sup \frac{\log_q\left( \binom{n_i}{m_i} \times A_{s_i - m_i}(\mathcal{X}_i) \right)}{g(\mathcal{X}_i)} \\ & \leq \lim_{i \to \infty} \frac{n_i \left( \log_q 2 \right) H_2(\delta)}{g(\mathcal{X}_i)} + \frac{\sigma}{2} + 2\left( \log_q 2 \right) H_2\left( \frac{\sigma}{2} \right) \\ & = A \cdot \left( \log_q 2 \right) \cdot H_2(\delta) + \frac{\sigma}{2} + 2\left( \log_q 2 \right) H_2\left( \frac{\sigma}{2} \right) \end{aligned} \]

根据引理 \(12\)，我们有

\[\liminf_{i \to \infty} \frac{\log_q\left( h(\mathcal{X}_i) \right)}{g(\mathcal{X}_i)} \geq 1 + A \cdot \log_q \left( \frac{q}{q-1} \right) \]

由于

\[f_q(\sigma) = 1 + A \log_q\left( \frac{q}{q-1} - A \left( \log_q 2 \right) H_2(\delta) - \epsilon \right) \]

即

\[\begin{aligned} 1 + A \cdot \left( \log_q 2 \right) \cdot \log_q \left( \frac{q}{q-1} \right) = A \cdot H_2(\delta) + \frac{\sigma}{2} + 2\left( \log_q 2 \right) H_2\left( \frac{\sigma}{2} \right) + \epsilon, \end{aligned} \]

我们有，对于所有足够大的\(i\)

\[\frac{\log_q\left( \binom{n_i}{m_i} \times A_{s_i - m_i}(\mathcal{X}_i) \right)}{g(\mathcal{X}_i)} < \frac{\log_q\left( h(\mathcal{X}_i) \right)}{g(\mathcal{X}_i)}. \]

根据推论 \(7\)，存在\(q\)-ary \(\left[n_i, k_i, d_i\right]\)-线性编码，使得

此时 \(s\geq g\) 并不显然，但是在 \(q\) 充分大时是正确的。

\[k_i \geq s_i - g(\mathcal{X}_i) + 1 \quad d_i \geq n_i - m_i+1 \]

因此，

\[\liminf_{i \to \infty} \frac{d_i}{n_i} \geq \lim_{i \to \infty} \left( 1 - \frac{m_i}{n_i} \right) = \delta \]

并且

\[\begin{aligned} \liminf_{i \to \infty} \frac{k_i}{n_i} & \geq \lim_{i \to \infty} \frac{m_i - g(\mathcal{X}_i) + \left( s_i - m_i \right) + 1}{n_i} \\ & \geq 1 - \delta - \frac{1}{A} + \frac{\sigma}{A} \\ & = 1 - \delta - \frac{1}{A} \\ & + \frac{1}{A} h_q\left( 1 + A \cdot \log_q\left( \frac{q}{q-1} \right) - A \left( \log_q 2 \right) H_2(\delta) - \epsilon \right) \end{aligned} \]

让\(\epsilon\)趋于0，我们得到了所需的结果。

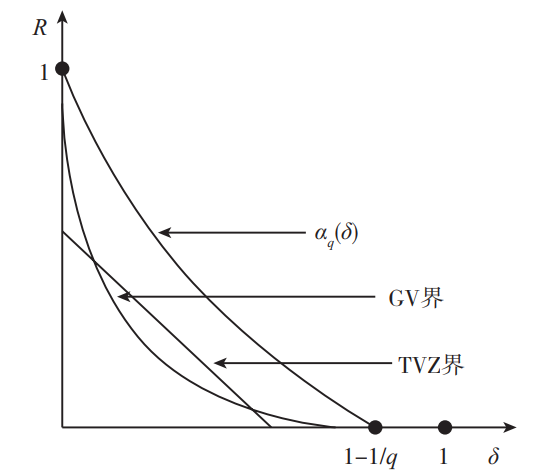
以下结果说明确实存在 \(\delta\) 使得定理 \(13\) 中的 \(1 + A \cdot \log_q \left( \frac{q}{q-1} - A \left( \log_q 2 \right) H_2(\delta) \right)\)位于区间\((0, \frac{2}{\sqrt{q} + 1})\)内，从而我们得到的改进式是对 GV 和 TVZ 界的实质性改进(而且是在 GV 界和 TVZ 界的交点附近)。

推论 14

设 \(q\) 为素幂。如果 \(R_G(\delta) > R_{GV}(\delta)\)，对于某个开区间中的所有 \(\delta\)，并且 \(0 < \delta_1 < \delta_2 < 1\) 是方程 \(R_G(x) = R_{\mathrm{GV}}(x)\) 的两个解，那么存在两个区间 \(\left(a_i, b_i\right) \subset (0,1)\)，对于 \(i=1,2\)，使得 \(\delta_i \in \left(a_i, b_i\right)\) 且

\[R(q, \delta) > \max \left\{ R_G(\delta), R_{\mathrm{GV}}(\delta) \right\} \]

对于任何 \(\delta \in \left(a_i, b_i\right)\) 成立。

上面推论的结果如图 1 所示。

证明：由于 \(\delta_i\) 是方程 \(R_G(x) = R_{\mathrm{GV}}(x)\) 的解，我们有

\[1 - \delta_i - \frac{1}{A(q)} = 1 - H_q(\delta_i) \]

即，

\[1 + A(q) \delta_i \log_q \frac{q}{q-1} - A(q)\left(\log_q 2\right) H_2(\delta_i) = 0 \]

考虑

\[\begin{aligned} 1 + & A(q) \log_q \frac{q}{q-1} - A(q)\left(\log_q 2\right) H_2(\delta_i) \\ = & 1 + A(q) \delta_i \log_q \frac{q}{q-1} - A(q)\left(\log_q 2\right) H_2(\delta_i) \\ & + A(q)(1 - \delta_i) \log_q \frac{q}{q-1} \\ = & A(q)(1 - \delta_i) \log_q \frac{q}{q-1} \\ \leq & (\sqrt{q}-1) \log_q \frac{q}{q-1} < \frac{2}{\sqrt{q}+1}. \end{aligned} \]

因此，\(1 + A(q) \log_q \frac{q}{q-1} - A(q)\left(\log_q 2\right) H_2(\delta_i)\) 位于区间 \((0, \frac{2}{\sqrt{q}+1})\) 中。因此

\[h_q\left(1 + A(q) \log_q \frac{q}{q-1} - A(q)\left(\log_q 2\right) H_2(\delta_i)\right) > 0 \]

这意味着

\[\begin{aligned} & R\left(q, \delta_i\right) - R_{\mathrm{GV}}\left(q, \delta_i\right) \\ & = R\left(q, \delta_i\right) - R_{\mathrm{TVZ}}\left(q, \delta_i\right) \\ & = \frac{1}{A(q)} h_q\left(1 + A(q) \log_q \frac{q}{q-1} - A(q)\left(\log_q 2\right) H_2(\delta_i)\right) > 0 \end{aligned} \]

由于 \(R(q, \delta)\)、\(R_{\mathrm{GV}}(q, \delta)\) 和 \(R_G(q, \delta)\) 都在包含 \(\delta_i\) 的开区间内连续存在，因此存在一个开区间 \(\left(a_i, b_i\right) \subset (0, 1)\)，使得 \(\delta_i \in \left(a_i, b_i\right)\) 且

\[R(q, \delta) > \max \left\{ R_G(\delta), R_{\mathrm{GV}}(\delta) \right\} \]

对于任何 \(\delta \in \left(a_i, b_i\right)\) 成立。这完成了证明。\(\square\)

推论 15

设 \(q \geq 49\) 为平方数。设 \(0 < \delta_1 < \delta_2 < 1\) 为方程 \(R_{\mathrm{TVZ}}(x) = R_{\mathrm{GV}}(x)\) 的两个解，那么存在两个区间 \(\left(a_i, b_i\right) \subset (0,1)\)，对于 \(i=1,2\)，使得 \(\delta_i \in \left(a_i, b_i\right)\) 且

\[R(q, \delta) > \max \left\{ R_{\mathrm{TVZ}}(\delta), R_{\mathrm{GV}}(\delta) \right\} \]

对于任何 \(\delta \in \left(a_i, b_i\right)\) 成立。

推论 16

设 \(q \geq (527 \times 27)^3\) 为立方数。设 \(0 < \delta_1 < \delta_2 < 1\) 为方程 \(R_G(x) = R_{\mathrm{GV}}(x)\) 的两个解，那么存在两个区间 \(\left(a_i, b_i\right) \subset (0,1)\)，对于 \(i=1,2\)，使得 \(\delta_i \in \left(a_i, b_i\right)\) 且

\[R(q, \delta) > \max \left\{ R_G(\delta), R_{\mathrm{GV}}(\delta) \right\} \]

对于任何 \(\delta \in \left(a_i, b_i\right)\) 成立。

附录

命题 \(8\) 的推导：
首先将分母展开为几何级数：

\[\frac{1}{(1-T)(1-qT)} = \sum_{n=0}^\infty \left( \sum_{k=0}^n q^k \right) T^n = \sum_{n=0}^\infty \frac{q^{n+1}-1}{q-1} T^n. \]

将 $ L(T) = \sum_{i=0}^{2g} a_i T^i $ 与分母级数相乘，得到：

\[Z(T) = \sum_{i=0}^{2g} a_i T^i \cdot \sum_{n=0}^\infty \frac{q^{n+1}-1}{q-1} T^n. \]

提取 $ T^t $ 项的系数 $ A_t $：

\[A_t = \sum_{i=0}^{\min(t, 2g)} a_i \cdot \frac{q^{t-i+1}-1}{q-1}. \]

将 $ i=0 $ 和 $ i=1 $ 的项单独处理：

\[A_t = \underbrace{a_0 \cdot \frac{q^{t+1}-1}{q-1}}_{i=0} + \underbrace{a_1 \cdot \frac{q^t-1}{q-1}}_{i=1} + \sum_{i=2}^t a_i \cdot \frac{q^{t-i+1}-1}{q-1}. \]

已知 $ a_0 = 1 $，且比较系数易知：

\[a_1 = A_1 - (1 + q). \]

将 $ a_0 $ 和 $ a_1 $ 代入表达式：

\[A_t = \frac{q^{t+1}-1}{q-1} + \left(A_1 - (1+q)\right) \cdot \frac{q^t-1}{q-1} + \sum_{i=2}^t a_i \cdot \frac{q^{t-i+1}-1}{q-1}. \]

最终得到：

\[A_t = \sum_{i=2}^t \frac{q^{t+1-i}-1}{q-1} a_i + \frac{q^t-1}{q-1} A_1 - \frac{q^t - q}{q-1}. \]

\(\square\)

推论 \(9\) 的推导：
由条件可知，$ T^{2g} L(1/T) $ 的根为 $ r_1, r_2, \dots, r_{2g} $，且每个根的绝对值满足 $ |r_j| = q^{1/2} $。因此，该多项式可表示为：

\[T^{2g} L(1/T) = \prod_{j=1}^{2g} (T - r_j). \]

将 $ T $ 替换为 $ 1/T $，两边乘以 $ T^{2g} $，得到：

\[L(T) = \prod_{j=1}^{2g} (1 - r_j T). \]

展开 $ L(T) $ 的表达式：

\[L(T) = \sum_{i=0}^{2g} (-1)^i e_i(r_1, \dots, r_{2g}) T^i, \]

其中 $ e_i(r_1, \dots, r_{2g}) $ 是第 $ i $ 个初等对称多项式，表示所有可能的 $ i $ 个不同根乘积之和。因此，系数为：

\[a_i = (-1)^i e_i(r_1, \dots, r_{2g}). \]

由于每个根的绝对值 $ |r_j| = q^{1/2} $，任意 $ i $ 个不同根乘积的绝对值为：

\[\left| \prod_{j \in S} r_j \right| = q^{i/2}, \quad \text{其中 } S \subseteq \{1, 2, \dots, 2g\}, \, |S| = i. \]

初等对称多项式 $ e_i $ 包含 $ \binom{2g}{i} $ 项，每项的绝对值不超过 $ q^{i/2} $。根据三角不等式：

\[|e_i(r_1, \dots, r_{2g})| \leq \sum_{S} \left| \prod_{j \in S} r_j \right| = \binom{2g}{i} q^{i/2}. \]

由于 $ |a_i| = |e_i(r_1, \dots, r_{2g})| $，代入上一步的估计：

\[|a_i| \leq \binom{2g}{i} q^{i/2}. \]

\(\square\)