0.4 有限域上代数曲线

代数闭域

定义 1 代数封闭

如果域\(k\)上的每一个多项式在\(k[x]\)中至少有一个根，则称\(k\)是代数封闭的。

例如， \(\mathbb{F}_2\)不是代数封闭的，因为\(x^2 + x + 1\)在\(\mathbb{F}_2\)上是不可约的。同样地， \(\mathbb{Q}\)和\(\mathbb{R}\)也不是代数封闭的，因为\(x^2 + 1\)在这些域上是不可约的。然而， \(\mathbb{C}\)是代数封闭的，这就是代数学基本定理。

模仿欧几里得证明素数有无穷多个的方法可以很容易的证明有限域\(\mathbb{F}\)不是代数封闭的，其上总存在不可约多项式。

给定一个域\(k\)，通常我们希望考察一个包含\(k\)且代数封闭的域。

定义 2 代数闭包

设\(k\)是一个域。 \(k\)的代数闭包是一个满足以下条件的域\(K\)，其中\(k \subseteq K\)：
\((1)\)\(K\)是代数封闭的；
\((2)\)若\(L\)是一个满足\(k \subseteq L \subseteq K\)且代数封闭的域，则有\(L = K\)。

换句话说， \(k\)的代数闭包是包含\(k\)的“最小”代数封闭域。存在以下定理：

定理 3 代数闭包的唯一性

每个域都有一个唯一的代数闭包（在同构意义下）。

由于这个定理，我们总是可以放心地谈论域\(k\)的代数闭包，并将其记作\(\bar{k}\)。例如， \(\overline{\mathbb{R}} = \mathbb{C}\)。另一方面，已知\(\pi\)不是任何在\(\mathbb{Q}\)上的多项式的根，因此\(\overline{\mathbb{Q}} \subset \mathbb{C}\)，但\(\overline{\mathbb{Q}} \neq \mathbb{C}\)。此外， \(\overline{\mathbb{F}}_4 = \overline{\mathbb{F}}_2\)，一般而言， \(\overline{\mathbb{F}}_{p^n} = \overline{\mathbb{F}}_p\)。

\(p\)是素数，考虑\(p\)元有限域\(\mathbb{F}_p\)，由于有限域的存在唯一性定理我们知道，有限域\(\mathbb{F}_{p^n}\)总是存在的，而且其生成元(不唯一)会给出一个\(\mathbb{F}_p\)上的\(n\)次不可约多项式。所以我们有\(\overline{\mathbb{F}_p}=\bigcup_{i=1}^{\infty}\mathbb{F}_{p^i}\)。

下述定理给出了代数封闭域的一个关键性质。

定理 4 代数闭域上多项式可完全分解

设\(k\)是一个代数封闭域， \(f(x) \in k[x]\)是一个次数为\(n\)的多项式。那么，存在\(u \in k^{\times} := k \backslash \{0\}\)和\(\alpha_1, \ldots, \alpha_n \in k\)（不一定不同），使得

\[f(x) = u(x - \alpha_1) \cdots (x - \alpha_n). \]

特别地，在计重数的情况下， \(f\)在\(k\)中恰有\(n\)个根。

证明： 对\(n\)归纳。

\((1)\)当\(n = 0\)时， \(f\)是常数，因此\(f \in k^{\times}\)。
\((2)\)现在假设所有次数为\(n\)的多项式都可以按定理的形式表示，考虑一个次数为\(n+1\)的多项式\(f(x) \in k[x]\)。由于\(k\)是代数封闭域， \(f\)必定有一个根\(\alpha\)。

由欧式除法算法， \(f(x)\)可以写成

\[f(x) = (x - \alpha) g(x), \]

其中\(g(x) \in k[x]\)的次数为\(n\)。根据归纳假设， \(g(x)\)可以按定理的形式表示，因此\(f(x)\)也可以写成所需的形式，从而证明了定理。
\(\square\)

曲线与射影平面

给定一个整数或有理数系数的多项式（即丢番图方程），数论中的一个基本问题是寻找该方程在整数、正整数或有理数中的解。例如，费马大定理断言，当\(n \geq 3\)时，方程

\[x^n + y^n = z^n \]

在正整数中没有解\((x, y, z)\)。寻找可以作为直角三角形边长的正整数\(a, b, c\)（即毕达哥拉斯三元组）的问题可以表述为寻找方程

\[a^2 + b^2 = c^2 \]

在正整数中的解。

通常，研究这些问题时，将方程从几何角度考虑或模某个素数\(p\)进行分析是十分有用的。如果\(f(x, y) = 0\)是一个二元多项式，那么该方程\(f(x, y) = 0\)定义了平面上的一条曲线\(C_f\)。这引出了对代数曲线以及有限域上代数曲线的研究。

在某个域\(k\)中满足方程\(f(x, y) = 0\)的解的集合记作\(C_f(k)\)。

简单的二元丢番图方程(简单到可以观察出一个平凡的解)有通用的被称为“有理直线法”的解法，从平凡的解点处作有理斜率的直线与二元丢番图方程联立，韦达定理保证了所得的另一个解是有理解。

如果我们希望找到两个二元多项式方程的同时解，那么我们实际上是在寻找两条曲线的交点。让我们来看一个具体的例子。取\(f(x, y) = y - x^2\)和\(g(x, y) = y - c\)，并考察不同\(c\)取值的情况。

如果我们取\(k = \mathbb{R}\)，可以绘制这两个方程的图像并观察交点。有时，它们恰好有两个交点，例如当\(c = 4\)时。如果\(c = 0\)，它们只有一个交点，而当\(c < 0\)时，它们没有交点！然而，如果我们注意到当\(c = 0\)时，两条曲线在交点处实际上是相切的，那么我们可以将该交点计算为一个重数为\(2\)的交点。此外，如果我们将域扩张到其代数闭包\(\bar{k} = \mathbb{C}\)，那么当\(c < 0\)时，我们实际上也能找到两个交点。更一般地，如果取形如\(y = mx + b\)的直线，则在\(\mathbb{R}\)上的交点个数可能是\(2\)、 \(1\)或\(0\)，与之前的情况类似：如果只有一个交点，则说明该直线与曲线相切；如果没有交点，那么在\(\mathbb{C}\)中我们可以找到两个交点。这样看来，曲线\(C_f\)和\(C_g\)总是会有恰好两个交点，至少在考虑重数并扩张到代数闭包的情况下。

但现在，如果我们用垂直直线\(g(x, y) = x - c\)替换原来的\(g\)，则无论\(c\)取何值，曲线和直线的交点都只有一个，并且该交点不是切点。即使扩展到\(\mathbb{C}\)，情况也不会有所改变。然而，我们仍然感觉如果正确计算(或者说正确定义)的话，任意一条直线和曲线\(C_f\)（其中\(f(x, y) = y - x^2\)）的交点数应该是\(2\)。

从直观上来看，其思想如下：曲线\(x = c\)和\(y = x^2\)还在“无穷远处”相交一次。更一般地，若\(f(x, y) \in k[x, y]\)，则称曲线\(C_f\)为仿射曲线。我们希望研究\(C_f\)的射影闭包\(\widehat{C_f}\)，这相当于“添加无穷远点”。为此，我们构造多项式

\[F(X, Y, Z) = Z^d f(X / Z, Y / Z) \in k[X, Y, Z] \]

其中\(d = \deg(f)\)。

例如，方程\(y^2 = x^3 + x + 1\)定义的曲线即为\(C_f\)，其中\(f(x, y) = y^2 - x^3 - x - 1\)。则其对应的射影化多项式为

\[F(X, Y, Z) = Z^3 \left( (Y/Z)^2 - (X/Z)^3 - (X/Z) - 1 \right) = Y^2 Z - X^3 - X Z^2 - Z^3。 \]

注意， \(F\)中出现的每个单项式的次数都恰好为\(3 = \deg(f)\)，构造\(F\)的过程实质上是对\(f\)进行大写变量替换并添加足够的\(Z\)使得每一项的次数均为\(3\)。这个多项式\(F\)称为\(f\)的齐次化（homogenization）。

现在我们来探讨：方程\(f(x, y) = 0\)的解\(\left(x_0, y_0\right)\)与方程\(F(X, Y, Z) = 0\)的解\(\left(X_0, Y_0, Z_0\right)\)之间有何联系？可以立即得到以下三个观察结果：

-\(f\left(x_0, y_0\right) = 0 \Longleftrightarrow F\left(x_0, y_0, 1\right) = 0\)。

• 对于任意\(\alpha \in k^{\times}\)，有：

\[ \begin{aligned} F(\alpha X, \alpha Y, \alpha Z) &= (\alpha Z)^d f(\alpha X / \alpha Z, \alpha Y / \alpha Z) \\ &= \alpha^d F(X, Y, Z) \end{aligned} \]

因此，若\(F\left(X_0, Y_0, Z_0\right) = 0\)，则对于所有的\(\alpha \in k^{\times}\)，也有\(F\left(\alpha X_0, \alpha Y_0, \alpha Z_0\right) = 0\)。

• 由于\(F\)是齐次的，必然有\(F(0,0,0) = 0\)。

由于第三点，我们希望忽略方程\(F = 0\)的平凡解\((0,0,0)\)。由于第二点，我们希望将解\(\left(X_0, Y_0, Z_0\right)\)与\((\alpha X_0, \alpha Y_0, \alpha Z_0)\)视为相同的解。这引出了以下定义：

定义 5 射影平面

设\(k\)为一个域，射影平面\(\mathbb{P}^2(k)\)定义为

\[\mathbb{P}^2(k):=\left(k^3 \backslash\{(0,0,0)\}\right) / \sim, \]

其中，若存在某个\(\alpha \in k^{\times}\)使得

\[X_1=\alpha X_0, \quad Y_1=\alpha Y_0, \quad Z_1=\alpha Z_0, \]

则称\(\left(X_0, Y_0, Z_0\right) \sim\left(X_1, Y_1, Z_1\right)\)。

为了强调\(\mathbb{P}^2(k)\)中的点是等价类，我们用记号

\[\left(X_0: Y_0: Z_0\right) \]

表示点\((X_0, Y_0, Z_0)\)在\(\mathbb{P}^2(k)\)中对应的等价类。

定义 6 射影闭包

设\(k\)为一个域， \(f(x, y) \in k[x, y]\)为次数为\(d\)的多项式， \(C_f\)为与\(f\)相关联的曲线。曲线\(C_f\)的射影闭包（projective closure）定义为

\[\widehat{C_f}:=\left\{\left(X_0: Y_0: Z_0\right) \in \mathbb{P}^2 \mid F\left(X_0, Y_0, Z_0\right)=0\right\}, \]

其中

\[F(X, Y, Z):=Z^d f(X / Z, Y / Z) \in k[X, Y, Z] \]

是\(f\)的齐次化（homogenization）。

通过乘以一个单位元，我们可以假设\(\mathbb{P}^2(k)\)中的点的最右侧非零坐标为\(1\)，因此有

\[\begin{gathered} \mathbb{P}^2(k)=\left\{\left(X_0: Y_0: 1\right) \mid X_0, Y_0 \in k\right\} \cup \\ \left\{\left(X_0: 1: 0\right) \mid X_0 \in k\right\} \cup \\ \{(1: 0: 0)\} \end{gathered} \]

任意满足\(Z_0=0\)的点\(\left(X_0: Y_0: Z_0\right)\)被称为无穷远点（point at infinity），其他所有点称为仿射点（affine）。

练习 7

考虑射影平面\(\mathbb{P}^2(\mathbb{R})\)。

\((1)\)证明在\(\mathbb{P}^2(\mathbb{R})\)中，无穷远点与\(\mathbb{R}^2\)中过原点的直线之间存在一一对应关系。

\((2)\)给定\(\mathbb{R}^2\)中一条不经过原点的直线，该直线的射影闭包上包含哪个无穷远点？

现在让我们回到我们的示例，并看看在\(\mathbb{P}^2\)中考虑交点会发生什么。我们有\(f(x, y) = y - x^2\)，因此

\[F(X, Y, Z) = YZ - X^2 \]

同样， \(g(x, y) = x - c\)，因此

\[G(X, Y, Z) = X - cZ \]

为了找到仿射交点，我们设\(Z=1\)，则有方程

\[Y - X^2 = 0 \]

以及

\[X = c \]

因此\(Y = c^2\)，唯一的仿射交点是\((c: c^2: 1)\)。

现在来看无穷远点： \(F(X, Y, 0) = -X^2\)，当且仅当\(X = 0\)时取零，因此我们得到\((0: 1: 0)\)是\(\widehat{C_f}\)上的点。由于\(G(X, Y, 0) = X\)，这个点显然也在\(\widehat{C_g}\)上。因此，我们看到如果在\(\mathbb{P}^2\)中考虑交点， \(\widehat{C_f}\)和\(\widehat{C_g}\)的交点恰好有两个。

令\(Z=0\)相当于只考虑次数最大的项，而根据我们的朴素直觉，无穷远(方向趋势)的信息都有次数最大的项主导，所以称\(Z=0\)的解为曲线的无穷远点。

事实上，我们有以下定理：

定理 8 （贝祖定理）

如果\(f, g \in k[x, y]\)是分别具有次数\(d\)和\(e\)的多项式，则\(C_f\)和\(C_g\)最多相交\(de\)个点。此外，当考虑重数时， \(\widehat{C_f}\)和\(\widehat{C_g}\)在\(\mathbb{P}^2(\bar{k})\)中恰好相交\(de\)个点。

例如，贝祖定理指出，由二次多项式定义的任意两条曲线，在适当地计数时恰好相交四个点。如果我们设\(f_1(x, y) = y - x^2\)和\(f_2(x, y) = (y - 2)^2 - (x + 2)\)，则我们可以绘制曲线\(C_{f_1}\)和\(C_{f_2}\)，发现它们在\(\mathbb{R}^2\)中恰好有四个交点。然而，如果我们将\(f_2\)替换为\(f_3 = y^2 - (x + 2)\)，则\(C_{f_1}\)和\(C_{f_3}\)在\(\mathbb{R}^2\)中只相交两个点。允许使用复数坐标时，我们可以找到另外两个交点。另一方面，即使在复数坐标下，曲线\(C_{f_1}\)和\(C_{f_4}\)（其中\(f_4(x, y) = y + x^2 - 2\)）也仅在两个点相交。如果我们进行齐次化操作，则可以看到\(\widehat{C_{f_1}}\)和\(\widehat{C_{f_4}}\)在点\((0: 1: 0)\)处相交。根据贝祖定理，这两条曲线在此点必须具有重数\(2\)。换句话说，曲线在点\((0: 1: 0)\)处是切线。

对于编码理论，人们通常只希望处理“良好的”曲线。既然我们已经决定将范围限制在平面曲线，那么我们需要的另一个限制是我们的曲线将是非奇异的，这是一个我们将在下面定义的概念。由于非奇异性与可微性密切相关，我们必须首先弄清楚在任意域\(k\)上求导意味着什么。

设\(k\)为一个域， \(f(x, y) \in k[x, y]\)是一个多项式。如果\(k = \mathbb{R}\)或\(\mathbb{C}\)，我们完全理解\(f\)关于\(x\)的偏导数\(f_x\)是什么。如果\(k\)是特征为\(p > 0\)的域，传统的极限定义就不再成立。然而，对于\(f(x, y) \in \mathbb{F}_q[x, y]\)，我们可以通过简单地声明熟悉的求导规则实际上就是定义来定义\(f\)关于\(x\)的形式偏导数\(f_x(x, y) \in k[x, y]\)。例如，如果\(f(x, y) = x^2 + y^3 + xy\)，那么在任何域\(k\)上都有\(f_x(x, y) = 2x + y\)和\(f_y(x, y) = 3y^2 + x\)。特别地，如果\(k = \mathbb{F}_2\)，则\(f_x(x, y) = y\)和\(f_y(x, y) = y^2 + x\)。另一方面，如果\(k = \mathbb{F}_3\)，则\(f_x(x, y) = 2x + y\)和\(f_y(x, y) = x\)。

定义 9 奇异点

设\(k\)为一个域， \(f(x, y) \in k[x, y]\)。如果点\((x_0, y_0) \in \bar{k} \times \bar{k}\)满足\(f(x_0, y_0) = 0\)且\(f_x(x_0, y_0) = 0\)和\(f_y(x_0, y_0) = 0\)，则称\((x_0, y_0)\)是曲线\(C_f\)的一个奇异点。如果曲线\(C_f\)没有奇异点，则称它是非奇异的。如果\(F(X, Y, Z)\)是\(f(x, y)\)的齐次化，则\((X_0: Y_0: Z_0) \in \mathbb{P}^2(\bar{k})\)是曲线\(\widehat{C_f}\)的奇异点，当且仅当该点在曲线上，并且所有偏导数在该点处为零，即：

\[\begin{aligned} F(X_0, Y_0, Z_0) &= 0, \\ F_X(X_0, Y_0, Z_0) &= 0, \\ F_Y(X_0, Y_0, Z_0) &= 0, \\ F_Z(X_0, Y_0, Z_0) &= 0. \end{aligned} \]

如果曲线\(\widehat{C_f}\)没有奇异点，则称它是非奇异的。

练习 10

设\(f(x, y) \in \mathbb{R}[x, y]\)，并假设\((0,0)\)是曲线\(C_f\)上的一个非奇异点。如果\(f_y(0,0) \neq 0\)，证明直线\(y = m x\)，其中\(m = -\frac{f_x(0,0)}{f_y(0,0)}\)，是\(C_f\)在点\((0,0)\)处的切线。如果\(f_y(0,0) = 0\)，证明直线\(x = 0\)是\(C_f\)在点\((0,0)\)处的切线。

一般来说，如果\(P\)是曲线\(C_f\)上的一个非奇异点，则通过\(P\)且斜率为\(-\frac{f_x(P)}{f_y(P)}\)的直线是\(C_f\)在\(P\)处的切线。如果\(f_y(P) = 0\)，则切线是通过\(P\)的垂直线。练习\(10\)已经证明了这一点（经过坐标变换后）。

如果定义\(9\)是合理的，那么可以预期，如果\(C_f\)是非奇异的，则\(\widehat{C_f}\)唯一可能的奇异点应该位于无穷远处。这一结论是正确的，并且可以通过\(f\)的齐次化定义和偏导数的链式法则得出。这主要是因为令\(Z=1\)这个操作可以与对\(x,y\)求偏导的操作交换以及齐次函数的欧拉定理。

直观而言，奇异点是曲线上切线未被良好定义的点，或者是曲线自身相交的点。以下是四个在\(\mathbb{R}\)上具有奇异点的曲线示例（分别为 tacnode（重结点）,node（结点）,cusp（尖点）,triple point（三重点））：

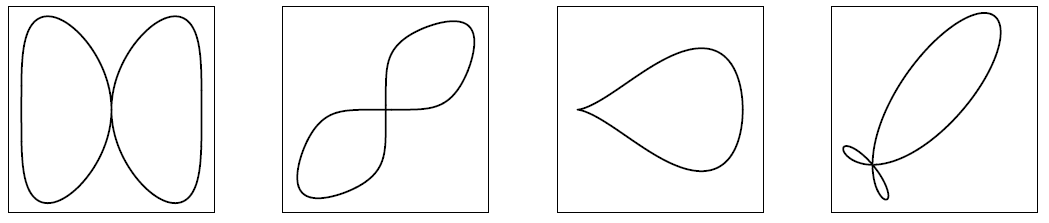
作为一个例子，我们考虑复数域上的曲线\(\widehat{C_f}\)，其中\(f(x, y) = -x^3 + y^2 + x^4 + y^4\)。计算其偏导数可得：

\[f_x(x, y) = -3x^2 + 4x^3 = x^2(-3 + 4x) \]

\[f_y(x, y) = 2y + 4y^3 = 2y(1 + 4y^2) \]

要使\((x_0, y_0)\)为奇异点，需要满足\(x_0 = 0\)或\(\frac{3}{4}\)，以及\(y_0 = 0, \frac{1}{2} i\)或\(-\frac{1}{2} i\)。经过快速检验，在\(6\)组可能的\((x_0, y_0)\)取值中，仅有\((0,0)\)在曲线上，因此它是唯一的仿射奇异点。

将\(f(x, y)\)齐次化得到：

\[F(X, Y, Z) = -X^3Z + Y^2Z^2 + X^4 + Y^4 \]

计算其偏导数：

\[F_X = -3X^2Z + 4X^3, \quad F_Y = 2YZ^2 + 4Y^3, \quad F_Z = -X^3 + 2YZ^2 \]

由于仿射奇异点已找到，我们仅需检查无穷远点。令\(Z = 0\)，则若\((X_0:Y_0:0)\)是奇异点，需要满足：

\[X_0^4 + Y_0^4 = X_0^3 = 4Y_0^3 = -X_0^3 = 0 \]

唯一可能的解是\(X_0 = Y_0 = 0\)，但这在\(\mathbb{P}^2\)中不可能成立，因为\(Z_0\)已经是\(0\)。因此，曲线\(\widehat{C_f}\)唯一的奇异点是\((0:0:1)\)。

顺带一提，前面展示的尖点（cusp）示例实际上对应的就是\(C_f\)。

可能会疑惑\(f\)在\((0,0)\)附近主要表现为\(f\approx -x^3 +y^2\),若写作\(y=\pm x^{\frac{3}{2}}\),则在\((0,0)\)处有统一的导数，从图像上观察也似乎是这样，两边的曲线都越来越扁地贴近\((0,0)\)，但是与平滑的曲线的最大不同是：在平滑曲线切线切点附近任取两个点连线的斜率与切线大差不差，但是尖点（cusp）却做不到这一点.

这一节的大多数内容都来自 Judy L. Walker 的《Codes and Curves》，这是一本很好的适合自学的读本，只不过错误较多而且年代较老。就像以下的练习题在原文中要求证明“非奇异的仿射平面曲线都是不可约的”，然而这是不对的，因为我们有反例\(x(x-1)=0\)是两条直线的并集，可约而且光滑。

练习 11

证明非奇异的射影平面曲线是不可约的。
证明： 设\(C=\mathcal{C}(f)\)和\(D=\mathcal{C}(g)\)是\(\mathbb{P}^2\)中的曲线

我们首先证明

\[\operatorname{Sing}(C) \cup \operatorname{Sing}(D) \cup (C \cap D) = \operatorname{Sing}(C \cup D) \]

左含于右是显然的，接下来，我们证明

\[\operatorname{Sing}(C \cup D) \subset \operatorname{Sing}(C) \cup \operatorname{Sing}(D) \cup (C \cap D) \]

如果\(p \in \operatorname{Sing}(C \cup D)\)，则至少\(p \in C\)或\(p \in D\)。若\(p \in C\)，则\(f(p) = 0\)，并且

\[\frac{\partial(fg)}{\partial x_i}(p) = f(p) \frac{\partial g}{\partial x_i}(p) + g(p) \frac{\partial f}{\partial x_i}(p) = g(p) \frac{\partial f}{\partial x_i}(p) \]

这意味着\(g(p) = 0\)或者对所有\(i\)都有\(\frac{\partial f}{\partial x_i}(p) = 0\)。因此， \(p\)要么属于\(C \cap D\)，要么是\(C\)的奇异点。

于是

\[\operatorname{Sing}(C \cup D) = \operatorname{Sing}(C) \cup \operatorname{Sing}(D) \cup (C \cap D) \]

如果曲线\(C\)可约也就是\(\mathbb{P}^2\)中两条曲线\(C_1\)和\(C_2\)的并集，则由贝祖定理它们必须在\(\mathbb{P}^2\)中相交。根据以上结论，它们的交点是\(C\)的奇异点。因此，若\(C\)是非奇异的，则它必须是不可约的。

练习 12

设\(k\)为一块域，对于任意的\(a, b \in k\)，考虑由多项式

\[F(X, Y, Z) = X^3 + a X Z^2 + b Z^3 - Y^2 Z \]

定义的射影平面曲线。若\(k\)的特征不为\(2\)和\(3\)时，求曲线何时是奇异的？（\(4a^3+27b^2\not ={0}\)）

亏格

从拓扑学的角度来看，每条非奇异曲线在\(\mathbb{C}\)上都可以作为\(\mathbb{R}^3\)中的一个曲面来实现。例如，椭圆曲线的方程具有形如\(y^2 = f(x)\)的形式，其中\(f(x)\)是一个无重根的三次多项式，它可以看作是\(\mathbb{R}^3\)中的一个环面（甜甜圈）。一般来说，每条非奇异曲线都可以表示为一个带有若干个孔的环面，而这些孔的数量被称为该曲线的拓扑亏格（topological genus）。特别地，椭圆曲线的亏格为\(1\)。

通常，如果\(f(x, y)\)是次数为\(d\)的多项式，并且射影化曲线\(\widehat{C_f}\)是非奇异的，那么\(C_f\)的拓扑亏格由以下公式给出：

\[g = \frac{(d-1)(d-2)}{2} \]

该公式称为 Plücker 公式。当然，这里的讨论并不严格，仅用于激发对以下定义的直觉：

定义 13 亏格

设\(f(x, y) \in k[x, y]\)是一个次数为\(d\)的多项式，且\(\widehat{C_f}\)是非奇异的，则\(C_f\)（或\(\widehat{C_f}\)）的亏格定义为

\[g := \frac{(d-1)(d-2)}{2} \]

换句话说，我们将亏格定义为\(\mathrm{Plücker}\)公式所给出的数值。尽管奇异曲线的亏格也可以被定义，我们在此不作讨论。

练习 13

对于以下每个多项式，验证其对应的射影平面曲线是非奇异的，然后求出该曲线的亏格。

\((1)\)\(f(x, y) = y^2 - p(x)\)，其中\(p(x) \in k[x]\)是次数为\(3\)且无重根的多项式，且\(k\)的特征不为\(2\)和\(3\)。（所有的三次多项式都可以变量替换成为\(x^3+ax+b\)的形式，无重根即\(4a^3+27b^2\not ={0}\)）

\((2)\)\(f(x, y) = y^2 + y - p(x)\)，其中\(p(x) \in k[x]\)是次数为\(3\)且无重根的多项式，且\(k\)的特征为\(2\)。

\((3)\)\(f(x, y) = x^{q+1} + y^{q+1} - 1 \in \mathbb{F}_{q^2}[x]\)，其中\(q\)是一个素数幂。

除子

定义 14 有理点

设\(k\)是一个域，令\(C\)是由方程\(F=0\)定义的射影平面曲线，其中\(F=F(X, Y, Z) \in k[X, Y, Z]\)是一个齐次多项式。对于任何包含\(k\)的域\(K\)，我们定义\(C\)上的一个 \(K\)-有理点 为满足\(F(X_0, Y_0, Z_0) = 0\)的点\((X_0: Y_0: Z_0) \in \mathbb{P}^2(K)\)。所有\(K\)-有理点的集合记作\(C(K)\)。其中， \(C(k)\)的元素称为次数为一的点，或简称有理点。

例如，若\(C\)由方程\(X^2 + Y^2 = Z^2\)定义，则\((3:4:5) = (3/5: 4/5:1) \in C(\mathbb{Q}) \subset C(\mathbb{C})\)，而\((3: 2i: \sqrt{5}) = (3/\sqrt{5}: 2i/\sqrt{5}: 1)\)和\((3: -2i: \sqrt{5}) = (3/\sqrt{5}: -2i/\sqrt{5}: 1)\)属于\(C(\mathbb{C})\)但不属于\(C(\mathbb{Q})\)。

回忆一下，复数域上的方程若在实数域上有复数解，则这些解必成共轭对。换句话说，如果\((x, y) = (a + b i, c + d i)\)满足多项式方程\(f(x, y) = 0\)，其中\(f(x, y) \in \mathbb{R}[x, y]\)，那么\((a - b i, c - d i)\)也必须是解。这本质上是因为复共轭是一个固定实数域\(\mathbb{R}\)的自同构。我们可以把\((a + b i, c + d i)\)和\((a - b i, c - d i)\)视为\(C_f\)上的同一个点，但该点在\(\mathbb{R}\)上的次数为二（唯一分解式中会出现二次的不可约多项式分量）。现在，我们将这一思想精确定义到有限域的情形。

假设\(k=\mathbb{F}_q\)是一个有限域，并取\(n \geq 1\)。我们知道在同构意义下，存在唯一的具有\(q^n\)个元素的域\(K=\mathbb{F}_{q^n}\)。此外， \(\mathbb{F}_q \subset \mathbb{F}_{q^n}\)，并且存在\(\mathrm{Frobenius}\)自同构\(\sigma_{q, n}: \mathbb{F}_{q^n} \to \mathbb{F}_{q^n}\)，其作用由

\[\sigma_{q, n}(\alpha) = \alpha^q \]

给出。如果\(C\)是定义在\(\mathbb{F}_q\)上的射影平面曲线，则该映射可作用于\(C\left(\mathbb{F}_{q^n}\right)\)的元素，使其变换为

\[\sigma_{q, n}\left(\left(X_0: Y_0: Z_0\right)\right) = \left(X_0^q: Y_0^q: Z_0^q\right) \]

类似地，如果\(C\)是仿射曲线，并且\(\left(x_0, y_0\right) \in C\left(\mathbb{F}_q\right)\)，则定义

\[\sigma_{q, n}\left(\left(x_0, y_0\right)\right) = \left(x_0^q, y_0^q\right) \]

定义 15 点类、次数

设\(C\)是一个非奇异射影平面曲线。在\(\mathbb{F}_q\)上，次数为\(n\)的点类指的是一个集合

\[P=\left\{P_0, \ldots, P_{n-1}\right\} \]

其中\(P_i\)是\(C\left(\mathbb{F}_{q^n}\right)\)中的\(n\)个不同的点，并且满足

\[P_i = \sigma_{q, n}^i\left(P_0\right), \quad \text{对于 } i=1, \ldots, n-1. \]

可以看出，素子域中的点都是一次点，我们之前的说法也符合这个定义。
现行的教材里更常见的叫法是把一个点类称作一个素除子

不难看出，如果\(C\)和\(C'\)是由次数分别为\(d\)和\(e\)的多项式在\(\mathbb{F}_q\)上定义的曲线，那么根据贝祖定理，它们在\(\mathbb{P}^2\left(\overline{\mathbb{F}}_q\right)\)中的\(d e\)个交点可以进行划分然后视作在\(\mathbb{F}_q\)上具有不同次数的点类，并且这些点的次数之和等于\(d e\)。

作为具有高次点的曲线的一个示例，设\(C_0\)是定义在\(\mathbb{F}_3\)上的射影平面曲线，它对应的仿射方程为

\[y^2 = x^3 + 2x + 2. \]

显然\(C_0\)是非奇异的，并且它的亏格（genus）为\(1\)。
通过代入\(x=0,1,2\)，我们可以看出\(C\)没有定义在\(\mathbb{F}_3\)上的仿射有理点。然而，将方程齐次化得到

\[Y^2Z = X^3 + 2XZ^2 + 2Z^3. \]

可以看出，它在无穷远处有一个唯一的点

\[P_{\infty} := (0:1:0). \]

因此，该曲线在\(\mathbb{F}_3\)上的点集为

\[C_0\left(\mathbb{F}_3\right) = \{P_{\infty}\}. \]

由于\(t^2+1\)在\(\mathbb{F}_3\)上是不可约的，我们可以写\(\mathbb{F}_9 = \mathbb{F}_3[t] / (t^2+1)\)。设\(\alpha\)为对应于\(t\)的\(\mathbb{F}_9\)元素，则有

\[\mathbb{F}_9 = \{ a + b \alpha \mid a, b \in \mathbb{F}_3 \} \]

其中\(\alpha^2 = -1 = 2\)。经过一些计算，我们得到

\[C_0(\mathbb{F}_9) = \{ (0: \alpha: 1), (0: 2 \alpha: 1), (1: \alpha: 1), (1: 2 \alpha: 1), (2: \alpha: 1), (2,2 \alpha: 1), P_{\infty} \} \]

\(\mathrm{Frobenius}\)自同态\(\sigma_{3,2}: \mathbb{F}_9 \to \mathbb{F}_9\)满足\(\sigma_{3,2}(\alpha) = \alpha^3 = \alpha \cdot \alpha^2 = 2 \alpha\)，因此我们可以写

\[C_0(\mathbb{F}_9) = Q_1 \cup Q_2 \cup Q_3 \cup \{ P_{\infty} \} \]

其中

\[Q_1 = \{(0: \alpha: 1), (0: 2 \alpha: 1)\}, \quad Q_2 = \{(1: \alpha: 1), (1: 2 \alpha: 1)\}, \quad Q_3 = \{(2: \alpha: 1), (2: 2 \alpha: 1)\} \]

是\(C_0\)上仅有的三个次数为二的点。

很容易证明此时\(\epsilon:\alpha\rightarrow 2\alpha\)是\(\mathbb{F}_9\)上的一个域自同构。并不是所有方程定义的曲线上的点都如此有规律，这里的规律本质上是因为\(x^3+2x+x=x(x+1)(x+2)+2\),所以不论\(x\)代入\(0,1,2\)中的哪一个，所要解的关于\(y\)的方程是同一个。并且计算很容易得出代入其他值此方程在\(\mathbb{F}_9\)上是无解的。

类似地，我们写

\[\mathbb{F}_{27} = \mathbb{F}_3[t] / (t^3 + 2t + 2) \]

设\(\omega\)为对应于\(t\)的\(\mathbb{F}_{27}\)元素，则有

\[\mathbb{F}_{27} = \{ a + b \omega + c \omega^2 \mid a, b, c \in \mathbb{F}_3 \} \]

且\(\omega^3 = -2 - 2\omega = 1 + \omega\)。于是我们得到

\[\begin{aligned} C_0(\mathbb{F}_{27}) = \{ & (\omega: 0: 1), (1+\omega: 0: 1), (2+\omega: 0: 1), (2 \omega: 1: 1), (2+2 \omega: 1: 1), (1+2 \omega: 1: 1), \\ & (2 \omega: 2: 1), (2+2 \omega: 2: 1), (1+2 \omega: 2: 1), (2 \omega^2: 1+\omega^2: 1), \\ & (2+\omega+2 \omega^2: 2+2 \omega+\omega^2: 1), (2+2 \omega+2 \omega^2: 2+\omega+\omega^2: 1), (2 \omega^2: 2+2 \omega^2: 1), \\ & (2+\omega+2 \omega^2: 1+\omega+2 \omega^2: 1), (2+2 \omega+2 \omega^2: 1+2 \omega+2 \omega^2: 1), \\ & (1+2 \omega^2: 1+\omega^2: 1), (\omega+2 \omega^2: 2+2 \omega+\omega^2: 1), (2 \omega+2 \omega^2: 2+\omega+\omega^2: 1), \\ & (1+2 \omega^2: 2+2 \omega^2: 1), (\omega+2 \omega^2: 1+\omega+2 \omega^2: 1), (2 \omega+2 \omega^2: 1+2 \omega+2 \omega^2: 1), \\ & (2+2 \omega^2: 1+\omega^2: 1), (1+\omega+2 \omega^2: 2+2 \omega+\omega^2: 1), (1+2 \omega+2 \omega^2: 2+\omega+\omega^2: 1), \\ & (2+2 \omega^2: 2+2 \omega^2: 1), (1+\omega+2 \omega^2: 1+\omega+2 \omega^2: 1), (1+2 \omega+2 \omega^2: 1+2 \omega+2 \omega^2: 1), P_{\infty} \} \end{aligned} \]

同样的，我们很容易证明映射\(\epsilon_1:\omega\rightarrow 1+\omega\)和\(\epsilon_2:\omega \rightarrow 2+\omega\)是\(\mathbb{F}_{27}\)上的域自同构。（很容易观察出是加法和乘法同态，然后算\(\mathrm{ker}\)证明单射即可。当然直接用\(\mathrm{Frobenius}\)映射的结论也可以。）但是哪怕把自同构映射搞清楚，计算所有的点这种事仍然很麻烦，因为没有好用简明的手段去判别有限域上的不可约多项式（比如这里的\(x^3+2x+2=\omega^2\)），当然我们可以直接交给计算机，比较系数取等得到线性方程组后求解，这对计算机来说轻而易举。

\(\mathrm{Frobenius}\)自同态\(\sigma_{3,3}: \mathbb{F}_{27} \to \mathbb{F}_{27}\)满足\(\sigma_{3,3}(\omega) = \omega^3 = 1 + \omega\)，因此我们可以写

\[C_0(\mathbb{F}_{27}) = R_1 \cup R_2 \cup \cdots \cup R_9 \cup \{ P_{\infty} \} \]

其中\(R_1, \dots, R_9\)是\(C_0\)上的九个次数为三的点。例如，我们可以取

\[R_1 = \{ (\omega: 0: 1), \sigma_{3,3}(\omega: 0: 1), \sigma_{3,3}^2(\omega: 0: 1) \} = \{ (\omega: 0: 1), (1+\omega: 0: 1), (2+\omega: 0: 1) \} \]

练习 16

设\(C\)是由方程

\[Y^q Z + Y Z^q = X^{q+1} \]

在域\(\mathbb{F}_{q^2}\)上定义的射影平面曲线，其中\(q\)是素数的幂。称\(C\)为Hermitian 曲线。

\((1)\)证明\(C\)是非奇异的，并计算\(C\)的亏格。

\((2)\)设\(q=2\)，求出\(C\left(\mathbb{F}_4\right)\)。（\((0,0,1),(0,1,1),(0,t,1),(0,1+t,1),(t,t,1),(t,1+t,1),(1+t,t,1),(1+t,1+t,1),(0,1,0)\)）

\((3)\)对于任意素数的幂\(q\)，证明\(C\)在无穷远处有唯一一个点。

\((4)\)同样对于任意素数的幂\(q\)，证明\(\# C\left(\mathbb{F}_{q^2}\right) = q^3 + 1\)。（有限域\(\mathbb{F}_{q^n}\)的唯一性，作过一次二次扩张后不再有二次不可约多项式）

我们之前提到，如果\(C\)和\(C'\)是定义在\(\mathbb{F}_q\)上的两个射影平面曲线，分别由次数为\(d\)和\(e\)的多项式所定义，那么它们在代数闭包\(\overline{\mathbb{F}}_q\)上的交点进行划分后可视为一些由同次点构成的点类，点类的代表元为\(P_1, P_2, \dots, P_{\ell}\)，这些点在\(\mathbb{F}_q\)上具有不同（可能相同）的次数。如果某个交点的交点重数大于\(1\)，则该点会在计数时重复出现。此外，我们有

\[d e = r_1 + r_2 + \cdots + r_{\ell} \]

其中\(r_i\)是点\(P_i\)在\(\mathbb{F}_q\)上的次数。为了表达这一事实，我们可以写

\[C \cap C' = P_1 + \cdots + P_{\ell} \]

并称\(C \cap C'\)为\(C\)和\(C'\)的交除子（intersection divisor）。基于这一动机，我们给出如下定义：

定义 17 除子

设\(C\)是定义在\(\mathbb{F}_q\)上的一条曲线。在\(\mathbb{F}_q\)上， \(C\)上的一个除子（divisor）是定义在\(C\)上所有点（不限次数，也就是代数闭包上的）集合上的自由阿贝尔群的一个元素。因此，每个除子都可以表示为

\[D = \sum n_Q Q \]

其中\(n_Q\)是整数， \(Q\)是\(C\)上的某个点（不限次数）。如果对所有\(Q\)都有\(n_Q \geq 0\)，则称\(D\)是有效的（effective），并记作\(D \geq 0\)。我们定义除子\(D = \sum n_Q Q\)的次数（degree）为\(\operatorname{deg} D = \sum n_Q \operatorname{deg} Q\)。除子\(D = \sum n_Q Q\)的支撑集（support）定义为\(\operatorname{supp} D = \{ Q \mid n_Q \neq 0 \}\)。最后，定义\(v_Q(D)：=n_Q\),通常叫做除子\(D\)在点（类）\(Q\)处的赋值。

注意到， \(D\)的支撑集始终是一个有限集合，上述交除子\(C \cap C'\)是一个次数为\(de\)的有效除子。

现在回到我们的例子，其中\(C_0\)是定义在\(\mathbb{F}_3\)上的射影平面曲线，与仿射方程\(y^2 = x^3 + 2x + 2\)对应。若设\(D = 5 P_{\infty} - 2 Q_3 + 7 R_1\)，则\(D\)是\(C_0\)在\(\mathbb{F}_3\)上的一个除子，其次数为\(5(1) - 2(2) + 7(3) = 22\)，支撑集为\(\{P_{\infty}, Q_3, R_1\}\)。注意， \((0: \alpha: 1) + (\omega: 0: 1)\)不是\(C_0\)在\(\mathbb{F}_3\)上的除子，因为\((0: \alpha: 1)\)和\((\omega: 0: 1)\)不是\(C_0\)在\(\mathbb{F}_3\)上的点。

定义 18 有理函数域

设\(\mathbb{F}_q(X, Y, Z)\)是定义在域\(\mathbb{F}_q\)上的光滑射影平面曲线\(C\)上的多项式，则\(C\)上的有理函数域定义为：

曲线上的多项式指得是定义域是这个曲线上的点的多项式,形式上就是\(\mathbb{F}_q(X, Y, Z)\)再商掉曲线的定义方程,但是此时还不能称之为多项式函数，稍微思考就可以发现，射影曲线上的多项式函数只能按下面的这种方式定义。

\[\mathbb{F}_q(C) := \left( \left\{ \frac{g(X, Y, Z)}{h(X, Y, Z)} \,\middle|\, \begin{array}{c} g, h \in \mathbb{F}_q[X, Y, Z] \\ \text{均为齐次多项式} \\ \text{且次数相同} \end{array} \right\} \cup \{0\} \right) \Big/ \sim \]

其中， \(g/h \sim g'/h'\)当且仅当\(g h' - g' h \in \langle F \rangle \subset \mathbb{F}_q[X, Y, Z]\)。

显然\(\mathbb{F}_q(C)\)确实是一个域，并且它包含\(\mathbb{F}_q\)作为其子域。

再次回到定义在\(\mathbb{F}_3\)上的曲线\(C_0\)的例子，我们有

\[F(X, Y, Z) = Y^2 Z - X^3 - 2 X Z^2 - 2 Z^3. \]

我们可以看到， \(\frac{X^2}{Z^2}\)和\(\frac{Y^2+X Z+Z^2}{X Z}\)在\(\mathbb{F}_3(C_0)\)中是相同的元素，因为在\(\mathbb{F}_3[X, Y, Z]\)中有：

\[(X^2)(X Z) - (Z^2)(Y^2+X Z+Z^2) = 2Z (Y^2 Z - X^3 - 2 X Z^2 - 2 Z^3). \]

现在回到一般情形，设\(C\)是定义在\(\mathbb{F}_q\)上的射影平面曲线，并且设\(f := g / h \in \mathbb{F}_q(C)\)。根据贝祖定理，由\(g=0\)和\(h=0\)定义的曲线各自与\(C\)在\(\mathbb{P}^2(\bar{k})\)中恰好相交于\(de\)个点，其中\(d\)是定义\(C\)的多项式的次数，而\(e = \deg g = \deg h\)。

定义 19 有理函数的除子

设\(C\)是定义在\(\mathbb{F}_q\)上的曲线，且设\(f := g / h \in \mathbb{F}_q(C)\)。则\(f\)的除子定义为

\[\operatorname{div}(f) := \sum P - \sum Q, \]

其中\(\sum P\)是交除子\(C \cap C_g\)，而\(\sum Q\)是交除子\(C \cap C_h\)。

设\(f = g / h\)是\(C\)上的有理函数。直观地看， \(C\)与由\(g = 0\)定义的曲线的交点是\(f\)的零点，而\(C\)与由\(h = 0\)定义的曲线的交点是\(f\)的极点，因此我们可以将\(\operatorname{div}(f)\)视为“\(f\)的零点减去极点”。由于

\[\operatorname{deg}(C \cap C_g) = \operatorname{deg}(C \cap C_h) = d e, \]

所以

\[\operatorname{deg} \operatorname{div}(f) = 0. \]

直观上来说， \(f\)的零点数与极点数相等。注意，如果某个点\(P\)同时出现在\(C \cap C_g\)和\(C \cap C_h\)中，则会发生某种抵消。特别地，只有当在抵消后\(P\)仍然以正（或负）系数出现在\(\operatorname{div}(f)\)中时， \(P\)才被认为是\(f\)的零点（或极点）。此外，常值函数\(f \in \mathbb{F}_q \subset \mathbb{F}_q(C)\)的除子恒为\(0\)。

由于有理函数实际上是等价类，我们需要确保\(\operatorname{div}(f)\)的定义不依赖于\(f\)所属等价类的代表元。这一点是成立的，我们先通过具体示例来说明这一点顺便帮助读者熟悉相关的运算，稍后再给出证明。在定义在\(\mathbb{F}_3\)上的曲线

\[C_0: Y^2 Z - X^3 - 2 X Z^2 - 2 Z^3 = 0 \]

上，我们需要计算\(C_0\)与以下曲线的交除子：

\[X^2 = 0, \quad Z^2 = 0, \quad Y^2 + Z^2 + X Z = 0, \quad X Z = 0. \]

对于交点\(\left(X_0: Y_0: Z_0\right)\)，它必须满足\(X_0 = 0\)且

\[Z_0(Y_0^2 - 2 Z_0^2) = 0. \]

我们取

\[\mathbb{F}_9 = \mathbb{F}_3[t] / (t^2 + 1), \]

并令\(\alpha\)表示对应于\(t\)的元素，则有\(\alpha^2 = -1 = 2\)，因此多项式\(Y_0^2 - 2 Z_0^2\)分解为

\[(Y_0 - \alpha Z_0)(Y_0 + \alpha Z_0). \]

这意味着交点\(\left(X_0: Y_0: Z_0\right)\)必须满足\(X_0 = 0\)且以下三个条件之一成立：

\[Z_0 = 0, \quad Y_0 = \alpha Z_0, \quad Y_0 = 2 \alpha Z_0. \]

因此，在\(\mathbb{P}^2(\mathbb{F}_9)\)中的三个交点是

\[P_{\infty}, \quad (0: \alpha: 1), \quad (0: 2\alpha: 1). \]

由于\(\{(0: \alpha: 1), (0: 2\alpha: 1)\}\)对应于之前的点\(Q_1\)，所以直线\(X = 0\)与\(C_0\)的交除子为

\[P_{\infty} + Q_1. \]

因此，“双直线”\(X^2 = 0\)与曲线\(C_0\)的交除子为

\[2 P_{\infty} + 2 Q_1. \]

注意，该除子的次数确实为

\[6 = 2 \cdot 3. \]

利用同样的思路和办法，读者自行求出\(C_0\)与由\(Z^2 = 0\)定义的曲线的交除子为\(6 P_{\infty}\)。证明\(C_0\)与由\(XZ = 0\)定义的曲线的交除子为\(4 P_{\infty} + Q_1\)。

\(C_0\)与由\(Y^2 + Z^2 + XZ = 0\)定义的曲线的交点计算稍显复杂，因为该曲线不仅仅是两条直线的并。然而，该曲线唯一的无穷远点是\((1:0:0)\)，而\(C_0\)唯一的无穷远点是\(P_{\infty} = (0:1:0)\)，因此两条曲线在无穷远处没有交点。因此，我们可以假设\(Z =1\)得到\(C_0\)的仿射部分，其方程为\(y^2 - x^3 - 2x - 2 = 0\)，以及另一条曲线，其方程为\(y^2 + 1 + x = 0\)。

尽管我们仍然没有得到两条直线的乘积形式，但可以从第二个方程中解出\(x = -(1 + y^2)\)并代入第一个方程，得到

\[0 = y^2 + (1 + y^2)^3 + 2(1 + y^2) + 2 = y^6 + 1 = (y^2 + 1)^3 = (y - \alpha)^3(y + \alpha)^3. \]

因此，这两条曲线在\(Q_1\)处的交点重数为\(3\)，故交除子为\(3Q_1\)。

结合上述内容，我们得到：

\[\operatorname{div}\left(X^2 / Z^2\right) = \left(2 P_{\infty} + 2 Q_1\right) - 6 P_{\infty} = 2 Q_1 - 4 P_{\infty}, \]

\[\operatorname{div}\left(\left(Y^2 + XZ + Z^2\right) / XZ\right) = 3Q_1 - \left(4 P_{\infty} + Q_1\right) = 2 Q_1 - 4 P_{\infty}, \]

这两个除子确实相等。

接下来我们给出证明。

命题 20 射影曲线上的有理函数的除子不依赖于代表元的选取。

证明： 设\(\frac{a}{b}=\frac{c}{d}\in \mathbb{F}_q(C)~i.e.~ad-bc\in \braket{F}\),其中\(F\)是射影曲线\(C\)的定义式（齐次多项式），即需证\(C\cap C_a-C\cap C_b=C\cap C_c-C\cap C_d\)，显然\(C\cap C_a +C\cap C_d=C\cap C_{ad}\),于是仅需证\(C\cap C_{bc+FG}=C\cap C_{bc}\)，这是显然成立的. \(\square\)

还是回到上述的例子，我们考察过曲线\(X^2=0\)与\(C_0\)的交除子为\(2P_{\infty}+2Q_1\),显然也有 曲线\(X^3=0\)与\(C_0\)的交除子为\(3P_{\infty}+3Q_1\)。现在我们考虑曲线\(X^2+X^3=0\)与\(C_0\)的交除子，并且只考虑交除子中\(X=0\)的那些点，会发现仍为\(2P_{\infty}+2Q_1\)。基于此，我们有如下很容易理解的命题：

命题 21 赋值不等式

\(v_P(C\cap C_{a+b})\geq \mathrm{min}\{v_P(C\cap C_{a}),v_P(C\cap C_b)\}\)

证明思路是这样的，基于上述的例子，我们可以直接得出当\(v_P(C\cap C_{a+b})\geq 1\)时该命题是正确的，然后用反证法很容易证明\(=0\)的情况。

现在我们已经了解了除子、有理函数以及有理函数的除子，接下来可以给出下一个定义。

定义 22 黎曼罗赫空间

设\(D\)是定义在域\(\mathbb{F}_q\)上的非奇异射影平面曲线\(C\)上的除子，则与\(D\)相关联的有理函数空间（也叫做黎曼罗赫空间）定义为

\[L(D) := \left\{ f \in \mathbb{F}_q(C) \mid \operatorname{div}(f) + D \geq 0 \right\} \cup \{0\}. \]

这里需要做几点说明。首先，根据命题\(22\)很容易证明\(L(D)\)是一个\(\mathbb{F}_q\)上的向量空间。事实上，它是有限维的，但证明这一点较为困难。

为了区分除子\(D\)中的正系数和负系数的点（类），我们可以将其写成\(D = D_{\text{pos}} - D_{\text{neg}}\)，其中\(D_{\text{pos}}\)和\(D_{\text{neg}}\)是有效除子。同样，我们可以将\(\operatorname{div}(f)\)也表示为两个有效除子的差，即

\[\operatorname{div}(f) = (\text{零点的除子}) - (\text{极点的除子}). \]

因此，我们有

\[\operatorname{div}(f) + D = \left(D_{\text{pos}} - (\text{极点的除子})\right) + \left((\text{零点的除子}) - D_{\text{neg}}\right). \]

直观地说， \(f \in \mathbb{F}_q(C)\)属于\(L(D)\)当且仅当\(f\)具有“足够多”的零点“覆盖”\(D_{neg}\)，并且“极点不会太多”不“超过”\(D_{pos}\)。

下面这个命题很容易证明但是确实是常用到的。

命题 23 设\(D\)是定义在域\(\mathbb{F}_q\)上的非奇异射影平面曲线\(C\)上的除子。

\((1)\)证明如果\(\operatorname{deg} D \leq 0\)，则\(L(D) = \{0\}\)。
\((2)\)证明\(\mathbb{F}_q \subset L(D)\)当且仅当\(D \geq 0\)。

我们以黎曼–罗赫定理的陈述作为本节的结尾：

定理 24（黎曼–罗赫定理）

设\(C\)是定义在域\(\mathbb{F}_q\)上的亏格为\(g\)的非奇异射影平面曲线，且\(D\)是\(C\)上的除子。则

\[\operatorname{dim} L(D) \geq \operatorname{deg} D + 1 - g. \]

此外，若\(\operatorname{deg} D > 2g - 2\)，则

\[\operatorname{dim} L(D) = \operatorname{deg} D + 1 - g. \]

---

让我们最后一次回到开始的例子。我们考虑定义在\(\mathbb{F}_3\)上的曲线\(C_0\)，其方程为

\[Y^2 Z - X^3 - 2 X Z^2 - 2 Z^3 = 0. \]

回忆一下， \(Q_1\)是\(C_0\)上次数为\(2\)的点\(\{(0: \alpha: 1), (0: 2\alpha: 1)\}\)，其中\(\alpha^2 + 1 = 0\)。我们可以将上述结果整理在一起，得到有理函数\(X / Z\)在\(C_0\)上的除子为

\[\operatorname{div}(X / Z) = Q_1 - 2 P_{\infty}. \]

此外，很容易验证，有理函数\(Y / Z\)的除子为

\[\operatorname{div}(Y / Z) = R_1 - 3 P_{\infty}, \]

其中\(R_1\)是\(C_0\)上次数为\(3\)的点集

\[\{(\omega: 0: 1), (1+\omega: 0: 1), (2+\omega: 0: 1)\} \]

且\(\omega \in \mathbb{F}_{27}\)满足\(\omega^3 = 1 + \omega\)。因此，对于任意\(i, j \geq 0\)，我们有

\[\operatorname{div}\left(X^i Y^j / Z^{i+j}\right) = i Q_1 + j R_1 - (2i + 3j) P_{\infty}. \]

现在，设\(r\)为正整数，并定义除子\(D = r P_{\infty}\)。由黎曼–罗赫定理，

\[\operatorname{dim} L(D) = \operatorname{deg}(D) + 1 - g = r + 1 - 1 = r. \]

当\(r = 1\)时，由命题\(23\)可知\(L(D) = \mathbb{F}_q\)，因此\(\{1\}\)是\(L(D)\)的一组基。
当\(r = 2\)时，由上一段可知\(X / Z \in L(D)\)，且显然\(\{1, X / Z\}\)线性无关，因此它是\(L(D)\)的一组基。
当\(r = 3\)时，我们有

\[\operatorname{div}(Y / Z) + D = R_1 - 3 P_{\infty} + 3 P_{\infty} = R_1 \geq 0, \]

因此\(\{1, X / Z, Y / Z\}\)是\(L(D)\)的一组基。