2.6 二元里德-米勒码

本章介绍一类二元线性码, 它是由里德 $(Reed)$ 和米勒$(Muller)$ 于 $1954$ 年独立给出的,今后简记为 $\mathrm{RM}$ 码. 这种二元线性码的构造需要布尔函数的一些知识.

定义 1 设 \(m\) 为正整数. 一个 \(m\) 元布尔函数 \(f=f\left(x_1, \cdots, x_m\right)\) 是由 \(F_2^m\) 到 \(F_2\) 的映射,即 \(m\) 个变量 \(x_1, \cdots, x_m\) 均取值于 \(F_2\), 并且函数值也属于 \(F_2\). 换句话说, \(m\) 元布尔函数是一个映射

\[f=f\left(x_1, \cdots, x_m\right): F_2^m \longrightarrow F_2, \]

其中, 对每个 \(\left(a_1, \cdots, a_m\right) \in F_2^m\), 函数 \(f\) 在 \(\left(a_1, \cdots\right.\), \(\left.a_m\right)\) 的取值记成 \(f\left(a_1, \cdots, a_m\right) \in F_2\). 由于 \(F_2^m\) 中向量的个数为 \(2^m\), 而 \(f\) 在每个向量的取值均彼此独立地可取 \(1\) 或 \(0\) , 所以 \(m\) 元布尔函数共有 \(2^{2^m}\) 个. 当 \(m\) 较大时, \(m\) 元布尔函数有很多个.
例如,一元布尔函数 \(f(x)\) 共有 \(2^{2^1}=4\) 个,它们是:

\[\begin{aligned} & f(0)=f(1)=0, 即 f(x) \equiv 0, \\ & f(0)=f(1)=1, 即 f(x) \equiv 1, \\ & f(0)=0, f(1)=1, 即 f(x)=x, \\ & f(0)=1, f(1)=0, 即 f(x)=x+1 . \end{aligned} \]

所以一元布尔函数 \(f(x)\) 都可表示成 \(x\) 的多项式. 注意 \(f(x)=x^2\) 和 \(g(x)=x\) 是不同的多项式, 但是它们为同一个布尔函数, 因为 \(f(0)=\) \(g(0)=0, f(1)=g(1)=1\), 即对 \(F_2\) 中每个元素 \(a, f(x)\) 和 \(g(x)\) 的函数值都相等.
一般地, 对于每个关于 \(x_1, \cdots, x_m\) 的多项式 \(f\left(x_1, \cdots, x_m\right)\) (系数均属于 \(F_2\)), 如果把其中出现的所有 \(x_i^l(l \geqslant 1)\) 均改成 \(x_i\), 所得的多项式 \(g\left(x_1, \cdots, x_m\right)\) 和 \(f\left(x_1, \cdots, x_m\right)\) 是同一个 \(m\) 元布尔函数. 而新的多项式 \(g\left(x_1, \cdots, x_m\right)\) 有形式

\[\begin{aligned} g\left(x_1, \cdots, x_m\right)= & c+c_1 x_1+\cdots+c_m x_m \\ & +c_{12} x_1 x_2+c_{13} x_1 x_3+\cdots \\ & +c_{m-1, m} x_{m-1} x_m+c_{123} x_1 x_2 x_3+\cdots \\ & +c_{12 \cdots m} x_1 x_2 \cdots x_m, \quad \end{aligned}\tag{1} \]

其中, 所有的系数 \(c_{i_1 \cdots i_l}\left(1 \leqslant i_1<i_2<\cdots<i_l \leqslant m, l\right.\) \(\geqslant 1)\) 和常数项 \(c\) 都属于 \(F_2\). 多项式 \(g\left(x_1, \cdots, x_m\right)\)对每个变量 \(x_i\) 的次数都不超过 \(1\) , 而 \(c_{i_1\cdots i_l}\) 的个数为 \(\{1,2, \cdots, m\}\) 的子集合的个数 \(2^m\). 换句话说, 在表达式 \((1)\) 的右边,形式上共有 \(2^m\) 个单项式 \(c_{i_1 \cdots i_l} x_{i_1} \cdots x_{i_l}\) (包括常数项). 当然在 \(c_{i_1 \cdots i_l}=0\) 时这个单项式在多项式 \(g\left(x_1, \cdots, x_n\right)\) 中并不出现.

定理 2 每个 \(m\) 元布尔函数 \(g(x_1, \cdots x_m)\) 均可唯一地表示成 \((1)\) 式的多项式形式.

证明：先证 \(g\left(x_1, \cdots, x_m\right)\) 必可表成 \((1)\) 的形式. 为此考虑如下的多项式:

\[h\left(x_1, \cdots, x_m\right) = \sum_{a=\left(a_1, \cdots, a_m\right) \in F_2^m} g\left(a_1, \cdots, a_m\right) \cdot\left(x_1+a_1+1\right) \cdots\left(x_m+a_m+1\right) \tag{2} \]

由于 \(g\left(a_1, \cdots, a_m\right) \in F_2\), 将右边展开再合并同类项, 可知 \(h\left(x_1, \cdots, x_m\right)\) 即为式 \((1)\) 右边的形式, 即对每个 \(x^i\) 的次数均 \(\leqslant 1\). 现在证明多项式 \(h\left(x_1, \cdots, x_m\right)\) 和 \(g\left(x_1, \cdots, x_m\right)\) 是同一个函数. 由于

\[x_i+a_i+1= \begin{cases}0, & x_i=a_i+1 \\ 1, & x_i=a_i,\end{cases} \]

可知

\[\begin{aligned} & \left(x_1+a_1+1\right) \cdots\left(x_m+a_m+1\right) = \begin{cases}1, & \left(x_1, \cdots, x_m\right)=\left(a_1, \cdots, a_m\right), \\ 0, & \text { 否则. }\end{cases} \end{aligned} \]

现在对每个 \(\left(b_1, \cdots, b_m\right) \in F_2^m\), 在 \((2)\) 式右边求和式中, 当代入 \(\left(x_1, \cdots, x_m\right)=\left(b_1, \cdots, b_m\right)\) 时,只剩下 \(\left(a_1, \cdots, a_m\right)=\left(b_1, \cdots, b_m\right)\) 的那一项不为零. 于是在 \(\left(x_1, \cdots, x_m\right)=\left(b_1, \cdots, b_m\right)\) 时, \((2)\) 式右边只剩下一项 \(g\left(b_1, \cdots, b_m\right)\). 这表明对每个 \(\left(b_1, \cdots, b_m\right)\), 多项式 \(h\left(x_1, \cdots, x_m\right)\) 和 \(g\left(x_1, \cdots, x_m\right)\) 的取值都一样. 所以每个 \(m\) 元布尔函数都可表示成像式 \((1)\) 那样的多项式形式. 由于这样的多项式有 \(2^{2^m}\) 个(它的 \(2^m\) 个系数 \(c_{i_1 \cdots i_i}\) 均可独立地为 \(0\) 或 \(1\)), 而 \(m\) 元布尔函数也有同样多个,所以形如式 \((1)\) 的不同多项式必为不同的布尔函数,这就证明了唯一性.

这个定理蕴含了这样一个事实————\(2^m\) 个单项式 \(x_{i_1} \cdots x_{i_l}\left(1 \leqslant i_1<i_2\right.\) \(\left.<\cdots<i_l \leqslant m, l \geqslant 0\right)\) 彼此之间是线性无关的。否则将会存在 \(m\) 元布尔函数 \(g\)，其多项式表达不唯一。

例 3 对于 \(m=3\), 设三元布尔函数 \(f\left(x_1, x_2, x_3\right)\) 在 \((000),(010),(111)\) 处取值为 \(1\),其他处取值为 \(0\) . 由式 \((2)\) 知求和式中在 \(f\) 取值为 \(0\) 的 \(\left(a_1, a_2, a_3\right)\) 不起作用,于是

\[\begin{aligned} f\left(x_1, x_2, x_3\right) = & \sum_{\substack{\left(a_1, a_2, a_3\right) \in F_2^3 \\ f(a_1, x_2, a_3)=1}}\left(x_1+a_1+1\right)\left(x_2+a_2+1\right)\left(x_3+a_3+1\right) \\ = & \left(x_1+1\right)\left(x_2+1\right)\left(x_3+1\right)+\left(x_1+1\right) x_2\left(x_3+1\right)+x_1 x_2 x_3 \\ = & 1+x_1+x_3+x_1 x_3+x_1 x_2 x_3 . \end{aligned} \]

今后以 \(B_m\) 表示全体 \(m\) 元布尔函数构成的集合. 由定理 \(2\) 可知这是 \(F_2\) 上的 \(2^m\) 维向量空间,其中, \(2^m\) 个单项式 \(x_{i_1} \cdots x_{i_l}\left(1 \leqslant i_1<i_2\right.\) \(\left.<\cdots<i_l \leqslant m, l \geqslant 0\right)\) 是向量空间 \(B_m\) 的一组基.
\(m\) 元布尔函数 \(f\) 的定义范围 \(F_2^m\) 是一个有限集合,可以把其中 \(2^m\) 个向量排定一个次序.通常按 \(0,1,2, \cdots, 2^m-1\) 的二进制展开

\[i=i_0+i_1 2+\cdots+i_{m-1} 2^{m-1}, \quad i_0, \cdots, i_{m-1} \in F_2 . \]

对应于向量 \(\left(i_0, i_1, \cdots, i_{m-1}\right) \in F_2^m\). 按此次序, \(F_2^m\)中全部向量排成:

\[\begin{array}{ll} v_0=(0,0, \cdots, 0), & v_1=(1,0, \cdots, 0), \\ v_2=(0,1,0, \cdots 0), & v_3=(1,1,0, \cdots, 0), \cdots, \\ v_{n-1}=(1,1, \cdots, 1), & n=2^m . \end{array} \]

然后便可把每个 \(m\) 元布尔函数 \(f\left(x_1, \cdots, x_m\right)\) 表示成 \(F_2^n\) 中的向量(也叫 \(f\) 的真值表或向量表示):

\[\boldsymbol{c_f}=\left(f\left(v_0\right), f\left(v_1\right), \cdots, f\left(v_{n-1}\right)\right) \in F_2^n, \quad n=2^m . \]

这时,布尔函数相加和相乘分别对应于向量按分量相加和相乘. 对于 \(f, g \in B_m\),

\[\begin{aligned} & \boldsymbol{c}_{f+g}=\left(f\left(v_0\right)+g\left(v_0\right), \cdots, f\left(v_{n-1}\right)+g\left(v_{n-1}\right)\right), \\ & \boldsymbol{c}_{f g}=\left(f\left(v_0\right) g\left(v_0\right), \cdots, f\left(v_{n-1}\right) g\left(v_{n-1}\right)\right) . \end{aligned} \]

例 4 对于 \(m=2, n=2^m=4\), 所以二元布尔函数共有 \(2^n=2^4=16\) 个. 它们的多项式表达式和向量表示如下表所示. 注意 \(B_2\) 是 \(F_2\) 上的 \(n\) \(=4\) 维向量空间, \(\left\{1, x_1, x_2, x_1 x_2\right\}\) 是 \(B_2\) 的一组基.

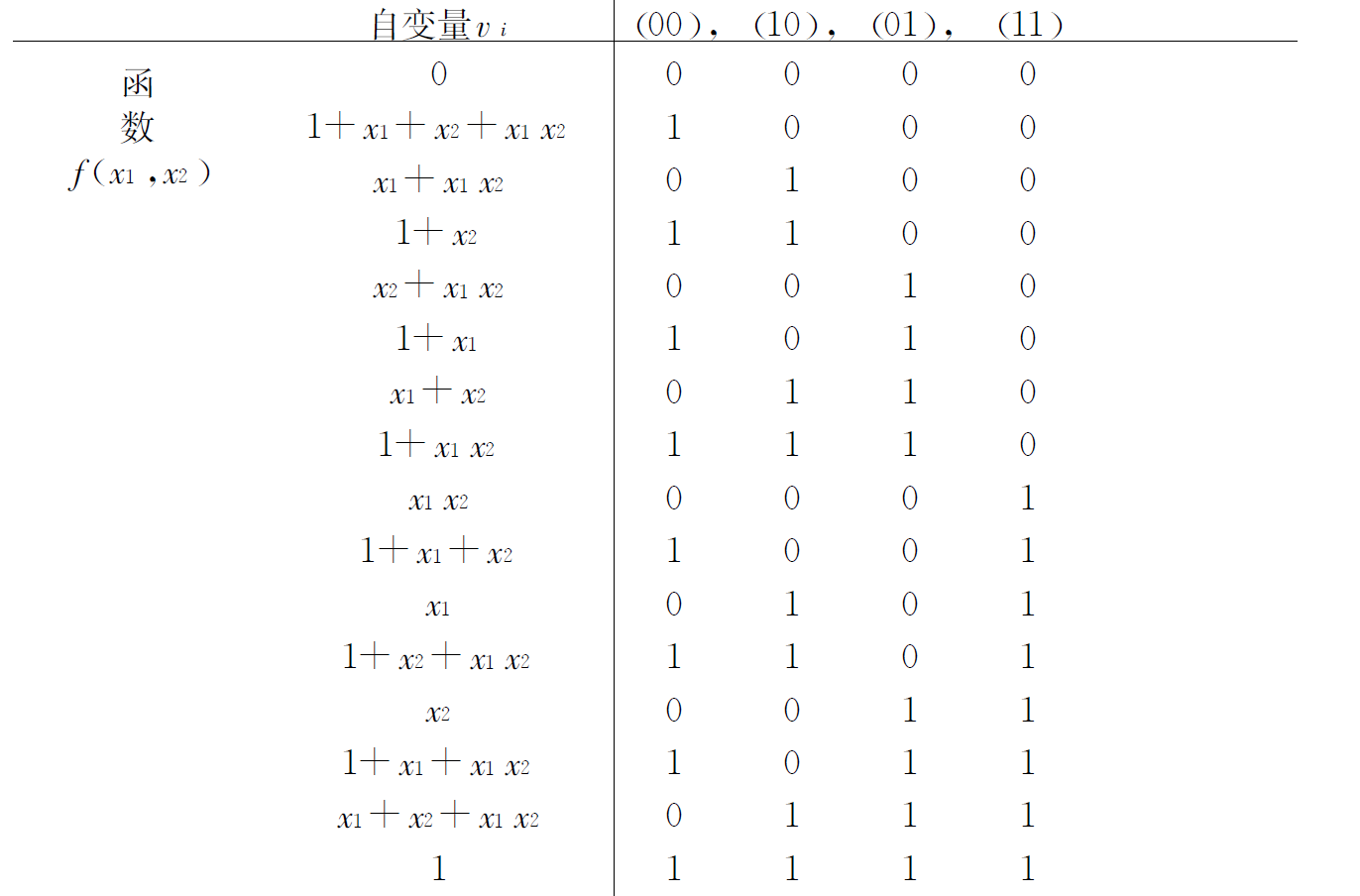
对于每个 \(m\) 元布尔函数 \(f=f\left(x_1, \cdots, x_m\right)\),向量 \(\boldsymbol{c}_f \in F_2^n\) 的汉明重量 \(w\left(c_f\right)\) 就是 \(f\) 在 \(F_2^n\) 上取值为 \(1\) 的自变量向量个数. 以下用 \(N_m(f=1)\) 和 \(N_m(f= 0 )\) 分别表示函数 \(f\) 取值为 \(1\) 和 \(0\) 的自变量向量个数,则

\[N_m(f=1)=w\left(c_f\right), \quad N_m(f=0)=2^n-w\left(c_f\right), n=2^m\]

引理 5 设 \(m \geqslant 1, f \in B_m, \operatorname{deg}(f)=r\) \((0 \leqslant r \leqslant m)\), 则 \(N_m(f=1) \geqslant 2^{m-r}\) 并且当 \(r \leqslant m-1\) 时, \(N_m(f=1)\) 为偶数.

先看看这个引理在说什么：当 \(r=m\) 时，\(N_m(f=1)\geq 1\) 当 \(f\) 是 \(m\) 次单项式时显然下界取到。如果不是 \(m\) 次单项式,用上表验证可知,也有像 \(1+x_1x_2\) 这样严格超过引理下界的情况。紧接着,引理断言,多项式次数每降低一次,\(N_m(f=1)\) 的下界就要 \(\times 2\)，这在直观上是可以理解的——要使 \(x_1x_2=1\) 需要 \(x_1\) 和 \(x_2\) 同时为 \(1\).但是想要使 \(x_1=1\) 仅需 \(x_1\) 为 \(1\)。满足后者的向量是前者的两倍。当然，引理处理的情形不是 \(m\) 次单项式而是多项式，复杂得多。对于引理的后半段,同样可以用单项式来验证和理解。

证明: 先证最后的论断. 对于每个次数 \(\leqslant\) \(m-1\) 的单项式 \(g=x_{i_1} \cdots x_{i_l}\left(1 \leqslant i_1<\cdots<i_l \leqslant m\right.\), \(l \leqslant m-1), g\) 取值为 \(1\) 当且仅当 \(x_{i_1}=\cdots=x_{i_i}=1\) 而其他 \(x_i\) 的值可以任取 \(0\) 或 \(1\) , 所以 \(N_m(g=\) \(1)=2^{m-l}\) 是偶数 (由于 \(l \leqslant m-1\) ), 即 \(c_g\) 的汉明重量为偶数. 每个次数 \(\leqslant m-1\) 的多项式 \(f \in B_m\) 都是这样一些单项式之和, 即 \(\boldsymbol{c}_f\) 都是汉明重量为偶数的 \(F_2^n\) 中一些向量之和, 所以 \(N_m(f=1)\) \(=w\left(c_f\right)\) 也是偶数.
现在对于 \(m\) 归纳证明引理 \(5\) 的前一论断, 即证明 \(f \in B_m, \operatorname{deg}(f)=r, 0 \leqslant r \leqslant m\) 时 \(N_m(f\) \(=1) \geqslant 2^{m-r}\). 对于 \(m=1\) 情形可以对 \(B_1\) 中 \(3\) 个一元非零布尔函数 \(1, x, x+1\) 直接验证. 现在设命题对 \(m-1\) 成立, \(m \geqslant 2\), 来证命题对 \(m\) 也成立.
当 \(r=0\) 时, \(f \equiv 1, N_m(f=1)=2^m\), 当 \(r=m\) 时, \(f \neq 0\), 从而 \(N_m(f=1) \geqslant 1=2^{m-r}\). 这表明命题在 \(r=0\) 和 \(m\) 时成立. 以下设 \(1 \leqslant r \leqslant m-1\). 可把 \(r\) 次 \(m\) 元布尔函数 \(f\left(x_1, \cdots, x_m\right)\) 唯一地写成

\[f=x_m h\left(x_1, \cdots, x_{m-1}\right)+g\left(x_1, \cdots, x_{m-1}\right), \]

其中, \(h, g \in B_{m-1}, \operatorname{deg}(h) \leqslant r-1, \operatorname{deg}(g) \leqslant r\). 如果 \(h \equiv 0\), 则
\(f=g\left(x_1, \cdots, x_{m-1}\right)\) 不依赖于 \(x_m\),

\[\begin{aligned} f\left(x_1, \cdots, x_{m-1}, 1\right) & =f\left(x_1, \cdots, x_{m-1}, 0\right) \\ & =g\left(x_1, \cdots, x_{m-1}\right) . \end{aligned} \]

所以

\[\begin{aligned} N_m(f=1) & =2 N_{m-1}(g=1) \\ & \geqslant 2 \cdot 2^{m-1-r} \text { (由归纳假设) } \\ & =2^{m-r} . \end{aligned} \]

如果 \(h \neq 0\), 则当 \(h\left(a_1, \cdots, a_{m-1}\right)=1\) 时,

\[f\left(a_1, \cdots, a_{m-1}, a_m\right)=a_m+g\left(a_1, \cdots, a_{m-1}\right) \text {. } \]

而当 \(h\left(a_1, \cdots, a_{m-1}\right)=0\) 时,

\[f\left(a_1, \cdots, a_{m-1}, a_m\right)=g\left(a_1, \cdots, a_{m-1}\right) . \]

每个使得 \(h=1\) 的向量 \(a\in F^{m-1}_2\) 都可以适当的调整 \(a_m\) 使得其对应一个使得 \(f=1\) 的向量 \(\hat a\in F^n_2\),因此

\[\begin{aligned} N_m(f=1) & \geqslant N_{m-1}(h=1) \\ & \geqslant 2^{(m-1)-(r-1)}(\text { 归纳假设 }) \\ & =2^{m-r} . \end{aligned} \]

这就归纳证明了引理 \(5\).

多元布尔函数是通信工程中的重要数学工具. 在信息安全方面,需要寻求一些布尔函数具有各种密码学的性质, 用来作为加密用的密钥,这是多年来的一个热门研究课题. 布尔函数看似简单, 但是当 \(m\) 较大时, \(m\) 元布尔函数的个数 \(2^n\left(n=2^m\right)\) 增加得很快, 所以要在其中选取对于某种性质最好的全部(甚至于一个)布尔函数都相当困难. 又如,为了对应于工程上用 “或门”和 “与门”的线路连接方式,布尔函数还可以表示成(不唯一的)逻辑表达式. 给定一个布尔函数，如何表示成逻辑表达式,使得所用逻辑运算个数最小(即实现这个布尔函数的逻辑线路中所需基本逻辑元件最少), 也是一个复杂而重要的实际问题. 诸如此类的关于布尔函数的问题, 需要用深人的数学工具 (如有限傅里叶变换)、设计实用算法的技巧和上机计算的能力. 本节介绍的布尔函数知识只是一些简单内容, 关于更多的知识可参见其他书籍.

最后,读者可能会问: 定义在二元域 \(F_2\) 上的布尔函数能否推广到任何有限域 \(F_p\) 上,一个 \(m\) 元 (广义)布尔函数 \(f: F_p^m \longrightarrow F_p\) 是否也都可以表示成 \(x_1, \cdots, x_m\) 的多项式 (系数属于 \(F_p\) )?
答案是肯定的, 留给读者作为习题.
但是若正整数 \(s \geqslant 4\) 不为素数,模 \(s\) 的同余类环 \(Z_s=\{0,1, \cdots, s-1\}\) 不是域, \(m\) 元函数 \(f=\) \(f\left(x_1, \cdots, x_m\right): Z_s^m \longrightarrow Z_s\) 不一定都能表成 \(x_{i_1}\cdots x_{i_l}\) 的多项式形式 (系数属于 \(Z_s\) ). 例如, 考虑最简单的情形

\[f=f(x): Z_4 \longrightarrow Z_4 . \]

由于对每个整数 \(a, a^4 \equiv a^2(\bmod 4)\), 所以 \(x^4\) 和 \(x^2\) 是 \(Z_4\) 上的同一个函数. 于是 \(Z_4\) 上每个多项式函数都可表示成 \(c_0+c_1 x+c_2 x^2+c_3 x^3\) 的形式, 其中 \(c_i \in Z_4\). 这样的表达式共 \(4^4\) 个, 但是 \(2 x^3\) 和 \(2 x\) 是同一个函数, 从而多项式函数少于 \(4^4\) 个. 而由 \(Z_4\) 到 \(Z_4\) 的函数共有 \(4^4\) 个, 这表明存在函数 \(f: Z_4 \longrightarrow Z_4\) 不能表示成多项式的形式.

定义 6 设 \(m \geqslant 1, n=2^m, 0 \leqslant r \leqslant m\). 向量空间 \(F_2^n\) 的子集合

\[\operatorname{RM}(r, m)=\{c_f=(f(\boldsymbol{v_0}), f(\boldsymbol{v_1}), \cdots,f(\boldsymbol{v}_{n-1})) \in F_2^n \mid f \in B_m, \operatorname{deg}(f) \leqslant r\}\]

叫做 \(r\) 阶的二元 \(Reed-Muller\) 码 (简称 \(RM\) 码). 这里向量 \(v_i=\left(i_0, i_1, \cdots, i_{m-1}\right) \in F_2^n\) 由 \(i\) 的 \(2\) 进制展开

\[i=i_0+i_1 2+\cdots+i_{m-1} 2^{m-1} ,0 \leqslant i \leqslant n-1=2^m-1 \]

给出.

定理 7
\((1)\) 二元 \(\mathrm{RM}\) 码 \(\mathrm{RM}(r, m)\) 是线性码, 基本参数为 \([n, k, d]=[2^m, k(m, r),2^{m-r}]\),其中,

\[k(m, r)=\sum_{t=0}^r\binom{m}{t}=1+\binom{m}{1}+\cdots+\binom{m}{r} . \]

\((2)\) 当 \(0 \leqslant r \leqslant m-1\) 时, \(\operatorname{RM}(r, m)\) 的对偶码 \(\mathrm{RM}(r, m)^{\perp}\) 为 \(\mathrm{RM}(m-r-1, m)\)

证明:
\((1)\) 当 \(f, g \in B_m\), 并且 \(\operatorname{deg}(f) \leqslant r\), \(\operatorname{deg}(g) \leqslant r\) 时, \(\operatorname{deg}(f+g) \leqslant \max (\operatorname{deg}(f), \operatorname{deg}(g)) \leqslant r\) 并且 \(\boldsymbol{c}_{f+g}=\boldsymbol{c}_f+\boldsymbol{c}_g\), 可知 \(\mathrm{RM}(r, m)\) 是线性码, 即若 \(\boldsymbol{c}, \boldsymbol{c}^{\prime} \in \mathrm{RM}(r, m)\), 则 \(\boldsymbol{c}+\boldsymbol{c}^{\prime} \in \mathrm{RM}\) \((r, m) . \mathrm{RM}(r, m)\) 的码长显然为 \(n=2^m\), 而所有次数 \(\leqslant r\) 的单项式 \(x_{i_1} \cdots x_{i_l}\left(1 \leqslant i_1<\cdots<i_l \leqslant m, l\right.\) \(\leqslant r)\) 的向量表示给出 \(\mathrm{RM}(r, m)\) 的一组基.

注意到布尔函数真值向量的线性无关性等价于布尔函数对应的多项式之间的线性无关性。

从而 \(\mathrm{RM}(r, m)\) 的维数就等于这样单项式的个数 \(k(r, m)=1+\binom{m}{1}+\cdots+\binom{m}{r}\). 最后决定 \(\mathrm{RM}(r,m)\) 的最小距离 \(d\). 根据引理 \(5\) , 对于 \(\mathrm{RM}(r,m)\) 中每个非零码字 \(\boldsymbol{c}_f\left(f \in B_m, 0 \leqslant \operatorname{deg}(f) \leqslant r\right)\), \(w\left(\boldsymbol{c}_f\right)=N_m(f=1) \geqslant 2^{m-r}\), 所以 \(d \geqslant 2^{m-r}\). 另一方面,对于布尔函数 \(f=x_1 \cdots x_r, w\left(\boldsymbol{c}_f\right)=N_m(f\) \(=1)=2^{m-r}\). 这就表明 \(d=2^{m-r}\).
\((2)\) \(\mathrm{RM}(r, m)\) 中码字为 \(\boldsymbol{c}_f\), 其中, \(f \in B_m\), \(\operatorname{deg}(f) \leqslant r, \operatorname{RM}(m-1-r, m)\) 中码字为 \(\boldsymbol{c}_g\), 其中 \(, g \in B_m, \operatorname{deg}(g) \leqslant m-1-r\). 于是 \(\operatorname{deg}(f g) \leqslant\) \(m-1-r+r=m-1\). 由引理 \(5\) 知 \(N_m(f g= 1)\)为偶数. \(F_2^n\) 中向量 \(\boldsymbol{c}_f\) 和 \(\boldsymbol{c}_g\) 的内积为

\(c_f\) 的长度为 \(2^m\),元素由 \(f\) 作用于全体 \(a\in F_2^m\) 给出。

\[\begin{aligned} \left(\boldsymbol{c}_f, \boldsymbol{c}_g\right) & =\sum_{a \in F_2^m} f(a) g(a)=\sum_{a \in F_2^m}(f g)(a) \\ & =N_m(f g=1)\equiv 0 \in F_2 . \end{aligned} \]

这表明 \(\mathrm{RM}(r, m)\) 中码字和 \(\mathrm{RM}(m-r-1, m)\)中码字均正交, 所以 $ \mathrm{RM}(m-r-1, m)\subseteq \mathrm{RM}(r, m)^{\perp}$. 考虑二者的维数,

\[\begin{aligned} & \operatorname{dim} \mathrm{RM}(r, m)+\operatorname{dim} \mathrm{RM}(m-r-1, m) \\ = & \sum_{t=0}^r\binom{m}{t}+\sum_{s=0}^{m-1-r}\binom{m}{s} \\ = & \sum_{t=0}^r\binom{m}{t}+\sum_{s=0}^{m-1-r}\binom{m}{m-s} \\ = & \sum_{t=0}^r\binom{m}{t}+\sum_{t=r+1}^m\binom{m}{t} \\ = & \sum_{t=0}^m\binom{m}{t}=2^m=n . \end{aligned} \]

因此 \(\operatorname{dim} \operatorname{RM}(r, m)^{\perp}=n-\operatorname{dim} \operatorname{RM}(r, m)=\) \(\operatorname{dim} \operatorname{RM}(m-r-1, m)\). 这就证明了 \(\mathrm{RM}(r, m)^{\perp}=\) \(\mathrm{RM}(m-r-1, m)\).

例 8 平凡的二元 \(\mathrm{RM}\) 码的例子是 \(\operatorname{RM}(0, m), \operatorname{RM}(m-1, m)\) 和 \(\operatorname{RM}(m, m)\). 由于次数 \(\leqslant 0\) 的 \(m\) 元布尔函数只有常值函数 \(0\) 和 \(1\) (像通常那样认为 \(\operatorname{deg}(0)=-\infty\)), 所以 \(\mathrm{RM}(0\), \(m)\) 由 \(F_2^n\) 中全 \(0\) 向量和全 \(1\) 向量两个码字组成,这和它的参数 \([n, k, d]=\left[2^m, 1,2^m\right]\) 是一致的.(同时也是平凡完全码)。 \(\mathrm{RM}(0, m)\) 的生成矩阵为 \((11 \cdots 1) \in F_2^n\), 它也是对偶码 \(\mathrm{RM}(0, m)^{\perp}=\mathrm{RM}(m-1, m)\) 的校验矩阵. 所以 \(\boldsymbol{a}=\left(a_0, \cdots, a_{n-1}\right) \in \operatorname{RM}(m-1, m)\) 当且仅当 \(a_0+a_1+\cdots+a_{n-1}=(11 \cdots 1) \boldsymbol{a}^{\mathrm{T}}=0\). 这就表明 \(\operatorname{RM}(m-1, m)\) 是 \(F_2^n\) 中所有汉明重量为偶数的向量组成的奇偶校验码 (例 \(1.1.1\)). 参数为 \([n, k, d]=\left[2^m, 2^m-1,2\right]\), 而 \(\operatorname{RM}(m, m)\) 是整个向量空间 \(F_2^n\),参数为 \(\left[2^m, 2^m, 1\right]\).

单项式(彼此线性无关且一起构成布尔函数空间的基)有 \(2^m\) 个，所有的布尔函数要多得多，有 \(2^{2^m}\) 个，其真值向量应两两不同故也有 \(2^{2^m}\) 个 \(\Rightarrow\) 布满了整个向量空间 \(F_2^n\).

例 9 一阶二元 \(\mathrm{RM}\) 码 \(\mathrm{RM}(1, m)\) 是由全体码字 \(c_f\) 组成,其中, \(f\) 是 \(m\) 元线性函数

\[f\left(x_1, \cdots, x_m\right)=b_1 x_1+\cdots+b_m x_m+b_0, b_i \in F_2 \tag{3} \]

由定理 \(7\) 知 \(\mathrm{RM}(1, m)\) 的参数为 \([n, k, d]=\) \(\left[2^m, 1+m, 2^{m-1}\right]\). 利用线性函数的表达式 \((3)\), 可以直接求出 \(\mathrm{RM}(1, m)\) 的最小距离 \(d=2^{m-1}\): 如果 \(b_1, \cdots, b_m, b_0\) 均为 \(0\) , 则 \(c_f\) 是零向量, 汉明重量为 \(0\) . 若 \(b_1, \cdots, b_m\) 不全为零, 则 \((3)\) 式中的 \(f \neq 0\). 而 \(w\left(\boldsymbol{c}_f\right)=N_m(f=1)\), 即 \(w\left(\boldsymbol{c}_f\right)\) 为线性方程

\[b_1 x_1+\cdots+b_m x_m+b_0=1 \]

在 \(F_2^m\) 中的解数. 当 \(b_1, \cdots, b_m\) 不全为零时, 解数为 \(2^{m-1}\). 这样码字个数(此时对 \(b_0\) 无要求)为 \(2(2^m-1)=2^{m+1}-2\),所以不仅得到 \(RM(1, m)\) 的最小距离为 \(2^{m-1}\), 而且还算出了它的重量多项式为

\[f_{\mathrm{RM}(1, m)}(z)=1+\left(2^{m+1}-2\right) z^{2^{m-1}}+z^{2^m} . \]

由于

\[\begin{aligned} \{\boldsymbol{c}_f= (f(v_0), f(v_1), \cdots, f(v_{n-1})) \mid f=1,x_1, x_2, \cdots, x_m\} \end{aligned} \]

是 \(\mathrm{RM}(1, m)\) 的一组基,(其中, \(v_i=(i_0, i_1, \cdots\), \(i_{m-1})\) 是由 \(i\) 的二进制展开 \(i=i_0+i_1 2+\cdots+\) \(i_{m-1} 2^{m-1}\left(i_0, \cdots, i_{m-1} \in F_2\right)\) 给出) 所以得到 \(RM(1, m)\) 的一个生成矩阵

\[\boldsymbol{G}=\left[\begin{array}{c} \boldsymbol{c}_1 \\ \boldsymbol{c}_{x_1} \\ \boldsymbol{c}_{x_2} \\ \boldsymbol{c}_{x_3} \\ \vdots \\ \boldsymbol{c}_{x_m} \end{array}\right]=\left[\begin{array}{ccccccc} 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 0 & 1 & 0 & 1 & 0 & \cdots & 1 \\ 0 & 0 & 1 & 1 & 0 & \cdots & 1 \\ 0 & 0 & 0 & 0 & 1 & \cdots & 1 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & 0 & \cdots & 1 \end{array}\right](最后一行前一半(2^{m-1}个)为 0，后一半为 1)\\ \]

\(=\left[\begin{array}{cccc} 1 & 1 & \cdots & 1 \\ 0 & & & \\ \vdots & & \boldsymbol{G}^{\prime} & \\ 0 & & & \end{array}\right], \quad n=2^m,\)

\(\mathrm{RM}(1, m)\) 中第 \(1\) 位为 \(0\) 的那些码字是由 \(\boldsymbol{G}\) 中除第 \(1\) 行之外的 \(m\) 行的线性组合,(由线性无关性)共有 \(2^m\) 个码字. 把它们第 \(1\) 位的零去掉, 所得的码是二元线性码, 叫做二元一阶线性码 \(\mathrm{RM}(1, m)\) 的收缩码, 表示成 \(\mathrm{RM}(1, m)^{\prime}\). 它有生成矩阵 \(\boldsymbol{G}^{\prime}\), 即为 \(\boldsymbol{G}\) 中除掉第 \(1\) 行和第 \(1\) 列的子阵 \(\boldsymbol{G}^{\prime}\).\(\mathrm{RM}(1, m)^{\prime}\) 的参数为 \(\left[2^m-1, m, 2^{m-1}\right]\).(删去一列相同的数字不会影响作为行的线性无关性以及最小距离) 由于

\[\operatorname{RM}(1, m)^{\prime}=\{(a_1, \cdots, a_{n-1}) \in F_2^{n-1} \mid(0, a_1, \cdots, a_{n-1}) \in \operatorname{RM}(1, m)\}, \]

而 \(\mathrm{RM}(1, m)\) 中非零和非全 1 码字的汉明重量均为 \(2^{m-1}\), 可知 \(\mathrm{RM}(1, m)^{\prime}\) 中非零码字也是如此. 所以 \(\operatorname{RM}(1, m)^{\prime}\) 的重量分布为

\[f_{\mathrm{RM}(1, m)^{\prime}}(z)=1+\left(2^m-1\right) z^{2^{m-1}} . \]

再注意到 \(\boldsymbol{G}^{\prime}\) 的第 \(i\) 列 \(\left(i_0, \cdots, i_{m-1}\right)^{\mathrm{T}}\) 恰好是 \(i\) 的二进展开 \(i=i_0+i_1 2+\cdots+i_{m-1} 2^{m-1}\) 的诸位数字, 而当 \(i\) 从 \(1\) 到 \(2^m-1(=n-1)\) 时 \(i\) 的二进展开给出的 \(\left(i_0, \cdots, i_{m-1}\right)\left(1 \leqslant i \leqslant 2^m-1\right)\) 恰好是 \(F_2^m\) 中所有 \(2^m-1\) 个非零向量, 所以 \(\boldsymbol{G}^{\prime}\) 中诸列恰好是 \(F_2^m\) 中全部 \(2^m-1\) 个非零向量, \(\boldsymbol{G}^{\prime}\) 正好是参数为 \(\left[2^m-1,2^m-1-m, 3\right]\) 的二元汉明码的校验矩阵！(见 \(2.2\) 节二元汉明码的定义.) 这就表明 \(\operatorname{RM}(1, m)^{\prime}\) 的对偶码是参数 \(\left[2^m-1,2^m-1\right.\) \(-m, 3]\) 的二元汉明码. 由于在汉明码的定义中, 所有长为 \(m\) 的非零向量排成校验矩阵的诸列时, 其次序可以是随意的, 所以更正确地说应该是:
定理 10 每个参数为 \(\left[2^m-1,2^m-1-\right.\) \(m, 3]\) 的二元汉明码 \(C_m\) 都等价于 \(\operatorname{RM}(1, m)^{\prime}\) 的对偶码.