七大排序——C实现

#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<time.h>
#define MAX_NUM_SIZE 20000000
#define MAX_RANDOM_NUM 100
#define SWAP(a,b){int temp; temp = a; a = b; b = temp;}

//冒泡排序
void bubbleSort(int a[]) {
    for (int x = 0; x < MAX_NUM_SIZE; x++) {
        for (int y = MAX_NUM_SIZE - 1; y >= x; y--) {
            if (a[x] > a[y]) {
                a[x] = a[x] + a[y];
                a[y] = a[x] - a[y];
                a[x] = a[x] - a[y];
            }
        }
    }
}

//选择排序
void selectSort(int a[]) {
    for (int i = 0; i < MAX_NUM_SIZE - 1; i++) {
        int min = i;        //min记录的是最小值的下标
        for (int j = i + 1; j < MAX_NUM_SIZE; j++) {
            if (a[min] > a[j]) {
                min = j;
            }
        }
        if (min != i) {
            SWAP(a[min],a[i]);
        }
    }
}

//插入排序
void insertSort(int a[]) {
    for (int i = 0; i < MAX_NUM_SIZE; i++) {
        int indexInsertedLast;
        int insertValue = a[i];
        for (indexInsertedLast = i - 1; indexInsertedLast >= 0 && a[indexInsertedLast] > insertValue;indexInsertedLast--) {
            a[indexInsertedLast + 1] = a[indexInsertedLast];
        }
        a[indexInsertedLast + 1] = insertValue;
    }
}

//希尔排序
void shellSort(int a[], int length) {
    for (int gap = length / 2; gap > 0; gap /= 2) {
        for (int i = gap; i < MAX_NUM_SIZE; i++) {
            int insertValue = a[i];
            int indexInsertedLast;
            for (indexInsertedLast = i - gap; indexInsertedLast >= 0 && a[indexInsertedLast] > insertValue; indexInsertedLast -= gap) {
                a[indexInsertedLast + gap] = a[indexInsertedLast];
            }
            a[indexInsertedLast + gap] = insertValue;
        }
    }
}

//快速排序
int partition(int *a, int left, int right) {
    int start, end;                                    //start是大于pivot的区间的开始位置的下标，end是该区间结束位置的下标
    for (start = left, end = left; end < right; end++) {//扩大小于pivot的数的区间
        if (a[end] < a[right]) {
            SWAP(a[start], a[end]);
            start++;
        }
    }
    SWAP(a[start], a[right]);                        //将pivot移到两个区间的交界处，分隔完成
    return start;                                    //返回pivot
}

void quickSort(int *a, int left, int right) {
    if (left < right) {                                //即元素个数至少为2
        int pivot = partition(a,left,right);
        quickSort(a, left, pivot - 1);
        quickSort(a, pivot + 1, right);
    }
}

//计数排序（多用于去除重复数字）
void countSort(int *a) {
    int count[MAX_RANDOM_NUM] = { 0 };                        //统计a中的元素出现次数到count中
    for (int i = 0; i < MAX_NUM_SIZE; i++) {
        count[ a[i] ] ++;
    }
    for (int index_count = 0, index_a = 0; index_count < MAX_RANDOM_NUM; index_count++) {
        for (int i = 0; i < count[index_count]; i++) {        //i是循环重复a中元素的次数
            a[index_a++] = index_count;                        //重复输出到a[]中
        }
    }
}

//堆排序（出现频率高）
void adjustMaxHeap(int *a, int originalFather, int lengthHeap) {
    int dad = originalFather;                    //当前的父节点
    int son = 2 * (originalFather + 1) - 1;        //当前的子节点
    while (son < lengthHeap) {                    //son < lengthHeap即子节点存在，子节点的下标范围在堆的大小以内
                                                //循环的效果是不断地执行循环，将左右子树比较，再将较大的子树与父比较，选出父与子树中最大的节点作最终的父节点
                                                //随着son++，会不断地向数的下方调整堆
        if (son + 1 < lengthHeap&&a[son] < a[son + 1]) {    //son+1为右子树的下标，这里是比较左右子树的大小，较大的将来要与父节点比较
            ++son;
        }
        if (a[son] > a[dad]) {                                //子树节点比父节点大，则交换子与父
            SWAP(a[son], a[dad]);
            dad = son;
            son = 2 * dad + 1;
        }
        else {
            break;                                            //子树节点比父节点小，则父节点位置稳定，结束这次调整堆
        }
    }
}

void heapSort(int *a) {
    //从最后一个父节点（MAX_NUM_SIZE / 2 - 1）开始，回头遍历父节点，初步调整堆
    for (int i = MAX_NUM_SIZE / 2 - 1; i >= 0; i--) {    //i为每个父节点的下标
        adjustMaxHeap(a, i, MAX_NUM_SIZE);
    }
    SWAP(a[0], a[MAX_NUM_SIZE - 1]);
    
    //初步调整完成后，不断将堆顶最大元素与堆的最后一个元素交换，再在下一次循环建堆时排除最后一个元素，以此缩小堆的规模
    for (int i = MAX_NUM_SIZE - 1; i > 1; i--) {    //i为堆的规模大小
        adjustMaxHeap(a, 0, i);
        SWAP(a[0], a[i - 1]);
    }
}



int compare(const void *pleft, const void *pright) {
    int *pa = (int *)pleft;
    int *pb = (int *)pright;
    return *pa - *pb;
}

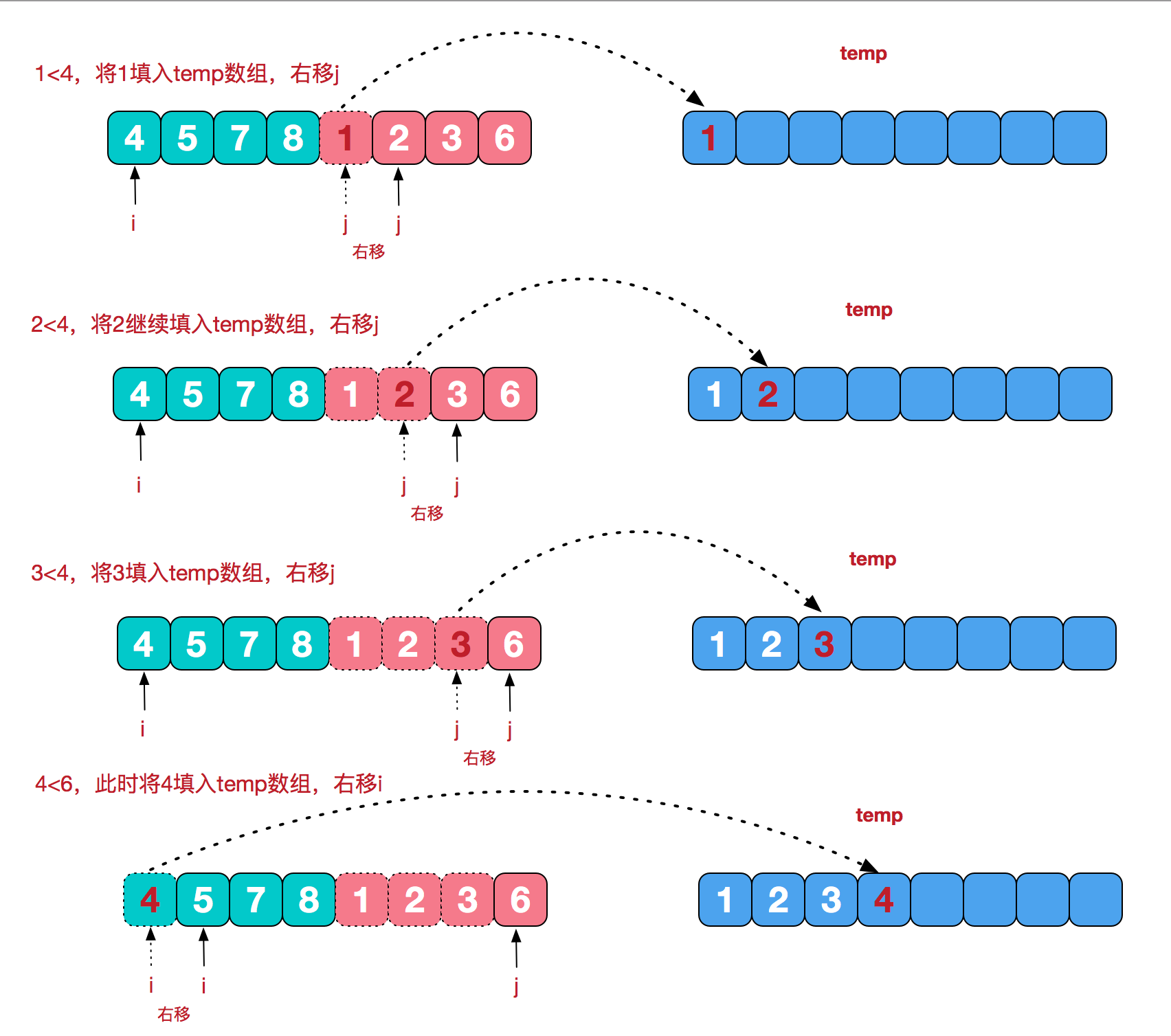
//归并排序
void merge(int *a, int left, int mid, int right) {
    int *b = (int *)malloc(MAX_NUM_SIZE * sizeof(int));
    memcpy(b, a, MAX_NUM_SIZE * sizeof(int));
    //leftPartP是左半边数组的当前下标，rightPartP是右半边的下标，destP是合并后的目标数组的当前下标
    int leftPartP = left, rightPartP = mid + 1, destinationP = left;
    while (leftPartP <= mid && rightPartP <= right) {
        if (b[leftPartP] < b[rightPartP]) {
            a[destinationP] = b[leftPartP];
            leftPartP++;
            destinationP++;
        }
        else {
            a[destinationP] = b[rightPartP];
            rightPartP++;
            destinationP++;
        }
    }
    while (leftPartP <= mid) {
        a[destinationP] = b[leftPartP];
        leftPartP++;
        destinationP++;
    }
    while (rightPartP <= right) {
        a[destinationP] = b[rightPartP];
        rightPartP++;
        destinationP++;
    }
    free(b);
    b = NULL;
}

void mergeSort(int *a, int left, int right) {
    if (left < right) {
        int mid = (left + right) / 2;    //mid是中间的下标
        mergeSort(a, left, mid);        //左半边归并排序
        mergeSort(a, mid + 1, right);    //右半边归并排序
        merge(a, left, mid, right);        //合并左右两边
    }
}

//快排的非递归的compare函数，原型类似于qsort(a, MAX_NUM_SIZE, sizeof(int), compare);
int compare(const void *pleft, const void *pright) {
    int *pa = (int *)pleft;
    int *pb = (int *)pright;
    return *pa - *pb;    //降序输出，如果要逆序输出就*pb - *pa
}

归并排序的图解，from——https://www.cnblogs.com/chengxiao/p/6194356.html