10 月 3 日模拟赛总结
Before
预期 \(100 + 100 + 100 + 0 = 300\)。
实际 \(30 + 10 + 100 + 0 = 140\)。
挂分 \(160\)。
rk23,菜。(简直了,跳的有多高就摔得有多惨)
T1
Description
给定 \(n\) 个 \(2\) 的幂 \(a_i\),相同数最多出现 \(2\) 次,令 \(k\) 为最大的幂次,求有多少种选数方案使得总和为 \(k + 1\) 次。
输入第一行一个整数 \(n\),随后第二行 \(n\) 个整数表示 \(a_i\)。
输出一行一个整数表示方案,对 \(998244353\) 取模。
\(1 \le n \le 10^5\),\(1 \le a_i \le 10^9\)。
Solution
其实很快就能找到规律:每次如果有连续的公差为 \(1\) 的上升序列,如果在 \(i\) 位置上的元素有两个,那么就相当于二进制进位,使得 \(\sum_{j=i}^n a_j=a^{k+1}\)。
可能这句话有点抽象,我们形象化一点:
给定一个数列 \(a=\{2,2,3,4\}\),则 \(k=4\),那么因为元素 \(2\) 有两个,所以把它们加起来就有了: \(2^2+2^2+2^3+2^4=4+4+8+16=32=2^{4+1}=2^5=32\)。
由此可以引申出结论:当 \(i\) 连续且公差为 \(1\) 时,有\(2^i \times 2+2^{i+1}+2^{i+2}+\cdots+2^{k}=2^{k+1}\),其中 \(i \le k\)。
因为每个数最多出现两次,那么我们只需要统计出现了两次的元素的个数并计算方案数即可。
考场想法:同上,但是写挂了。
考场寄因:写挂了。
时间复杂度 \(O(n \log n)\),空间复杂度 \(O(n)\)。
Code
\(\text{100pts:}\)
// 2023/10/3 _Pikachu_
#include <iostream>
#include <algorithm>
#include <map>
using namespace std;
typedef long long ll;
const int kMaxN = 1e5 + 7, mod = 998244353;
int n, m, a[kMaxN], ans;
map<int, int> mp;
int pow(int a, int b) {
ll res = 1;
while (b) {
if (b & 1) {
res = (res * a) % mod;
}
b >>= 1, a = (a * a % mod);
}
return res % mod;
}
int main() {
ios::sync_with_stdio(0), cin.tie(0);
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i], mp[a[i]]++;
}
sort(a + 1, a + 1 + n);
n = unique(a + 1, a + n + 1) - a - 1;
ans = (mp[a[n]] == 2);
for (int i = n - 1; i >= 1; i--) {
if (a[i] != a[i + 1] - 1) {
break;
}
ans += (mp[a[i]] == 2);
}
cout << pow(2, ans) - 1;
return 0;
}
\(\text{30pts:}\)
// 2023/10/3 _Pikachu_
#include <iostream>
#include <algorithm>
#include <map>
using namespace std;
typedef long long ll;
const int kMaxN = 1e5 + 7, mod = 998244353;
ll n, a[kMaxN], b[kMaxN], ans;
map<int, int> mp;
int main() {
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i];
mp[a[i]]++;
}
sort(a + 1, a + n + 1);
n = unique(a + 1, a + n + 1) - a - 1;
b[n + 1] = 1, b[n] = mp[a[n]];
for (int i = n - 1; i >= 1; i--) {
if (a[i] - a[i + 1] > 1) {
break;
}
b[i] = (b[i + 1] % mod * mp[a[i]] % mod) % mod;
}
for (int i = 1; i <= n; i++) {
if (mp[a[i]] == 2 && ((a[i] == (a[i + 1] - 1)) || (i == n))) {
ans = (ans % mod + b[i + 1] % mod) % mod;
}
}
cout << ans % mod << '\n';
return 0;
}
T2
Description
丛雨喜欢和朋友们玩一种桌游卡牌。这种卡牌共分四种颜色:红色、绿色、蓝色及黄色,每种颜色各有写着 \([0, 9]\) 的数字牌和功能牌:skip(跳牌)、reverse(反转出牌方向)。另有一些转色牌,不属于任何颜色。
游戏开始时,丛雨、芳乃、茉子每人从牌堆抽出 \(n\) 张牌,由丛雨第一个出牌,出牌顺序由丛雨决定。丛雨可以将任意牌作为第一张牌打出,接下来所有人出牌遵守以下规则:
按照丛雨规定的出牌顺序轮流出牌,必须出一张且只能出一张。若无符合规则的手牌可出,三人游戏失败。
若打出非转色牌,则所打出的牌要么颜色与上一张牌相同,要么数字与上一张牌相同(数字牌),要么功能与上一张牌相同(功能牌)。若为功能牌,执行对应功能:
skip:跳过下家出牌,由下家的下家打出下一张牌(由于只有 \(3\) 个人参加,下家的下家就是上家)。
reverse :将原本顺时针的出牌顺序变为逆时针,或相反,并由变化后的下家(原来的上家)打出下一张牌。
若打出转色牌,则无论上一张牌是什么都可以打出,且出牌者可决定下家应出哪种颜色的牌。
首先出完手牌的人胜出。而丛雨认为如果三个人能接连打出最后一张手牌,那么应该算共赢。
给出三人的手牌,请帮丛雨判断有没有共赢的可能性。
输入第一行一个整数 \(t\),表示数据组数。
对于每一组数据,第一行一个整数 \(n\),表示每人手里的手牌数。接下来 \(n\) 行,每一行 \(n\) 对整数,描述第 \(i\) 个人的第 \(j\) 张牌。用 \(0,1,2,3\) 表示红,黄,绿,蓝,若为 \(4\) 则为转色牌。第二个整数为数值或功能,\(10\) 表示 skip,\(11\) 表示 reverse。对于转色牌,第二个整数无效。
对于每一组数据,输出一个字符 Y 或 N,如果可以共赢输出 Y,否则输出 N。每一组数据用换行符隔开。
\(1 \le t \le 10\),\(1 \le n \le 6\)。
Solution
就是模拟。
我们可以使用 DFS,其中记录了是否胜利,当前出牌人,上一张牌的信息,和当前的出牌顺序。
然后我们用一个二维数组记录出牌顺序。
那么对于每一种情况我们暴力 check 就行了。
考场想法:暴力枚举每一种可能,\(O((n\times m)!)\) 这么大,我是怎么算的?
考场寄因:TLE。
时间复杂度 \(O(2^{3n})\),空间复杂度 \(O(n\times m)\),其中 \(m=3\)。
Code
\(\text{100pts:}\)
// 2023/10/3 _Pikachu_
#include <iostream>
#include <algorithm>
using namespace std;
const int kMaxN = 0x7F;
struct S {
int c, k;
} a[kMaxN][kMaxN];
int t, n;
bool b[kMaxN][kMaxN];
int cd[kMaxN], f[kMaxN][kMaxN];
bool DFS(int x, bool g, int lc, int lk, bool w) {
if (w && cd[x] > 1) {
return 0;
}
if (cd[x] == 0) {
return 1;
} else if (cd[x] == 1) {
w = 1;
}
for (int i = 1, c, k, nxt; i <= n; i++) {
c = a[x][i].c, k = a[x][i].k, nxt = f[g][x];
if (b[x][i]) {
continue;
}
if (lc == -1 || lc == 4 || c == lc || c == 4 || k == lk) {
b[x][i] = 1, cd[x]--;
if (cd[x] == 0) {
f[0][f[1][x]] = f[0][x];
f[1][f[0][x]] = f[1][x];
}
if (c == 4) {
if (DFS(nxt, g, c, k, w)) {
return 1;
}
} else if (k == 10) {
if (DFS(f[g][nxt], g, c, k, w)) {
return 1;
}
} else if (k == 11) {
if (DFS(f[!g][x], !g, c, k, w)) {
return 1;
}
} else {
if (DFS(nxt, g, c, k, w)) {
return 1;
}
}
b[x][i] = 0;
if (cd[x] == 0) {
f[0][f[1][x]] = x;
f[1][f[0][x]] = x;
}
cd[x]++;
}
}
return 0;
}
int main() {
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
for (cin >> t; t; t--) {
cin >> n;
for (int i = 0; i < 3; i++) {
for (int j = 1; j <= n; j++) {
cin >> a[i][j].c >> a[i][j].k;
b[i][j] = 0;
}
cd[i] = n, f[0][i] = (i + 2) % 3, f[1][i] = (i + 1) % 3;
}
if (DFS(0, 1, -1, -1, 0) || DFS(0, 0, -1, -1, 0)) {
cout << "Y\n";
} else {
cout << "N\n";
}
}
return 0;
}
\(\text{10pts:}\)
// 2023/10/3 _Pikachu_
#include <iostream>
#include <algorithm>
using namespace std;
const int kMaxN = 0x7F;
struct S {
int c, k;
} a[kMaxN];
int t, n, m = 3, x[kMaxN], y[kMaxN], z[kMaxN], f[kMaxN], b[kMaxN] = {0, 1, 2, 3}, len;
int c[kMaxN];
int main() {
freopen("uno.in", "r", stdin);
freopen("uno.out", "w", stdout);
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
for (cin >> t; t; t--) {
cin >> n;
for (int i = 1; i <= n; i++) {
x[i] = i;
y[i] = i + n;
z[i] = i + n * 2;
}
for (int i = 1; i <= 3; i++) {
b[i] = i;
}
for (int i = 1; i <= m; i++) {
for (int j = 1, c, k; j <= n; j++) {
cin >> c >> k;
a[++len] = (Shit){c, k};
}
}
bool sol = 1;
do {
do {
do {
do {
sol = 1;
for (int i = 1; i <= m; i++) {
c[i] = b[i];
}
for (int i = 0, p = 0; i < len; i++) {
if (c[i % 3 + 1] == 1) {
f[++p] = x[i / 3 + 1];
} else if (c[i % 3 + 1] == 2) {
f[++p] = y[i / 3 + 1];
} else {
f[++p] = z[i / 3 + 1];
}
}
for (int i = 2, q = 0, h = 1; i <= len; i++) {
if (q == 1) {
q--;
continue;
}
if (a[f[i]].c != 4) {
if (a[f[i - h]].c == a[f[i]].c) {
h = 1;
continue;
} else if (a[f[i - h]].k == a[f[i]].k) {
h = 1;
if (a[f[i]].k == 10) {
q = 1, h = 2;
continue;
} else if (a[f[i]].k == 11) {
reverse(c + 1, c + m + 1);
continue;
} else {
continue;
}
} else {
sol = 0;
break;
}
} else {
h = 2;
if (i == n || i == n - 1) {
break;
} else {
a[f[i + 1]].c = a[f[i + 2]].c;
}
}
}
if (sol) {
break;
}
} while (next_permutation(z + 1, z + n + 1));
if (sol) {
break;
}
} while (next_permutation(y + 1, y + n + 1));
if (sol) {
break;
}
} while (next_permutation(x + 1, x + n + 1));
if (sol) {
break;
}
} while (next_permutation(b + 2, b + m + 1));
cout << (sol ? "Y" : "N") << '\n';
len = 0;
}
return 0;
}
T3
Description
给定一组四个整数 \(a_i\) 和一组三个整数 \(b_i\),求每组各选一个整数的最小总和。
输入第一行四个整数,第二行三个整数。
输出一行一个答案。
\(1 \le a_i \le 1000\),\(1 \le b_i \le 1000\)。
Solution
毫无难度,应该都会做吧?
考场想法:模拟。
考场寄因:没寄。
时间复杂度 \(O(n)\),空间复杂度 \(O(n)\),其中 \(n=4\)。
Code
\(\text{100pts:}\)
// 2023/10/3 _Pikachu_
#include <iostream>
using namespace std;
const int kMaxN = 11;
int n = 4, m = 3, a[kMaxN], b[kMaxN], min1 = 1919810, min2 = 1919810;
int main() {
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
for (int i = 1; i <= n; i++) {
cin >> a[i];
min1 = min(min1, a[i]);
}
for (int i = 1; i <= m; i++) {
cin >> b[i];
min2 = min(min2, b[i]);
}
cout << min1 + min2 << '\n';
return 0;
}
T4
Description
给定一个平面点集,求有多少子集满足,按照 \(y\) 降序排序后,对每个 \(j\) 都满足 \(x_{j - 2} < x_j < x_{j - 1}\) 或者 \(x_{j - 1} < x_j < x_{j - 2}\) 。
输入一行一个整数 \(n\),接下来 \(n\) 对整数描述一个点的坐标。
输出一行一个答案对 \(10^9 + 7\) 取模的结果。
\(1 \le n \le 6000\),\(0 \le | x_i | \le 10^9\),\(0 \le | y_i | \le 10^9\),\(x_i\) 互不相同,\(y_i\) 互不相同。
Solution
要使得其符合上述写到的条件,那么点集排列的形状一定是这样的:
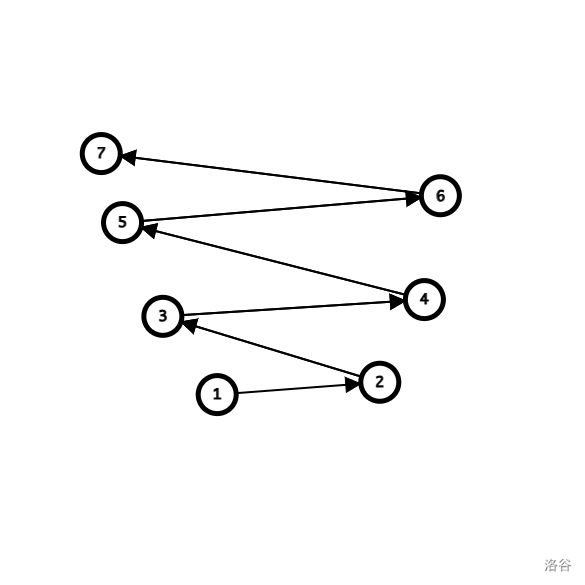
也就是说,我们以 \(x\) 为关键字排序,从后往前选择点,\(y\) 一定单调递增。
我们可以把点集分为两个点集,一个相对左,一个相对右。
考虑转移:
-
如果要从右边的点转移到左边的点,一定满足 \(y_i<y_j\)。
-
如果要从左边的点转移到右边的点,一定满足 \(y_i>y_j\)。
转移条件有了,接下来我们推方程:
设 \(f_i\) 为从右向左转移的第 \(i\) 点的方案数, \(g_i\) 为从左向右转移的第 \(i\) 点的方案数。
那么我们固定右边的 \(i\) 点,然后从上往下向下方的点转移:
-
对于 \(f_j\),也就是小于 \(i\) 的每个点,我们的方案数可以从右边转移过来,即加上右边的方案数。
-
如果左边转移完了,那么就要将左边所有的方案数全部转移到第一个 \(y_i>y_j\) 的点。
然后将对于每个点的方案数加起来即可,但是对于每个点都会多计算一次,所以最后的答案需要减一。
考场想法:没写。
考场寄因:没写。
时间复杂度 \(O(n^2)\),空间复杂度 \(O(n)\)。
Code
\(\text{100pts:}\)
// 2023/10/3 _Pikachu_
#include <iostream>
#include <algorithm>
using namespace std;
const int kMaxN = 6007, mod = 1e9 + 7;
struct P {
int x, y;
bool operator < (const P &p) const {
return x < p.x;
}
} a[kMaxN];
int n, f[kMaxN], g[kMaxN], ans;
int main() {
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i].x >> a[i].y;
}
sort(a + 1, a + n + 1);
for (int i = 1; i <= n; i++) {
f[i] = g[i] = 1;
for (int j = i - 1; j; j--) {
if (a[i].y < a[j].y) {
f[j] = (f[j] + g[i]) % mod;
} else {
g[i] = (g[i] + f[j]) % mod;
}
}
}
for (int i = 1; i <= n; i++) {
ans = (ans + f[i]) % mod;
ans = (ans + g[i]) % mod;
}
cout << (ans - n) % mod;
return 0;
}
Summary
需要掌握的:码力。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号