浅谈LCA问题（最近公共祖先）（四种做法）

【模板】最近公共祖先（LCA）

\(update \ 2023.1.3\) 新增了树链剖分

题目描述

如题，给定一棵有根多叉树，请求出指定两个点直接最近的公共祖先。

输入格式

第一行包含三个正整数 \(N,M,S\)，分别表示树的结点个数、询问的个数和树根结点的序号。

接下来 \(N-1\) 行每行包含两个正整数 \(x, y\)，表示 \(x\) 结点和 \(y\) 结点之间有一条直接连接的边（数据保证可以构成树）。

接下来 \(M\) 行每行包含两个正整数 \(a, b\)，表示询问 \(a\) 结点和 \(b\) 结点的最近公共祖先。

输出格式

输出包含 \(M\) 行，每行包含一个正整数，依次为每一个询问的结果。

样例 #1

样例输入 #1

样例输出 #1

提示

对于 \(30\%\) 的数据，\(N\leq 10\)，\(M\leq 10\)。

对于 \(70\%\) 的数据，\(N\leq 10000\)，\(M\leq 10000\)。

对于 \(100\%\) 的数据，\(N\leq 500000\)，\(M\leq 500000\)。

样例说明：

该树结构如下：

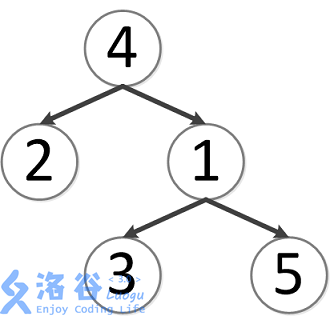
第一次询问：\(2, 4\) 的最近公共祖先，故为 \(4\)。

第二次询问：\(3, 2\) 的最近公共祖先，故为 \(4\)。

第三次询问：\(3, 5\) 的最近公共祖先，故为 \(1\)。

第四次询问：\(1, 2\) 的最近公共祖先，故为 \(4\)。

第五次询问：\(4, 5\) 的最近公共祖先，故为 \(4\)。

故输出依次为 \(4, 4, 1, 4, 4\)。

2021/10/4 数据更新 @fstqwq：应要求加了两组数据卡掉了暴力跳。

浅浅分析一下？

首先，知道最近公共祖先是什么意思
这个节点的父节点，父节点的父节点都是祖先……，甚至自己都是祖先
去看看这个题的样例解释，明白了这个概念后，再看后面。

暴力做法？

不要把算法想的太复杂，说到底，就是暴力的思路，然后想尽办法优化，什么常数优化啊一大堆乱七八糟的。
这道题也是一样，我们来考虑暴力做法
记录一个点的所有祖先，枚举另一个点的祖先，相同输出。
如果出题人故意卡你，给你出一个两条互不相同的链，然后头结点拼起来，然后给你一个查询：两条链的尾结点，你肯定会超时。

倍增

预处理
我们需要知道每个点的祖先，但不需要全部，毕竟空间存不下（具体思路见我RMQ的思路）
\(f[i][j]\)表示\(i\)的\(2^j\)级祖先是谁
\(f[i][0]\)表示\(i\)的父亲…………
状态转移方程:\(f[i][j]=f[f[i][j-1]][j-1]\)
这个怎么记呢？
“爸爸的爸爸叫爷爷”
查询
第一步：对齐
若\(x，y\)深度不一样,不妨设\(x\)的深度\(>y\)的深度
首先令\(x\)爬到\(x\)的某个深度与\(y\)相等的祖先
如果\(y==x\)那\(y\)就是\(x\)的祖先，输出\(y\)即可，否则进入下一步
第二步：爬树
\(x,y\)以倍增的形式向上爬树，单次查询:\(O({log_{2}}^{n})\)
\(dfs\)查询每个节点的\(2^j\)级祖先（这里用的是链式前向星存储）（~~不会的去查吧~~）

void dfs(int x,int fat)
{
	fa[x][0]=fat;
	deep[x]=deep[fat]+1;//深度等于他爸的深度+1
	for(int i=1;i<=lg[deep[x]];++i)
		fa[x][i]=fa[fa[x][i-1]][i-1];//爸爸的爸爸叫爷爷
	for(int i=head[x];i;i=edge[i].next)
		if(edge[i].to!=fat)//不是父亲
			dfs(edge[i].to,x);//遍历
	}

开始爬树（同一高度）

int LCA(int x,int y)
{
	if(deep[x]<deep[y])
		swap(x,y);//不妨设x深度大于y
		while(deep[x]>deep[y])
			x=fa[x][lg[deep[x]-deep[y]]-1];//RMQ讲过的，log值要减一
	if(x==y)return x;//y是x的祖先
//现在x和y在同一深度上

继续爬树

for(int k=lg[deep[x]]-1;k>=0;k--)//注意遍历顺序
		if(fa[x][k]!=fa[y][k]){//没爬到
			x=fa[x][k];      
			y=fa[y][k];      			
		}
		//也许超了，不往上爬                      
	return fa[x][0];//爬完之后，它肯定在最近公共祖先的儿子，返回他爸                   
	}

\(Code:\)

#include<bits/stdc++.h>

using namespace std;
struct node{int to,nxt;}edge[1000005];
int n,m,s,head[1000005],cnt;
int fa[1000005][25],r[1000005],lg[1000005];
void log_2(int k){
	for(int i=1;i<=k;i++)
		lg[i]=lg[i-1]+((1<<lg[i-1])==i);
}
void add(int from,int to){
	edge[++cnt].to=to,edge[cnt].nxt=head[from],head[from]=cnt;
}
void dfs(int u,int fat){//dfs初始化fa数组
	fa[u][0]=fat,r[u]=r[fat]+1;
	for(int i=1;i<lg[r[u]];/*注意-1*/i++) 
		fa[u][i]=fa[fa[u][i-1]][i-1];//爸爸的爸爸叫爷爷
	for(int i=head[u];i;i=edge[i].nxt)
		if(edge[i].to!=fat)
			dfs(edge[i].to,u);
}
int LCA(int x,int y){
	if(r[x]<r[y])swap(x,y);//不妨设x比y深 
	while(r[x]>r[y])
		x=fa[x][lg[r[x]-r[y]]-1];//注意减一 
	if(x==y) return y;//y是x的祖先
	for(int i=lg[r[x]]-1;i>=0;i--){//预好跳完整个数的准备，从大到小，注意减一 
		if(fa[x][i]!=fa[y][i]) x=fa[x][i],y=fa[y][i];//跳
		//不然什么都不干 
	}
	return fa[x][0];//返回他的父亲，自行模拟 
}
int main()
{
	cin>>n>>m>>s;
	for(int i=1;i<n;i++){
		int u,v;scanf("%d %d",&u,&v);
		add(u,v),add(v,u);
	}
	log_2(n);
	dfs(s,0);
	for(int i=1;i<=m;i++){
		int x,y;scanf("%d %d",&x,&y);
		printf("%d\n",LCA(x,y));
	}
	return 0;
}

RMQ

这东西没想出来正常（~~因为我没有想出来~~），非常神奇
我们先来了解各个需要用到的数组含义
\(ver[i]\)表示\(dfs\)第\(i\)个访问的节点
\(R[i]\)表示\(ver[i]\)所在的层数，也就是深度
\(first[i]\)表示\(i\)个节点在\(ver[i]\)的最小编号，也就是第一个出现的编号
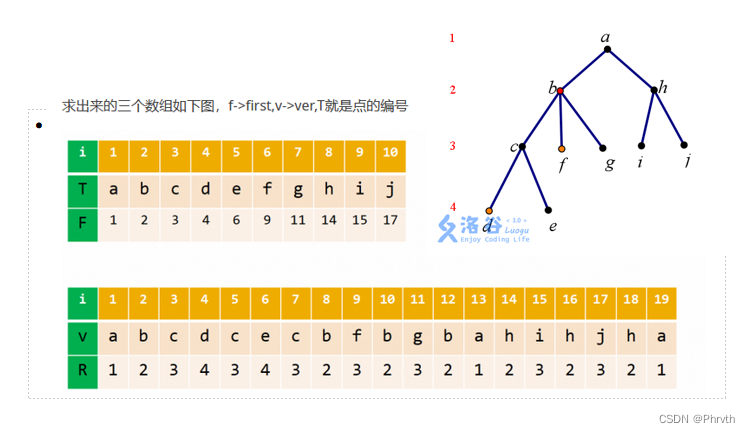
如果我们要求\(d\)和\(f\)的\(LCA\)，我们发现\(d\)第一次出现在\(4\)，\(f\)第一次出现在\(9\)，由\(dfs\)的性质可以知道，在\(4~9\)之间深度最小的点就是\(LCA\)
这不就是区间查询问题吗？
于是我们就想到了\(RMQ\),预处理\(O(n{log_{2}}^n)\),查询:\(O(1)\)非常之快
直接上代码，都讲过（~~三个数组的预处理都会吧~~）
\(Code:\)

//LCA（RMQ方法） 
#include<bits/stdc++.h>

using namespace std;
struct node{int value,nxt,to;}edge[2000005];
int n,m,s,head[1000005],cnt,tot;
int fir[1000005];//每个点第一次出现的时间 
int ver[1000005];//时间戳
int r[1000005];//时间戳每个点的深度 
int f[20][1000005];//RMQ数组（记录深度）
int rec[20][1000005];//记录标号 
int lg[1000005];//log2数组 
void tiao_shi(){
	for(int i=1;i<=tot;i++) cout<<ver[i]<<' ';
	cout<<endl;
	for(int i=1;i<=tot;i++) cout<<r[i]<<' ';
	cout<<endl;
	for(int i=1;i<=n;i++) cout<<fir[i]<<' ';
	cout<<endl;
}
void add(int from,int to){//链式前向星 
	edge[++cnt].to=to,edge[cnt].nxt=head[from],head[from]=cnt;
}
void log_2(int k){
	for(int i=1;i<=k;i++)
		lg[i]=lg[i-1]+(1<<lg[i-1]==i);
}
void dfs(int u,int dep){
	fir[u]=++tot,ver[tot]=u,r[tot]=dep;
	for(int i=head[u];i;i=edge[i].nxt){
		int v=edge[i].to;
		if(!fir[v])
			dfs(v,dep+1),ver[++tot]=u,r[tot]=dep;//去了又,回来 
	}
}
void RMQ_init(){//RMQ初始化,详见RMP模板 
	log_2(tot);//求log2 1~tot比cmath库的函数快很多
	for(int i=1;i<lg[tot];i++)
		for(int j=1;j+(1<<i)-1<=tot;j++)
			f[i][j]=1e9; 
	for(int i=1;i<=tot;i++)//数组初始化 
		f[0][i]=r[i],rec[0][i]=ver[i];
	for(int i=1;i<lg[tot];i++)
		for(int j=1;j+(1<<i)-1<=tot;j++){
			if(f[i-1][j]<f[i-1][j+(1<<i-1)])
				f[i][j]=f[i-1][j],rec[i][j]=rec[i-1][j];
			else f[i][j]=f[i-1][j+(1<<i-1)],rec[i][j]=rec[i-1][j+(1<<i-1)];//聚合 
		}
}
int main()
{
	cin>>n>>m>>s;
	for(int i=1;i<n;i++){
		int u,v;scanf("%d %d",&u,&v);
		add(u,v),add(v,u);
	}
	dfs(s,1);
	RMQ_init();
	for(int i=1;i<=m;i++){
		int l,r;scanf("%d %d",&l,&r);
		l=fir[l],r=fir[r];
		if(l>r)swap(l,r);
		int k=lg[r-l+1]-1;//注意减一  
		if(f[k][l]<f[k][r-(1<<k)+1]) printf("%d\n",rec[k][l]);
		else printf("%d\n",rec[k][r-(1<<k)+1]);
	}
	//详细见RMQ,这里只提供思路 
//	tiao_shi();
	return 0;	
}

tarjan

自认为讲不清楚
推荐一个详解博客：tarjan——LCA
这里说一下简略思路
第一步遍历，\(DFS\)遍历，如果走不下去了，就把那个点用并查集并起来
然后用一个\(vis\)数组标记，如果遍历到一个点，寻找和他有关系的点，如果那个点被标记过了，他们的最近公共祖先就是\(find(那个点)\)
详细请见那个博客，这里给出这个博客给的思路写出来的代码
\(Code:\)

#include<bits/stdc++.h>

using namespace std;
struct node{int to,nxt,id;}edge[1000005],deg[1000005];
int n,m,s,cnt,dcnt,head[1000005],dhd[1000005],ict;
int fa[1000005],rak[1000005];//并查集
int vis[1000005];//标记数组 
int ans[1000005];//答案数组 
void add(int from,int to){
	edge[++cnt].to=to,edge[cnt].nxt=head[from],head[from]=cnt;
}
void dadd(int from,int to){
	deg[++dcnt].to=to,deg[dcnt].nxt=dhd[from],dhd[from]=dcnt,deg[dcnt].id=++ict;
	deg[++dcnt].to=from,deg[dcnt].nxt=dhd[to],dhd[to]=dcnt,deg[dcnt].id=ict;
}
void init(){
	for(int i=1;i<=n;i++) fa[i]=i;
}
int find(int x){
	if(x==fa[x]) return x;
	return fa[x]=find(fa[x]);//小优化 
}
void marge(int u,int v){//不能用按秩合并，有顺序的限定！ 
	int f1=find(u),f2=find(v);
	fa[f2]=f1;
}
void tarjan(int u,int fat){
	vis[u]=1;
	for(int i=head[u];i;i=edge[i].nxt)
		if(!vis[edge[i].to]&&edge[i].to!=fat)//并查集挺高查找速度 
			tarjan(edge[i].to,u),marge(u,edge[i].to);
	for(int i=dhd[u];i;i=deg[i].nxt)
		if(vis[deg[i].to]&&!ans[deg[i].id])
			ans[deg[i].id]=find(deg[i].to);
}
int main()
{
	cin>>n>>m>>s;
	for(int i=1;i<n;i++){
		int u,v;cin>>u>>v;
		add(u,v),add(v,u);
	}
	for(int i=1;i<=m;i++){
		 int x,y;cin>>x>>y;
		 dadd(x,y);
	}
	init();
	tarjan(s,0);
	for(int i=1;i<=ict;i++) cout<<ans[i]<<endl;
	return 0;
}

树链剖分

个人认为树剖是倍增的另一种优化形式
倍增是使用\(ST\)表这一神奇东西优化
而树剖就是将一棵树分成若干条链，进而减少跳树的过程
而怎么将一棵树分成几条链呢？
先看看下面一些元素的定义

重儿子：指的是以这棵树的儿子为根的子树元素最多的儿子
不理解？
看看这张图

节点\(1\)有\(2\)个儿子，分别是节点\(2\)和节点\(3\),以\(2\)根的子树的元素数量为\(1\)(就他自己)（为了方便，以\(x\)为分根的子树的元素数量为\(size_x\)）
而\(size_3=2\)，所以元素\(1\)的重儿子是\(3\)

2.有重儿子自然也有轻儿子，轻儿子就是父节点除了重儿子以外的儿子，很好理解吧
3.重边：父节点与重儿子的连线
4.轻边：父节点与轻儿子的连线
5.重链：多条重边组成的链
6.轻链：多条轻边组成的链
来自一篇博客
比如上面的图，黑色粗边组成的链子就是重链，其他是轻链
注意：标有红色点的是每条重链的起点

好啦，以上就是一些基础元素，如果你学到这里全部理解，那么下面的实现肯定难不倒你捏
回到正题，首先我们肯定要建链（~~不准确学名~~），我们首先先把整个树建出来并且把每个点的重儿子找出来

int f[MAXN], d[MAXN], son[MAXN], size[MAXN];
//f[i]是i的父亲
//d[i]是i的深度
//son[i]是i的重儿子
//size[i]是以i为根的子树的元素总和
void dfs1(int u, int fa, int depth) {//u：现在的点，fa：字面意思，depth：字面意思
	f[u] = fa, d[u] = depth, size[u] = 1;//附初值
	for (int i = head[u]; i; i = edge[i].nxt) {
		int v = edge[i].to;
		if(f[u] == v) continue;
		dfs1(v, u, depth + 1);
		size[u] += size[v];//要先递归，此时size[v]是求出来的
		if(size[v] > size[son[u]]) son[u] = v;//求重儿子
	}
}

接下来，我们就可以正儿八经的建链啦

int top[MAXN], id[MAXN], rt[MAXN], l_cnt;
//top[i]表示i所在的链的链头，即上文图片中打红色点的节点
//id[i],rt[i],l_cnt求和用的，这里先不讲
void dfs2(int u, int t) {
	top[u] = t, id[u] = ++l_cnt, rt[l_cnt] = u;
	if(!son[u]) return ;//叶子节点return掉
	dfs2(son[u], t);//要想清楚，一条重链的节点都是重儿子，所以这条链的top还是原来的top
	for (int i = head[u]; i; i = edge[i].nxt) {
		int v = edge[i].to;
		if(v != son[u] && v != f[u]) //处理轻儿子
			dfs2(v, v);//轻儿子的链头是自己啦
	} 
}

建完链之后我们就可以求\(LCA\)啦
具体做法就是让两个点条到一条链上，然后高的那个点（也有可能一样高）就是公共祖先啦

int LCA(int x, int y) {
	while(top[x] != top[y]) {
		if(d[top[x]] < d[top[y]]) swap(x, y);//不妨设d[x]大于d[y]
		x = f[top[x]];//跳到链头的父亲那，也就是比他高一级的链的末尾
	}
	if(d[x] > d[y]) swap(x, y);
	return x;//高的那个点就是公共祖先
}

这道题到这里就结束了，配上~~高清无码~~代码

\(\mathcal{Code}\)

#include<bits/stdc++.h>

using namespace std;
const int MAXN = 5e5 + 7;

struct node{int nxt, to;}edge[2 * MAXN];
int cnt, head[MAXN];
inline void add(int front, int to) {edge[++cnt].to = to, edge[cnt].nxt = head[front], head[front] = cnt;}

int f[MAXN], d[MAXN], son[MAXN], size[MAXN];
void dfs1(int u, int fa, int depth) {
	f[u] = fa, d[u] = depth, size[u] = 1;
	for (int i = head[u]; i; i = edge[i].nxt) {
		int v = edge[i].to;
		if(f[u] == v) continue;
		dfs1(v, u, depth + 1);
		size[u] += size[v];
		if(size[v] > size[son[u]]) son[u] = v;
	}
}
int top[MAXN], id[MAXN], rt[MAXN], l_cnt;
void dfs2(int u, int t) {
	top[u] = t, id[u] = ++l_cnt, rt[l_cnt] = u;
	if(!son[u]) return ;
	dfs2(son[u], t);
	for (int i = head[u]; i; i = edge[i].nxt) {
		int v = edge[i].to;
		if(v != son[u] && v != f[u]) 
			dfs2(v, v);
	} 
}
int LCA(int x, int y) {
	while(top[x] != top[y]) {
		if(d[top[x]] < d[top[y]]) swap(x, y);
		x = f[top[x]];
	}
	if(d[x] > d[y]) swap(x, y);
	return x;
}
 
int N, M, S, x, y, a, b;

int main() {
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	
	cin >> N >> M >> S;
	for (int i = 1; i < N; i++) {
		cin >> x >> y;
		add(x, y), add(y, x);
	}
	
	dfs1(S, 0, 1);
	dfs2(S, S);
	for (int i = 1; i <= M; i++) {
		cin >> a >> b;
		cout << LCA(a, b) << endl;
	}
	return 0;
}

大家可以用这道题练练手。
熟能生巧，\(NOI\)路上也是如此，加油啊！童鞋们

posted @ 2023-01-12 16:14 Phrvth 阅读(282) 评论(0) 收藏举报

刷新页面返回顶部

Phrvth

浅谈LCA问题（最近公共祖先）（四种做法）

【模板】最近公共祖先（LCA）

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

提示

浅浅分析一下？

暴力做法？

倍增

预处理

查询

\(dfs\)查询每个节点的\(2^j\)级祖先（这里用的是链式前向星存储）（不会的去查吧）

开始爬树（同一高度）

继续爬树

\(Code:\)

RMQ

直接上代码，都讲过（三个数组的预处理都会吧）

\(Code:\)

tarjan

\(Code:\)

树链剖分

公告