CS229:线性回归与梯度下降(Linear regression and gradient descent)
构建一个最基础的监督学习模型
监督学习的过程是将由输入特征X和目标变量Y组成的训练集输入,利用机器学习输出一个假设模型,使其能够用于处理新的输入,并得出符合训练集中的规律的目标变量。
特征X的数目为n,在线性回归中,我们得到一个类似y=θ0+θ1X1+θ2X2的线性模型,则为了统一,设参数向量θ=[θ0、θ1、θ2]的n+1维向量,则相应的,输入特征X也为对应的n+1维向量,其中X0=1。
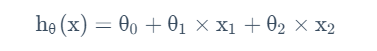
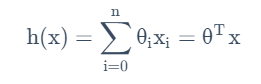
监督学习模型就是要确定这样的θ。其依据应当是使得在训练集中,h(xi)的值与yi的值要尽可能接近。故而我们建立一个这样的成本函数:
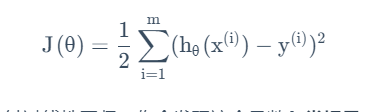
其中的1/2是为了简化数学形式。
我们使用梯度下降算法:
从某些的值开始(0向量是一个合理的默认起点)
继续改变以减小成本函数值,更新方法是:
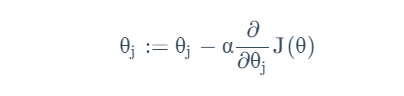
其中α为学习率,描述了参数的更新速度。这一更新应当对所有θ进行。
将求导项展开得到:
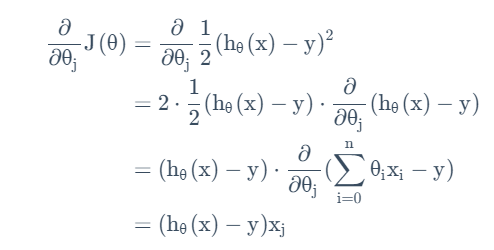
得到对单个样本的最小均方更新规则(LMS)为:
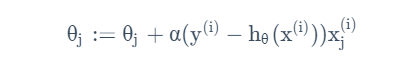
对所有样本组成的训练集,这一方法将变为:
(1)批量梯度下降法:每一次调整都使用到每一个测试项。
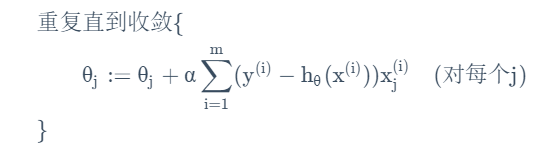
由于梯度下降法很容易被局部最小值影响,但是在这个线性回归的参数优化问题中,全局最小值只有一个,且优化函数是一个凸二次函数,故不用担心陷入局部最优。
缺点是,如果数据集过大,每次更新都需要遍历整个数据集,会带来非常大的时间开销。
(2)随机梯度下降法:每次调整只读入一个训练组,并用此来更新。
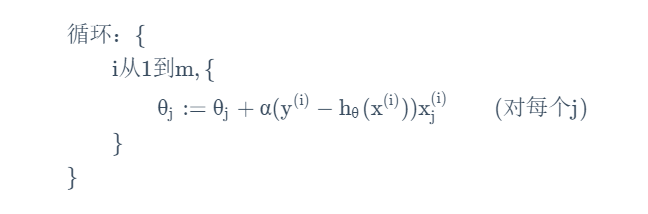
使用更加广泛,会使算法更快的获得进展(n通常比数据集小得多),但是收敛路径更嘈杂随机,将始终保持轻微的振荡,可能无法达到理论全局最优,但是会接近,且经常随着学习进行降低学习率以减小振荡。
特殊解法:法方程,但只适用于线性回归
先介绍矩阵导数和矩阵迹的一些性质
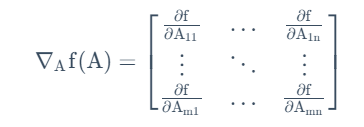
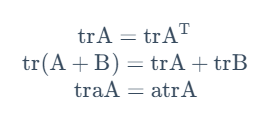
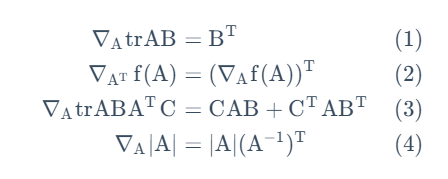
接下来将之前的模型用矩阵记号重新表述:
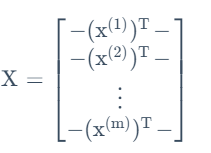
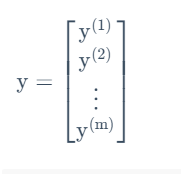
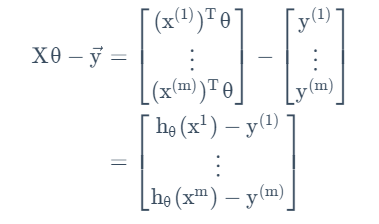
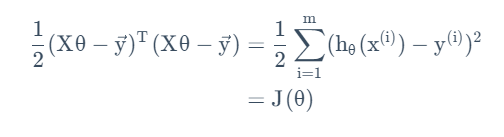
至此我们找到了原优化函数的矩阵表述。根据之前的矩阵导数和迹的性质,我们得到:
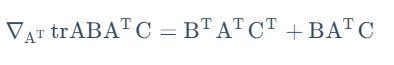
故有:
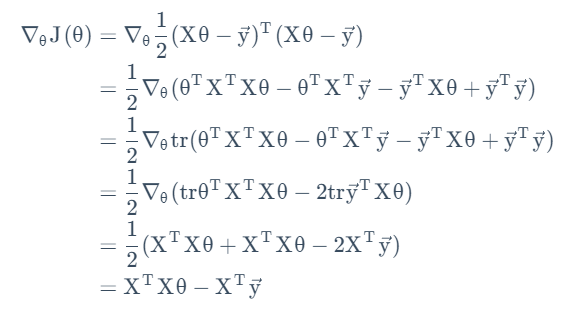
当这一导数矩阵为0向量时,达到了全局最优。这样构成的一组方程为法方程。其解为:
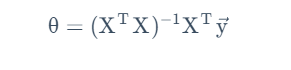



 浙公网安备 33010602011771号
浙公网安备 33010602011771号