3.Two-dimensional prefix sum二维前缀和【模板】

• [[#输入格式|输入格式]]
• [[#输出格式|输出格式]]
• [[#样例输入1|样例输入1]]
• [[#样例输出1|样例输出1]]
• [[#题解|题解]]
• [[#Code|Code]]

给定一个�n 行�m 列的整数矩阵。

有�q个询问，每个询问格式为：x1​,y1​,x2​,y2​，表示一个子矩阵的左上角和右下角的坐标。​对于每个询问，请回答子矩阵的所有数之和。

输入格式

第一行包括三个整数 n,m,q（1≤n,m≤10^{3，1≤q≤10}5）。

接下来n行，每行包括m个整数，表示整数矩阵（每个整数的取值范围为[1,105][1,105]）。

接下来q行，每行包括四个整数x1​,y1​,x2​,y2​（1≤x1​≤x2​≤n，1≤y1​≤y2​≤m），表示一个询问的左上角、右下角坐标。​

输出格式

共q行，第i（1≤i≤q）行输出第i个询问的结果。

样例输入1

7 3 2
3 5 1 
6 2 4 
7 9 10 
4 3 6 
3 9 9 
6 10 1 
9 10 4 
2 2 7 3
2 1 4 2

样例输出1

77
31

题解

• 设置一个 Prefix 二维前缀和数组

• 

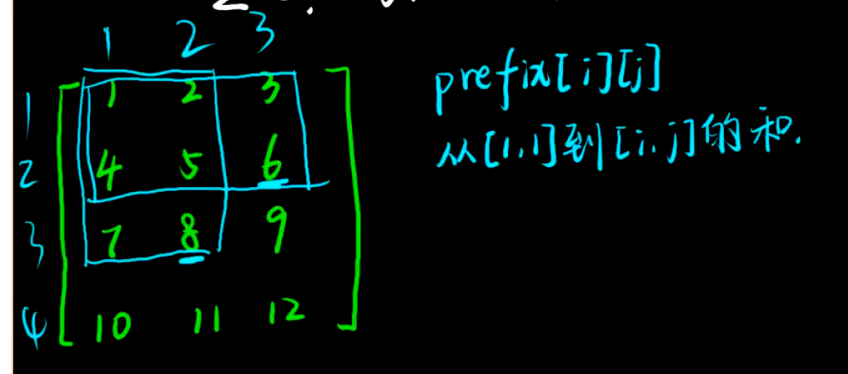
• 现在问题在于如何计算 prefix 数组中的数据

• 利用一些数形结合和动态规划的思想

• 计算方法如下图所示

• 

• 

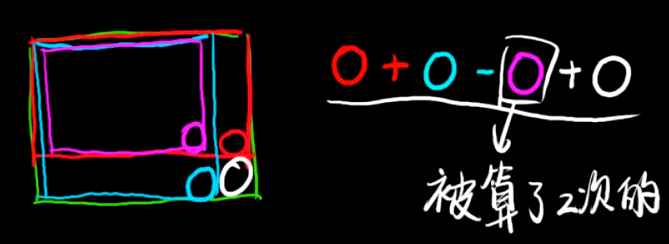
• 最后计算对应部分矩阵的加和时 x 1, y 1, x 2, y2

• 

Code

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e3 + 9;

int a[N][N], prefix[N][N];

int main() {
  ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
  int n, m, q;
  cin >> n >> m >> q;
  for (int i = 1; i <= n; ++i)
    for (int j = 1; j <= m; ++j) cin >> a[i][j];
  for (int i = 1; i <= n; ++i)
    for (int j = 1; j <= m; ++j)
      prefix[i][j] =
          prefix[i - 1][j] + prefix[i][j - 1] - prefix[i - 1][j - 1] + a[i][j];
  while (q--) {
    int x1, y1, x2, y2;
    cin >> x1 >> y1 >> x2 >> y2;
    cout << prefix[x2][y2] - prefix[x2][y1 - 1] - prefix[x1 - 1][y2] + prefix[x1 - 1][y1 - 1] << '\n';
  }

  return 0;
}