树状数组

从这边抄（借鉴）的
这是一个完整的二叉树

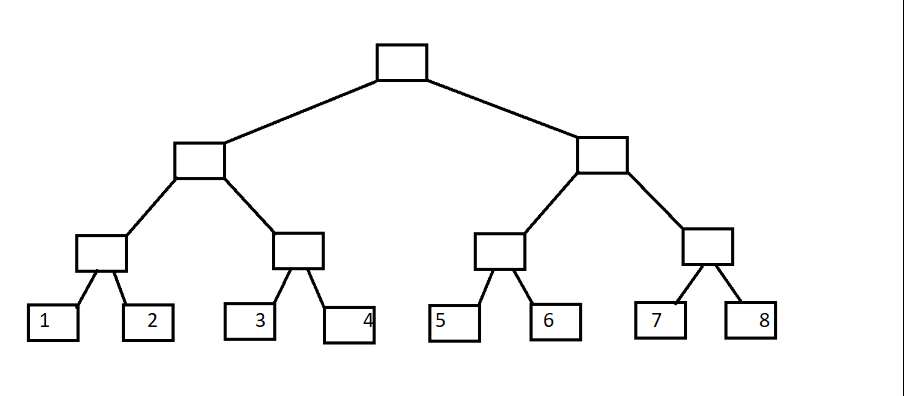
把它变成直角三角形

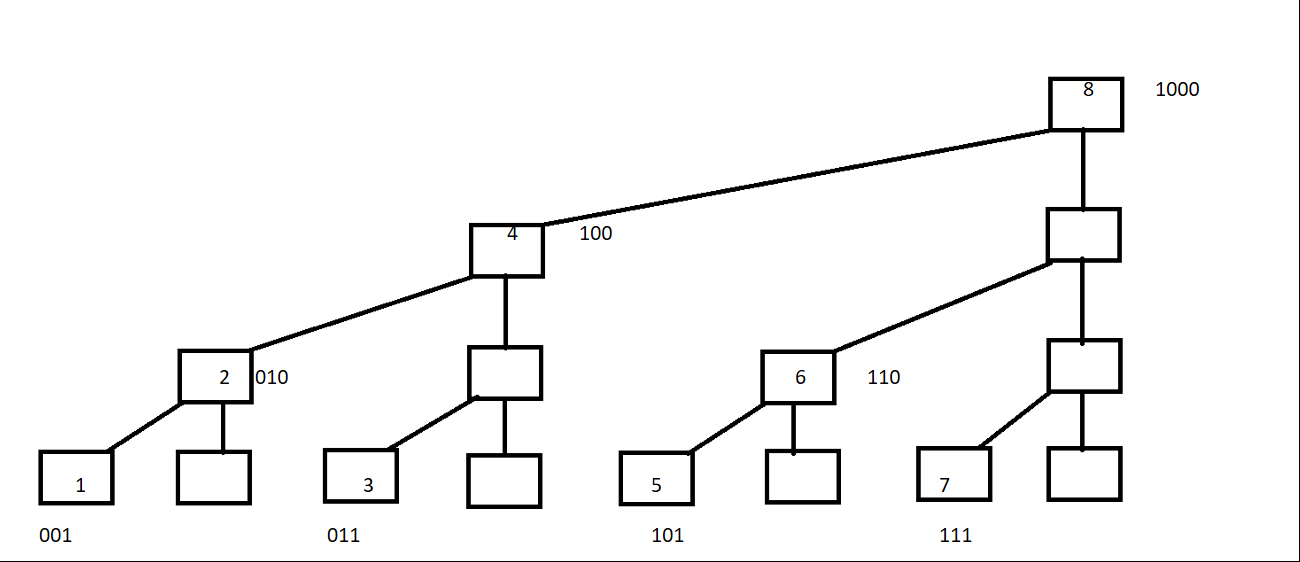
下面用一维数组对应

删掉多余的叶子

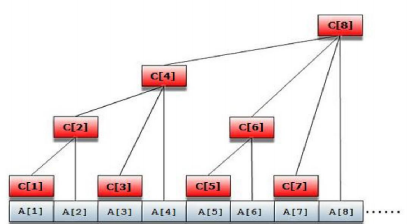
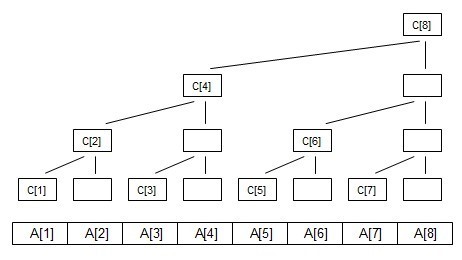
这个就是树状数组
结论：
1.设C的某个元素下标为x，则这个结点（前缀和）的管辖区间是2^k个元素（其中k为x的二进制数的末尾0的个数），且该区间的最后一个元素为Ax
2.Cx的双亲结点下标y就等于x的二进制数在最后一个1的位置上加1后得到的值。
所以C[i]=A[i-2^k+1]+A[i-2^k+2]+......A[i] （k为i的二进制中从最低位到高位连续零的长度）例如i=8（1000）时，k=3;
2^k用lowbit（i）表示
即
C[i]=A[i-lowbit(i)+1]+A[i-lowbit(i)+2]+......A[i]

点击查看代码

int lowbit(int t)
{
return t&(-t);
}
void add(int x,int y)//y就是a[i]
{
for(int i=x;i<=n;i+=lowbit(i))
 c[i]+=y;
}
int getsum(int x)
{
int ans=0;
for(int i=x;i>0;i-=lowbit(i))
 ans+=c[i];
return ans;
}

1.数列操作a（单点查询，单点更新）

跟上面差不多

#include<bits/stdc++.h>
using namespace std;
int a[150000];
int c[150000];
string str;
int n,m,num,ad;
int lowbit(int t){
	return t&(-t);
}
void add(int x,int y){
	for(int i=x;i<=n;i+=lowbit(i))
	c[i]+=y;
}
int sum(int x){
	int ans=0;
	for(int i=x;i>=1;i-=lowbit(i))
	ans+=c[i];
	return ans;
}
int cha(int x,int y){
	 x=sum(x-1),y=sum(y);
	return y-x;
}
int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];add(i,a[i]);
	}
	cin>>m;
	for(int i=1;i<=m;i++){
		cin>>str>>num>>ad;
		if(str=="SUM") cout<<cha(num,ad)<<endl;
		if(str=="ADD") add(num,ad);
	}
}

2.数列操作b（区间更新，单点查询） 区间增加不好更新，那么可以用一个b数组表示相邻两数的差值，那么更新时只会更新区间的头和区间外的头

又因为
b[2]=a[2]-a[1]
b[3]=a[3]-a[2]
…………
b[i]=a[i]-a[i-1]
所以
a[i]=b[i]+b[i-1]+……+b[1]

所以用c数组维护b数组的前缀和实际就是a数组的值

点击查看代码

#include<bits/stdc++.h>
using namespace std;
int a[150000];
int c[150000];
int b[150000];
int num[150000];
string str;
int n,m,ad,from,to,w;
int lowbit(int t){
	return t&(-t);
}
void add(int x,int y){
	for(int i=x;i<=n;i+=lowbit(i))
	c[i]+=y;
}
int sum(int x){
	int ans=0;
	for(int i=x;i>=1;i-=lowbit(i))
	ans+=c[i];
	return ans;
}
int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		b[i]=a[i]-a[i-1];
		add(i,b[i]);
	}
	cin>>m;
	for(int i=1;i<=m;i++){
		cin>>str;
		if(str=="ADD"){
			cin>>from>>to>>w;
			add(from,w);
			add(to+1,-w);
		}
		if(str=="QUERY"){
			cin>>to;
			cout<<sum(to)<<endl;
		}
	}
}

3.数列操作c（区间查询，区间更新） 需要查询区间了，很显然，不可能在b的基础上直接加个循环（要是加了为什么我不能直接打暴力） 那么我们就需要一些骚操作 我们目前要求的是

a[i]+a[i+1]+……+a[j]
可以拆成前缀和（j到1的和减i-1到1的和）
a[j]+a[j-1]+……+a[1]-a[i-1]-a[i-2]-……-a[1]
前缀和用b数组表示
b[j]+2×b[j-1]+3×b[j-2]+……+j*b[1]
化简一下
(j+1)(b[j]+b[j-1]+……+b[1])-(j×b[j]+(j-1)×b[j-1]+……+b[1])
然后分别维护两个部分就行了

点击查看代码

#include<bits/stdc++.h>
using namespace std;
long long int a[150000];
long long int c[150000];
long long int b[150000];
long long int c1[150000];
string str;
int n,m,ad,from,to,w;
int lowbit(int t){
	return t&(-t);
}
void add(int x,int y){
	for(int i=x;i<=n;i+=lowbit(i)){
		c[i]+=y;
		c1[i]+=(long long)y*x;
	}
	
}
long long sum(int x){
	long long int ans=0;long long int ans1=0;
	for(int i=x;i>=1;i-=lowbit(i)){
		ans+=c[i];ans1+=c1[i];
	}
	ans*=(x+1);
	return ans-ans1;
}
long long cha(long long  x,long long y){
	 x=sum(x-1),y=sum(y);
	return y-x;
}
int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		b[i]=a[i]-a[i-1];
		if(i==1) b[i]=a[i];
		add(i,b[i]);
	}
	cin>>m;
	for(int i=1;i<=m;i++){
		cin>>str;
		if(str=="ADD"){
			cin>>from>>to>>w;
			add(from,w);
			add(to+1,-w);
		}
		if(str=="SUM"){
			cin>>from>>to;
			cout<<sum(to)-sum(from-1)<<endl;
		}
	}//不开long long见祖宗
}