坐标dp

就是f[i][j]i和j表示的是第i行第j列
与别的没有区别
1.传纸条
往返两条路，实际上就是从起点分别走两条不相交的路，使其两条路上的总和最大
正常的话就用四层循环分别表示两条路各自点的坐标

f[x1][y1][x2][y2]=max(f[x1-1][y1][x2-1][y2],f[x1-1][y2][x2][y2-1],f[x1][y1-1][x2-1][y2],f[x1][y1-1][x2][y2-1])+a[x1][y1]+a[x2][y2]；

四层循环

#include<bits/stdc++.h>
using namespace std;
int f[51][51][51][51];int a[51][51];
int n,m;
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cin>>a[i][j];
		}
	}
	for(int i1=1;i1<=n;i1++){
		for(int j1=1;j1<=m;j1++){
			for(int i2=1;i2<=n;i2++){
				for(int j2=1;j2<=m;j2++){
					if(j2!=j1&&i2!=i1) f[i1][j1][i2][j2]//两条路除了终点不能相交
					=max({f[i1-1][j1][i2-1][j2],f[i1-1][j1][i2][j2-1],f[i1][j1-1][i2-1][j2],f[i1][j1-1][i2][j2-1]})+a[i1][j1]+a[i2][j2];
				}
			}
		}
	}
	f[n][m][n][m]=max(f[n-1][m][n][m-1],f[n][m-1][n-1][m]);
	cout<<f[n][m][n][m];
}

但由于两条路都是仅能向右向下走，所以他们的步数一定是固定的，所以可以用i推出j来 所以

f[sum][x1][x2]=max(f[sum-1][x1-1][x2],f[sum-1][x1][x2-1],f[sum-1][x1][x2],f[sum-1][x1-1][x2-1])+a[x1][sum-x1]+a[x2][sum-x2];

优化

#include<bits/stdc++.h>
using namespace std;
int f[201][51][51];int a[51][51];
int n,m,ans;
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cin>>a[i][j];
		}
	}
	for(int k=2;k<=n+m-1;k++){
		for(int i=1;i<=n;i++){
			for(int j=1;j<=n;j++){
				int j1=k+1-i;int j2=k+1-j;
				if(j1<1||j2<1) continue ;
				if(i==j) continue;
				f[k][i][j]=max({f[k-1][i][j],f[k-1][i-1][j],f[k-1][i][j-1],f[k-1][i-1][j-1]})+a[i][j1]+a[j][j2];
			}
		}
	}
	cout<<max(f[n+m-2][n][n-1],f[n+m-2][n-1][n])<<endl;
}

2.矩阵取数游戏 跟坐标好像没太大关系，更像是一个二维加一维的区间dp f[i][j][z]i表示起点，j为终点，z是某一层(因为每层互不干扰，所以说像强行加一维) 长度遍历2到len 找起点终点， f[i][j][z]=max(f[i+1][j][z]+a[z][i],f[i][j-1][z]+a[z][j]);

点击查看代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
__int128 f[101][101][101],a[200][200],sum=0;
int n,m;
void print(__int128 num){
	if(num>9)
	print(num/10);
	cout<<(char)((num%10)+'0');
}
__int128 read(){
	__int128 res=0;
	char scan[1005];
	scanf("%s",scan);
	for(int i=0;i<strlen(scan);i++){
		res*=10;res+=scan[i]-'0';
	}
	return res;
}
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			a[i][j]=read();
		}
	}
	for(int z=1;z<=n;z++){
		for(int len=1;len<=m;len++){
			for(int i=1;i+len-1<=m;i++){
				int j=i+len-1;
				f[i][j][z]=max(f[i+1][j][z]*2+a[z][i]*2,f[i][j-1][z]*2+a[z][j]*2);
			}
		}
		sum+=f[1][m][z];
	}
	print(sum);
}

3.晴天小猪 从上往下遍历，对于俩端的值特判一下 由于我存图存的是直角三角形，所以更新的位置会有不同；

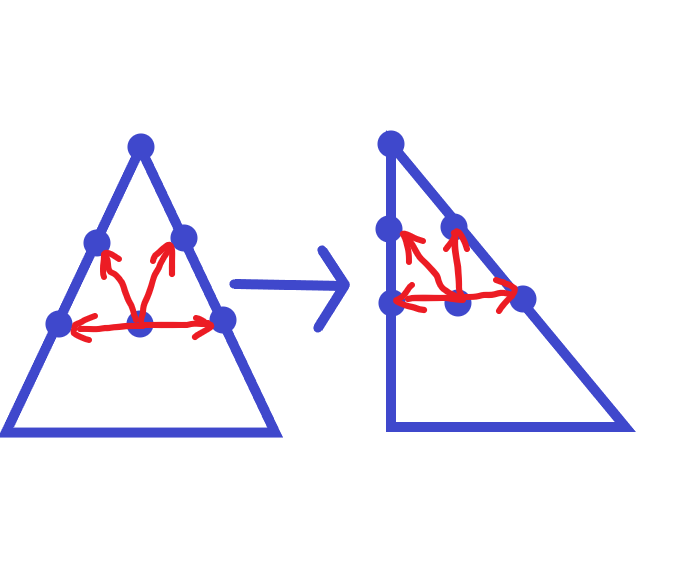
f[i][j]=min(f[i-1][j],f[i-1][j-1])+a[i][j];
f[i][j]=min(f[i][j],f[i][j-1]+a[i][j]);(左往右)
f[i][j]=min(f[i][j],f[i][j+1]+a[i][j]);(右往左)

点击查看代码

#include<bits/stdc++.h>
using namespace std;
int a[2020][2010];
int f[2022][2020];
int n;
int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=i;j++){
			cin>>a[i][j];
		}
	}
	f[1][1]=a[1][1];
	for(int i=2;i<=n;i++){
		for(int j=2;j<i;j++){
			f[i][j]=min(f[i-1][j],f[i-1][j-1])+a[i][j];//更新本层数据（两端特判）
		}
			f[i][1]=min(f[i-1][i-1],f[i-1][1])+a[i][1];
			f[i][i]=min(f[i-1][i-1],f[i-1][1])+a[i][i];
		for(int j=2;j<=i;j++){//左右两边都遍历一下，听9G说是因为某些没有被上层更新的数据会影响后面数据的更新，所以要两边更新
			f[i][j]=min(f[i][j],f[i][j-1]+a[i][j]);
		}
		f[i][1]=min(f[i][1],f[i][i]+a[i][1]);
		for(int j=i-1;j>=1;j--){
			f[i][j]=min(f[i][j],f[i][j+1]+a[i][j]);
		}
		f[i][i]=min(f[i][i],f[i][1]+a[i][i]);
	}
	cout<<f[n][1];
}

4.盖房子

f[i][j]=min(f[i-1][j-1],f[i-1][j],f[i][j-1])+1;
这里利用了短板效应，f[i-1][j-1]表示能往左上方拓展的边长，f[i][j-1]表示往左拓展的长度，f[i-1][j]表示往上拓展的长度
而拓展的最小边长才能是正方形边长

点击查看代码

#include<bits/stdc++.h>
using namespace std;
int a[2000][2000];
int n,m,maxn;
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cin>>a[i][j];
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if(a[i][j]){
				a[i][j]=min({a[i-1][j-1],a[i-1][j],a[i][j-1]})+1;
				maxn=max(maxn,a[i][j]);
			}
		}
	}
	cout<<maxn;
}