后缀自动机

感觉其实是把 OI-wiki 誊抄了一遍……（捂脸）

本文的证明可能有点感性，请谨慎食用。

注：下文中字符串下标均从 \(0\) 开始。

定义

SAM 是接受 \(s\) 的所有后缀的最小确定性有限状态自动机。

说人话就是，SAM 是一个有向图，边上有字符，从起点开始走，有一些终点，保证 \(s\) 的每个后缀和起点到某个终点的某条路径是一一对应的，并且节点数最小。

下面是 \(\texttt{qwqqq}\) 的 SAM：

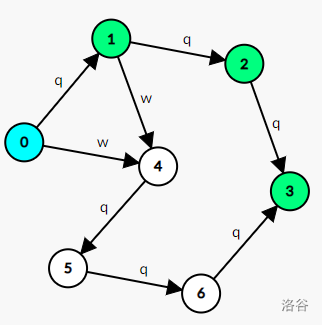
从起点 \(v_0\) 开始的每条路径和 \(s\) 的每个本质不同子串一一对应。

构建

endpos

对于 \(s\) 的一个子串 \(t\)，记 \(\text{endpos}(t)\) 为 \(t\) 在 \(s\) 中的所有结束位置。

若 \(\text{endpos}(t_1)=\text{endpos}(t_2)\)，则称 \(t_1,t_2\) 等价，记作 \(t_1\sim t_2\)，这将子串分成了若干个等价类。

不难知道 SAM 的每个节点对应着一个等价类。

引理 1

对于子串 \(t_1,t_2\)，假设 \(|t_1|\le|t_2|\)。若 \(t_1\sim t_2\)，则 \(t_1\) 是 \(t_2\) 的后缀，反之亦然。

较为显然。

引理 2

对于子串 \(t_1,t_2\)，假设 \(|t_1|\le|t_2|\)。则：

\[\left\{ \begin{aligned} &\text{endpos}(t_2)\subseteq\text{endpos}(t_1)&t_1\in\text{suffix}(t_2)\\ &\text{endpos}(t_2)\cap\text{endpos}(t_1)=\varnothing&\text{otherwise} \end{aligned} \right. \]

证明：若 \(\text{endpos}(t_2)\cap\text{endpos}(t_1)\not=\varnothing\)，那么 \(t_1,t_2\) 在某个相同位置结束，则 \(t_1\in\text{suffix}(t_2)\)，由引理 \(1\) 即得。

引理 3

将同一等价类内的串按照长度从大到小排序，那么每个串都是前一个串的后缀，并且所有串的长度恰好覆盖一个区间 \([l,r]\)。

证明：由引理 1 得等价类中没有等长的子串，设 \(t_1\) 为其中最短的串，\(t_2\) 为其中最长的串，考虑长度在 \([|t_1|,|t_2|]\) 中的 \(t_2\) 的后缀 \(t_3\)，由引理 2 得 \(\text{endpos}(t_2)\subseteq\text{endpos}(t_3)\subseteq\text{endpos}(t_1)\)，又因为 \(t_1\sim t_2\)，因此 \(t_3\) 也在等价类中。

link

对于 SAM 中不是起点的状态 \(v\)，其对应某个等价类，选取其中最长的串 \(t\) 作为代表元，那么等价类中其余的串都是它的后缀。

设 \(t'\) 是 \(t\) 的最长后缀，且满足 \(t'\not\sim t\)。设 \(t'\) 所在等价类为 \(v'\)，则记后缀链接 \(\text{link}(v)=v'\) 表示 \(t\) 的最长后缀的另一个等价类的状态。

定义空串（即初始状态 \(v_0\) 对应的子串）的 \(\text{endpos}\) 为 \(\{-1,0,\dots,n-1\}\)。

引理 4

后缀链接构成一棵树，根节点为 \(v_0\)。

证明：每次向 \(\text{link}(v)\) 移动都会使得 \(t\) 变短，最终一定会到达 \(v_0\)。

引理 5

按照 \(\text{endpos}\) 的包含关系建出的树（由引理 2 可知这确实是一棵树）和 \(\text{link}\) 连出的树相同，称其为 parent tree。

证明：对于状态 \(v\not=v_0\)，有 \(\text{endpos}(v)\subsetneq\text{endpos}(\text{link}(v))\)，不难看出 \(\text{link}\) 构成的树其实就是 \(\text{endpos}\) 的包含关系所建成的一棵树。

对于状态 \(v\)，与其匹配的子串中最长的记为 \(\text{longest}(v)\)，记 \(\text{len}(v)=|\text{longest}(v)|\)；同理，记最短的为 \(\text{shortest}(v)\)，记 \(\text{minlen}(v)=|\text{shortest}(v)|\)。

由定义得 \(\text{minlen}(v)=\text{len}(\text{link}(v))+1\)。

算法

SAM 的构建是在线的，支持往末尾加入字符。在过程中，只需要维护 \(\text{len}\)、\(\text{link}\) 以及每个状态的转移边，要标记出合法的终止状态，只需要从 \(s\) 对应的状态一直跳 \(\text{link}\) 即可（当然也可以同时维护，见代码）。

初始时 SAM 仅包含初始状态 \(0\)，定义 \(\text{len}(0)=0,\text{link}(0)=-1\)。

令 \(\text{last}\) 为添加字符 \(c\) 前整串所在的状态，新建状态 \(\text{cur}\)，令 \(\text{len}(\text{cur})=\text{len}(\text{last})+1\)，考虑 \(\text{link}(\text{cur})\) 的值。

从 \(\text{last}\) 开始，如果当前点已存在字符 \(c\) 的转移，就停下并记它为 \(p\)；否则添加一个标记为 \(c\)、到 \(\text{cur}\) 的转移。

如果没有找到 \(p\)（到达了 \(-1\)），则将 \(\text{link}(\text{cur})\) 赋值为 \(0\)。

否则设其通过 \(c\) 转移到 \(q\)，若 \(\text{len}(q)=\text{len}(p)+1\)，则将 \(\text{link}(\text{cur})\) 赋值为 \(q\)。

否则复制 \(q\) 到一个新的状态 \(\text{copy}\)，并将 \(\text{len}(\text{copy})\) 赋值为 \(\text{len}(p)+1\)，将 \(\text{link}(q)\) 和 \(\text{link}(\text{cur})\) 均更新为 \(\text{copy}\)。然后从 \(p\) 开始跳 \(\text{link}\)，如果当前点有标记为 \(c\)、目标为 \(q\) 的转移，则将其重定向至 \(\text{copy}\)，否则跳出。

最后，将 \(\text{last}\) 更新为 \(\text{cur}\)。

容易发现 SAM 的状态数不会超过 \(2n-1\)，上界在 \(\texttt{ab}\cdots\texttt{bb}\) 时取得。

还能得到 SAM 的转移数不会超过 \(3n-4\)，类似上面的情况分讨每条边 \(\text{len}(p)\) 和 \(\text{len}(q)\) 的关系即可。

原理

创建 \(\text{cur}\) 相当于新建了一个 \(\text{endpos}\) 等价类，其最长的子串显然是 \(s+c\)，故 \(\text{len}(\text{cur})=\text{len}(\text{last})+1\)。

随后访问原串 \(s\) 的所有后缀，尝试添加标记为 \(c\) 的转移。如果一直没有找到 \(p\)，说明没有后缀的前缀是 \(c\)，故 \(c\) 之前没有出现过，即 \(s\) 中不存在 \(s+c\) 的任何一个非空后缀，此时 \(\text{link}(\text{cur})=0\)。

否则找到一条转移 \((p,q,c)\)，显然 \(q\) 中包含 \(\text{longest}(p)+c\)，但不一定为 \(\text{longest}(q)\)。

如果 \(\text{len}(q)=\text{len}(p)+1\)，可以推出 \(q\) 中最长的子串是 \(\text{longest}(p)+c\)，根据定义可以知道 \(\text{longest}(p)+c\) 就是最长的、不在 \(\text{cur}\) 中的 \(\text{longest}(\text{cur})\) 的后缀，因此 \(\text{link}(\text{cur})=q\)。

否则需要将 \(\text{longest}(p)+c\) 及其在 \(q\) 中的所有后缀拿出来，分出一个新的等价类 \(\text{copy}\)，赋值 \(\text{link}(\text{cur})=\text{copy}\)，同时需要重定向 \(q\) 中 \(\text{longest}(p)+c\) 的后缀的转移，即跳 \(\text{link}\) 直到 \(-1\) 或者没有标记为 \(c\) 的到 \(q\) 的转移。

最小性

实际上，SAM 所有节点构成了一棵 parent tree，每个节点的 endpos 集合都不一样就已经最小了。

OI-wiki 里提到了一个叫 Myhill–Nerode Theorem 的东西，这是什么啊？

Talk is cheap. Show me the code.

然而代码的下标是从 \(1\) 开始的。

int tag[N << 1];
struct SAM {
	struct node { int len, link, nxt[26]; };
	int cnt, last; node t[N << 1];
	SAM() { cnt = 1; }
	void insert(int c) {
		int cur = ++cnt;
		t[cur].len = t[last].len + 1, tag[cur] = 1;
		int p = last;
		while (p && !t[p].nxt[c]) t[p].nxt[c] = cur, p = t[p].link;
		if (!p) t[cur].link = 1;
		else {
			int q = t[p].nxt[c];
			if (t[q].len == t[p].len + 1) t[cur].link = q;
			else {
				int copy = ++cnt;
				t[copy] = t[q], t[copy].len = t[p].len + 1;
				while (p && t[p].nxt[c] == q) t[p].nxt[c] = copy, p = t[p].link;
				t[q].link = t[cur].link = copy;
			}
		}
		last = cur;
	}
} sam;

可以把上面代码中的 int nxt[26] 换成 unordered_map<int, int> nxt，可以做到 \(\mathcal O(n)\) 时空复杂度，不过很少需要这么写。

应用

字符串匹配

直接在 SAM 上面走即可，如果走不动了就不匹配。这样同时可以得到模式串在文本串上出现的最长前缀。时间复杂度为 \(\mathcal O(n+\sum m)\)。

本质不同子串个数

答案为 SAM 上从 \(0\) 开始的路径条数，在 DAG 上做拓扑序 dp 即可：

\[f_u=\sum_{u\rightarrow v}f_v+1 \]

答案为 \(f_0-1\)，时间复杂度为 \(\mathcal O(n)\)。

另外，在 SAM 上做拓扑排序并不需要把图建出来，只需要借助 \(\text{len}\) 桶排即可：

for (int i = 1; i <= cnt; i++) buc[t[i].len]++;
for (int i = 1; i <= cnt; i++) buc[i] += buc[i - 1];
for (int i = 1; i <= cnt; i++) id[buc[t[i].len]--] = i;

\(\text{id}_i\) 即表示拓扑序为 \(i\) 的点编号。

本质不同子串长度和

在求出 \(f\) 的基础上，设 \(g_u\) 为从 \(u\) 开始能走出的所有本质不同子串的长度之和，有：

\[g_u=\sum_{u\rightarrow v}(g_v+f_v) \]

加上 \(f_v\) 的原因是所有路径均增加了长度 \(1\)。时间复杂度为 \(\mathcal O(n)\)。

出现次数

答案为 \(\text{endpos}\) 大小，即 parent tree 上子树的结束位置个数。

最小表示法

将字符串复制一倍，现在要找所有长度为 \(n\) 的子串中字典序最小的，从起点开始走 \(n\) 条最小的边即可。

本质不同第 k 小子串

先求出 \(f\) 表示本质不同子串个数，类似平衡树找第 \(k\) 小，只不过这里是找到 \(26\) 个儿子中对应的那一个走。

第 k 小子串

需要更改上面 \(f\) 的定义，变成位置不同子串个数，转移式变为：

\[f_u=\sum_{u\rightarrow v}f_v+|\text{endpos}_u| \]

\(\text{endpos}\) 的大小也可以通过拓扑序累加得到。

Code：

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e6 + 5;
struct node { int len, link, nxt[26]; } t[N];
int op, k, cnt = 1, last = 1, buc[N], id[N], siz[N], sum[N];
char s[N];
void insert(int c) {
	int cur = ++cnt;
	t[cur].len = t[last].len + 1, siz[cur] = 1;
	int p = last;
	while (p && !t[p].nxt[c]) t[p].nxt[c] = cur, p = t[p].link;
	if (!p) t[cur].link = 1;
	else {
		int q = t[p].nxt[c];
		if (t[q].len == t[p].len + 1) t[cur].link = q;
		else {
			int copy = ++cnt;
			t[copy] = t[q], t[copy].len = t[p].len + 1;
			while (p && t[p].nxt[c] == q) t[p].nxt[c] = copy, p = t[p].link;
			t[q].link = t[cur].link = copy;
		}
	}
	last = cur;
}
void topsort() {
	for (int i = 1; i <= cnt; i++) buc[t[i].len]++;
	for (int i = 1; i <= cnt; i++) buc[i] += buc[i - 1];
	for (int i = 1; i <= cnt; i++) id[buc[t[i].len]--] = i;
	for (int i = cnt; i >= 1; i--) siz[t[id[i]].link] += siz[id[i]];
	for (int i = 1; i <= cnt; i++) sum[i] = op ? siz[i] : (siz[i] = 1);
	siz[1] = sum[1] = 0;
	for (int i = cnt; i >= 1; i--) for (int j = 0; j < 26; j++) sum[id[i]] += sum[t[id[i]].nxt[j]];
}
void kth(int p, int k) {
	if (k <= siz[p]) return; k -= siz[p];
	for (int i = 0, c; i < 26; i++) {
		if (!(c = t[p].nxt[i])) continue;
		if (k > sum[c]) k -= sum[c];
		else return putchar('a' + i), kth(c, k), void();
	}
}
signed main() {
	scanf("%s%lld%lld", s, &op, &k);
	for (int i = 0; s[i]; i++) insert(s[i] - 'a');
	topsort();
	if (sum[1] >= k) kth(1, k); else puts("-1");
}

双串最长公共子串

建出 \(S_1\) 的 SAM，在上面跳，初始时 \(p=1\)，\(\text{len}=0\)，如果有一条边是 \(S_{2}[i]\) 就跳过去并且 \(\text{len}\) 加上 \(1\)，否则一直跳 \(\text{link}\) 并且 \(\text{len}\) 减去 \(1\) 直到跳到有 \(S_2[i]\) 的边或者跳到 \(1\)。

int calc(char s[]) {
	int p = 1, len = 0, ans = 0;
	for (int i = 0, c; s[i]; i++) {
		c = s[i] - 'a';
		if (t[p].nxt[c]) p = t[p].nxt[c], len++;
		else {
			while (p && !t[p].nxt[c]) p = t[p].link;
			if (p) len = t[p].len + 1, p = t[p].nxt[c];
			else p = 1, len = 0;
		}
		ans = max(ans, len);
	}
	return ans;
}

多串最长公共子串

选择最短的串建立 SAM（为了保证复杂度不超过 \(\mathcal O(\sum|S|)\)），剩下每个串在上面跳，记录 \(\text{mx}_u\) 表示到达点 \(u\) 的最大匹配长度，对每个串取 \(\min\)。由于点 \(u\) 能匹配的话它的所有祖先也可以匹配，因此 \(\text{mx}\) 数组还需要对子树内取 \(\max\)。

代码里没有选择最短串。

void upd(char s[]) {
	int p = 1, len = 0;
	for (int i = 0, c; s[i]; i++) {
		c = s[i] - 'a';
		while (p && !t[p].nxt[c]) p = t[p].link, len = t[p].len;
		if (p) len++, p = t[p].nxt[c], mx[p] = max(mx[p], len);
		else p = 1, len = 0;
	}
	for (int i = cnt, u, f; i >= 1; i--) {
		u = id[i], f = t[u].link;
		mx[f] = max(mx[f], min(mx[u], t[f].len)), mn[u] = min(mn[u], mx[u]), mx[u] = 0;
	}
}
int main() {
	scanf("%s", s);
	for (int i = 0; s[i]; i++) insert(s[i] - 'a');
	topsort();
	memset(mn, 0x3f, sizeof(mn));
	while (scanf("%s", s) != EOF) upd(s);
	for (int i = 1; i <= cnt; i++) ans = max(ans, mn[i]);
	printf("%d", ans);
}

posted @ 2025-02-28 21:44 Pentimentqwq 阅读(62) 评论(0) 收藏举报

刷新页面返回顶部