多项式

注：下文 \(x/y\) 均表示 \(\left\lfloor\dfrac xy\right\rfloor\)，即除法向下取整。

FFT

引入

设想一下，现在要做两个多项式的乘法 \(f(x)g(x)\)，相信每个人都会 \(\mathcal O(n^2)\) 暴力做，但这两个多项式的次数达到了 \(10^6\) 级别，需要 \(\mathcal O(n\log n)\) 的做法。

有一个经典的思想是构造群同构，FFT 和 FWT 等都利用了这个思想。这里就是把多项式变成若干个点值，对应点值相乘之后再变回去。

但如果选一些平凡的点值，例如 \(0\sim n\)，求值和还原都不好做，因此需要选一些特殊的点值。因为求值时出现了很多 \(x^n\) 这种东西，单位根 \(\omega_n\) 是一个不错的选择。

复数

首先默认你会复数，这里还是简单说一下，令 \(i=\sqrt{-1}\)，称形如 \(z=a+bi\ (a,b\in\mathbb R)\) 的数为复数，\(a\) 为实部，\(b\) 为虚部。可以定义复数的加减乘除：

\((a+bi)+(c+di)=(a+c)+(b+d)i\)；
\((a+bi)-(c+di)=(a-c)+(b-d)i\)；
\((a+bi)(c+di)=(ac-bd)+(ad+bc)i\)；
\(\dfrac{a+bi}{c+di}=\dfrac{(a+bi)(c-di)}{(c+di)(c-di)}=\dfrac{(ac+bd)+(-ad+bc)i}{c^2+d^2}\)。

将实部作为 \(x\) 坐标，虚部作为 \(y\) 坐标，那么复数和平面上的点可以一一对应。

定义辐角是其对应点与原点的连线和 \(x\) 轴正半轴的夹角，可以得到复数乘法的几何意义为长度相乘、辐角相加，因此也可用 \((r,\theta)\) 即极坐标表示一个复数。

\(n\) 次单位根指的是单位圆周上的 \(n\) 等分点，即：

\[\omega_n=\cos\dfrac{2\pi}{n}+i\sin\dfrac{2\pi}{n} \]

结合图像理解：

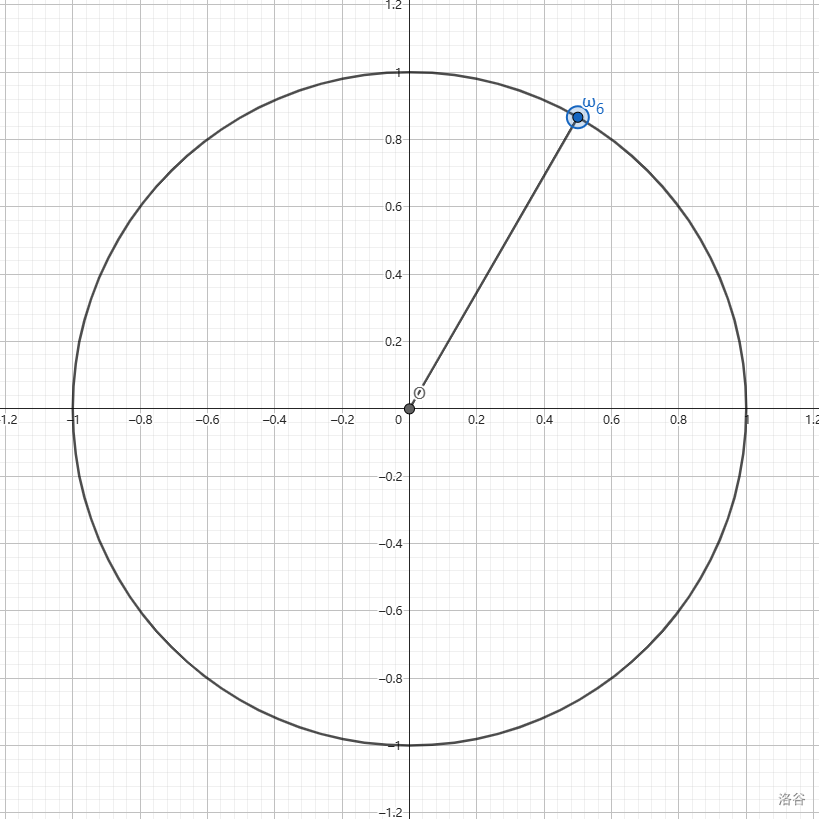
\(\omega_n\) 有一个性质，就是 \(\omega_{nm}^m=\omega_n\)，考虑复数乘法的几何意义不难得到。实际上乘上 \(\omega_n\) 就相当于转了 \(\dfrac{2\pi}{n}\)。

最初的 DFT

DFT（离散傅里叶变换）指的就是求出 \(f(x)\) 在单位根 \(\omega_n^0,\omega_n^1,\sim,\omega_n^{n-1}\) 处的点值。首先将 \(n\) 补至 \(2^m\) 的形式方便求解，随后列出式子（以 \(n=8\) 为例）：

\[f(x)=a_0+a_1x+a_2x^2+a_3x^3+a_4x^4+a_5x^5+a_6x^6+a_7x^7 \]

考虑按奇偶分治：

\[f(x)=(a_0+a_2x^2+a_4x^4+a_6x^6)+(a_1x+a_3x^3+a_5x^5+a_7x^7) \]

右边提一个 \(x\) 出来：

\[f(x)=(a_0+a_2x^2+a_4x^4+a_6x^6)+x(a_1+a_3x^2+a_5x^4+a_7x^6) \]

设 \(g(x)=a_0+a_2x+a_4x^2+a_6x^3,h(x)=a_1+a_3x+a_5x^2+a_7x^3\)，那么有：

\[f(x)=g(x^2)+xh(x^2) \]

代入 \(\omega_n^k\) 和 \(\omega_n^{k+n/2}\) 可得：

\[f(\omega_n^k)=g(\omega_n^{2k})+\omega_n^kh(\omega_n^{2k})=g(\omega_{n/2}^k)+\omega_n^kh(\omega_{n/2}^k) \]

\[f(\omega_n^{k+n/2})=g(\omega_n^{2k+n})+\omega_n^{k+n/2}h(\omega_n^{2k+n})=g(\omega_{n/2}^k)-\omega_n^kh(\omega_{n/2}^k) \]

因此只要求出了 \(g(\omega_{n/2}^k)\) 与 \(h(\omega_{n/2}^k)\)，便可求出 \(f(\omega_n^k)\) 和 \(f(\omega_n^{k+n/2})\)，递归分治求解即可，时间复杂度为 \(\mathcal O(n\log n)\)。

倍增优化

上面的做法是递归的，常数会比较大（实际上在模板题上光荣地 TLE 了），考虑改成非递归形式，例如先把所有系数在原数组上按照最终的顺序排布好，然后再倍增地合并。

位运算优化

以 \(n=8\) 为例：

\[[0,1,2,3,4,5,6,7] \]

\[[0,2,4,6][1,3,5,7] \]

\[[0,4][2,6][1,5][3,7] \]

\[[0][4][2][6][1][5][3][7] \]

可以发现 \(i\) 最终的位置刚好是 \(i\) 二进制翻转后的结果。设 \(\text{tax}(x)\) 表示 \(x\) 二进制翻转后的结果，为了递推地求解，对于 \(x\)，将其右移一位、翻转、再右移一位，最后补上个位翻转后的数即可，有递推式：

\[\text{tax}(x)=\text{tax}(x/2)/2+(x\bmod2)\cdot\dfrac{n}{2} \]

得到 \(\text{tax}\) 数组后，即可将每个 \(i\) 移到其对应的位置，然后倍增求解。

蝶形运算优化

使用位运算将每个 \(i\) 移到对应的位置后，\(g(\omega_{n/2}^k)\) 的值存储在下标为 \(k\) 的位置，而 \(h(\omega_{n/2}^k)\) 的值存储在下标为 \(k+\dfrac n2\) 的位置，刚好是求解 \(f(\omega_{n}^k)\) 和 \(f(\omega_{n}^{k+n/2})\) 要用到的位置，因此直接在原位置赋值即可。

IDFT

粗略地写一下。

即从点值重新得到多项式。设 \(f(\omega_n^i)=y_i\)，定义多项式：

\[\hat f(x)=\sum_{i=0}^{n-1}y_ix^i \]

直接将 \(\omega_n^k\) 代入 \(\hat f(x)\)，最终可以得到：

\[\hat f(\omega_n^k)=\sum_{i=0}^{n-1}a_i\sum_{j=0}^{n-1}\omega_n^{(i+k)j} \]

后面那一坨当且仅当 \(n|i+k\) 时为 \(n\)，否则为 \(0\)，因此有：

\[\hat f(\omega_n^k)=a_{n-k}n \]

那么对 \(y\) 做 DFT 之后翻转 \([1,n-1]\)，最后将每个数除以 \(n\) 即可。

完整代码：（P3803）

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 4194309;
const double pi = acos(-1);
typedef complex<double> comp;
int n, m, N = 1, tax[MAXN];
comp F[MAXN], G[MAXN];
void qread(int &a) {
	a = 0;
	char ch = getchar();
	while (ch < '0' || ch > '9') ch = getchar();
	while (ch >= '0' && ch <= '9') a = a * 10 - '0' + ch, ch = getchar();
}
void init(int n) {
	int x = n / 2, p = 2;
	tax[0] = 0, tax[1] = x;
	for (int i = 2; i <= n; i *= 2) {
		x /= 2;
		for (int j = 0; j < i; j++) tax[p++] = tax[j] | x;
	}
}
void FFT(int n, comp A[]) {
	for (int i = 1; i < n; i++) {
		if (i < tax[i]) swap(A[i], A[tax[i]]);
	}
	for (int i = 2; i <= n; i *= 2) {
		comp w(cos(pi / i * 2), sin(pi / i * 2)), W(1, 0);
		for (int l = 0, r = i - 1; r <= n; l += i, r += i) {
			comp tmp = W;
			for (int p = l; p < l + i / 2; p++) {
				comp x = A[p] + tmp * A[p + i / 2], y = A[p] - tmp * A[p + i / 2];
				A[p] = x, A[p + i / 2] = y, tmp *= w;
			}
		}
	}
}
int main() {
	qread(n), qread(m);
	for (int i = 0, x; i <= n; i++) qread(x), F[i] = x;
	for (int i = 0, x; i <= m; i++) qread(x), G[i] = x;
	while (N <= n + m) N *= 2;
	init(N), FFT(N, F), FFT(N, G);
	for (int i = 0; i < N; i++) F[i] *= G[i];
	FFT(N, F), reverse(F + 1, F + N);
	for (int i = 0; i <= n + m; i++) printf("%d ", int(F[i].real() / N + 0.5));
}

NTT

现在要在模 \(998244353\) 意义下求解多项式乘法，不能有浮点数精度误差，怎么做？

考虑使用模意义下的某个数 \(g\) 来代替 \(\omega_n\)。有一个东西叫原根，满足 \(x^{\varphi(p)}\equiv1\pmod p\)，例如 \(998244353\) 的一个原根是 \(3\)，满足 \(3^{998244352}\equiv1\pmod{998244353}\)。由于 \(998244352=2^{23}\times7\times17\)，并且我们将 \(n\) 补成了 \(2^m\) 的形式，直接使用 \(3^{\frac{p-1}{n}}\) 代替 \(\omega_n\) 即可。

完整代码：（P3803）

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAXN = 4194310, mod = 998244353;
int n, m, N = 1, F[MAXN], G[MAXN], tax[MAXN];
inline void qread(int &a) {
	a = 0;
	char ch = getchar();
	while (ch < '0' || ch > '9') ch = getchar();
	while (ch >= '0' && ch <= '9') a = a * 10 - '0' + ch, ch = getchar();
}
inline int qpow(int a, int b) {
	int ans = 1;
	while (b) {
		if (b & 1) ans = (ll)ans * a % mod;
		a = (ll)a * a % mod, b >>= 1;
	}
	return ans;
}
inline void init(int n) {
	int x = n / 2, p = 2;
	tax[0] = 0, tax[1] = x;
	for (int i = 2; i <= n; i *= 2) {
		x /= 2;
		for (int j = 0; j < i; j++) tax[p++] = tax[j] | x;
	}
}
inline void NTT(int n, int A[]) {
	for (int i = 1; i < n; i++) {
		if (i < tax[i]) swap(A[i], A[tax[i]]);
	}
	for (int i = 2; i <= n; i *= 2) {
		int w = qpow(3, (mod - 1) / i);
		for (int l = 0; l < n; l += i) {
			int tmp = 1;
			for (int p = l; p < l + (i >> 1); p++) {
				int x = (A[p] + (ll)tmp * A[p + (i >> 1)] % mod) % mod, y = (A[p] - (ll)tmp * A[p + (i >> 1)] % mod) % mod;
				A[p] = x, A[p + (i >> 1)] = y, tmp = (ll)tmp * w % mod;
			}
		}
	}
}
signed main() {
	qread(n), qread(m);
	for (int i = 0, x; i <= n; i++) qread(F[i]);
	for (int i = 0, x; i <= m; i++) qread(G[i]);
	while (N <= n + m) N *= 2;
	init(N), NTT(N, F), NTT(N, G);
	for (int i = 0; i < N; i++) F[i] = (ll)F[i] * G[i] % mod;
	NTT(N, F), reverse(F + 1, F + N);
	int inv = qpow(N, mod - 2);
	for (int i = 0; i <= n + m; i++) printf("%lld ", ((ll)F[i] * inv % mod + mod) % mod);
}

多项式乘法逆

一个经典的做法是倍增。

假设现在已经求出了 \(f(x)\) 在 \(\bmod\,x^{\lceil n/2\rceil}\) 意义下的逆元 \(g_0(x)\)，有：

\[f(x)g(x)\equiv f(x)g_0(x)\equiv 1\pmod{x^{\lceil n/2\rceil}} \]

即：

\[g(x)-g_0(x)\equiv0\pmod{x^{\lceil n/2\rceil}} \]

平方：

\[g^2(x)-2g(x)g_0(x)+g_0^2(x)\equiv 0\pmod{x^n} \]

两边同乘 \(f\) 并移项：

\[g(x)=f(x)g_0^2(x)-2g_0(x)\pmod{x^n} \]

NTT 搞一下这个东西，时间复杂度为 \(\mathcal O(n\log n)\)。

poly inv(const poly &a, int n) {
	poly b;
	if (n == 1) {
		b.resize(1);
		b[0] = qinv(a[0], mod);
		return b;
	}
	b = inv(a, n + 1 >> 1);
	int l = getrev(n << 1);
	b.resize(l);
	poly A;
	A.resize(l);
	for (int i = 0; i < n; i++) A[i] = a[i];
	for (int i = n; i < l; i++) A[i] = 0;
	NTT(A, l, 0), NTT(b, l, 0);
	for (int i = 0; i < l; i++) b[i] = ll(mod + 2 - (ll)A[i] * b[i] % mod) * b[i] % mod;
	NTT(b, l, 1);
	b.resize(n);
	return b;
}

posted @ 2025-02-12 17:24 Pentimentqwq 阅读(43) 评论(0) 收藏举报

刷新页面返回顶部

多项式

FFT

引入

复数