做题!
Tags:
【树】【博弈】【匹配】【构造】【贪心】【映射】【Trie】【组合数学】【计数 dp】【距离】【随机化】【期望】【拉格朗日插值】【数论】
P5801 [SEERC 2019] Game on a Tree
\(\color{#3498db}9.4\) tag:【树】【博弈】【匹配】
Trick:树上博弈,考虑完美匹配。
以防读题读错了,这个题中的棋子可以移动到任意没走过的祖先节点,不只是父亲节点。
首先有一个类似的问题:假如棋子只能移动到相邻节点,考虑完美匹配的存在性:
- 如果存在完美匹配,先手不管选哪个点,后手都可以选它的匹配点,这样后手一直有点选,所以后手必胜;
- 否则先手可以选择一个非匹配点,显然其它点都是匹配点(不然就存在增广路,可以多一条匹配边),那么就变成了第一种情况,只不过先后手交换了,因此先手必胜。
这个题也差不多,区别在于 \(u\) 不仅可以和其相邻点匹配,还可以和它的任意祖先匹配,树形 dp,设 \(f_u\) 表示 \(u\) 子树内最少还剩多少个未匹配的点,转移是容易的。
#include <bits/stdc++.h>
using namespace std;
const int N = 100005;
int n, f[N]; vector<int> G[N];
void dfs(int u, int fa) {
for (int v : G[u]) if (v != fa) dfs(v, u), f[u] += f[v];
if (f[u]) f[u]--; else f[u] = 1;
}
int main() {
scanf("%d", &n);
for (int i = 1, u, v; i < n; i++) scanf("%d%d", &u, &v), G[u].push_back(v), G[v].push_back(u);
dfs(1, 0), printf("%s", f[1] ? "Alice" : "Bob");
}
P8976 「DTOI-4」排列
\(\color{#52c41a}8.4\) tag:【构造】【贪心】
整个序列的和是固定的,那么只需要让前一半的和不小于且尽可能接近 \(a\) 即可。
实际上只要有解,那就一定可以使得前一半之和恰好等于 \(a\)。使用调整法构造,一开始让前一半是 \(\left[1,\dfrac n2\right]\) 的数,从右往左依次调整,设 \(\text{mx}\) 表示当前最大的可用数,现在枚举到了 \(i\),还差 \(d\),如果 \(\text{mx}-i\ge d\),那就直接将 \(p_i\) 设为 \(i+d\) 即可,完事;否则将 \(p_i\) 设为 \(\text{mx}\),这时 \(\text{mx}\leftarrow\text{mx}-1\)。这样可以保证和恰好为 \(a\),并且每个数不重复。
最后剩下的数就放在右半边,记得判无解。
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e5 + 5;
int T, n, a, b, p[N], h, sum, mx, now, d;
bool vis[N];
signed main() {
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
cin >> T;
while (T--) {
cin >> n >> a >> b;
h = n >> 1, sum = n * (n + 1) >> 1, mx = n, now = h * (h + 1) >> 1, d = a - now;
for (int i = 1; i <= h; i++) p[i] = i;
for (int i = h; i && d > 0; i--) {
if (mx - i < d) now += mx - i, d -= mx - i, p[i] = mx--;
else now += d, p[i] = i + d, d = 0;
}
if (d > 0 || sum - now < b) { cout << -1 << '\n'; continue; }
memset(vis + 1, 0, n);
for (int i = 1; i <= h; i++) cout << p[i] << ' ', vis[p[i]] = 1;
for (int i = 1; i <= n; i++) if (!vis[i]) cout << i << ' ';
cout << '\n';
}
}
P10753 [COI 2022/2023] Bliskost
\(\color{#ffc116}7\) tag:【映射】
Trick:判断是否本质相同,找不变量/找最小状态。
找最小状态这个思想比较常用,例如判断两个字符串是否循环同构,可以把它们的最小表示法求出来,就能直接判断是否相等了。
这个题中,一个字符串显然可以被变成 \(\texttt{aa...ax}\) 的形式,例如 \(\texttt{abc}\rightarrow\texttt{aab}\),\(\texttt{ced}\rightarrow\texttt{acd}\rightarrow\texttt{aab}\),只需要判断最后一个字符是否相等即可。
令 \(\texttt a=0\),\(\texttt b=1\),以此类推,容易得到最后一个字母为:
直接算即可。
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
int n, q, a1, a2;
char s1[N], s2[N];
int main() {
scanf("%d%d%s%s", &n, &q, s1 + 1, s2 + 1);
for (int i = 1; i <= n; i++) (n - i & 1) ? a1 -= s1[i] - 'a' : a1 += s1[i] - 'a';
for (int i = 1; i <= n; i++) (n - i & 1) ? a2 -= s2[i] - 'a' : a2 += s2[i] - 'a';
puts((a1 % 26 + 26) % 26 == (a2 % 26 + 26) % 26 ? "da" : "ne");
int x; char y;
while (q--) {
scanf("%d %c", &x, &y);
(n - x & 1) ? a1 += s1[x] - 'a' : a1 -= s1[x] - 'a';
s1[x] = y;
(n - x & 1) ? a1 -= s1[x] - 'a' : a1 += s1[x] - 'a';
puts((a1 % 26 + 26) % 26 == (a2 % 26 + 26) % 26 ? "da" : "ne");
}
}
P6018 [Ynoi2010] Fusion tree
\(\color{#9d3dcf}10.4\) tag:【Trie】
首先考虑如果没有操作 1 怎么做,对于每个节点 \(u\),将其儿子节点的权值建出 01-Trie,操作 2 时在父节点处删除旧值并插入新值即可,操作 3 查询的是 Trie 上的全局异或值,记录一下有多少个数第 \(i\) 位是 \(1\) 即可。
现在有操作 1,对于父亲做单点修改,会影响祖父的 Trie;对于儿子,在 Trie 上做全局 \(+1\) 即可。时间复杂度为 \(\mathcal O(n\log V)\)。
#include <bits/stdc++.h>
using namespace std;
#define il inline
#define IOSIZE (1 << 20)
char buf[IOSIZE], *p1 = buf, *p2 = buf;
#define gc() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, IOSIZE, stdin), p1 == p2) ? EOF : *p1++)
il int read() { int x = 0; char c = '%'; while (c < '0' || c > '9') c = gc(); while (c >= '0' && c <= '9') x = x * 10 + c - '0', c = gc(); return x; }
const int N = 5e5 + 5;
int n, m, a[N], fa[N], tag[N], rt[N], tot, ch[N * 20][2], cnt[N * 20], num[N][20];
vector<int> G[N];
il void ins(int u, int x) {
int p = rt[u]; cnt[p]++;
for (int i = 0, o; i < 20; i++) {
o = x >> i & 1, num[u][i] += o;
if (!ch[p][o]) ch[p][o] = ++tot;
p = ch[p][o], cnt[p]++;
}
}
il void del(int u, int x) {
int p = rt[u]; cnt[p]--;
for (int i = 0, o; i < 20; i++) {
o = x >> i & 1, num[u][i] -= o;
p = ch[p][o], cnt[p]--;
}
}
il void upd(int u) {
int p = rt[u];
for (int i = 0; i < 20; i++) {
if (!cnt[p]) return;
num[u][i] += cnt[ch[p][0]] - cnt[ch[p][1]];
swap(ch[p][0], ch[p][1]), p = ch[p][0];
}
}
il int qry(int u) {
int sum = 0;
for (int i = 0; i < 20; i++) if (num[u][i] & 1) sum |= 1 << i;
return sum;
}
il int val(int u) { return a[u] + tag[fa[u]]; }
il void dfs(int u, int f) {
fa[u] = f, rt[u] = ++tot;
for (int i = 0, s = G[u].size(), v; i < s; i++) if ((v = G[u][i]) != f) dfs(v, u), ins(u, a[v]);
}
int main() {
n = read(), m = read();
for (int i = 1, u, v; i < n; i++) u = read(), v = read(), G[u].push_back(v), G[v].push_back(u);
for (int i = 1; i <= n; i++) a[i] = read();
dfs(1, 0);
int op, x, y;
while (m--) {
op = read(), x = read();
if (op == 1) {
tag[x]++, upd(x);
int f = fa[x], ff = fa[f];
if (f) {
if (ff) del(ff, val(f)), a[f]++, ins(ff, val(f));
else a[f]++;
}
} else if (op == 2) {
y = read();
int f = fa[x];
if (f) del(f, val(x)), a[x] -= y, ins(f, val(x));
else a[x] -= y;
} else {
int f = fa[x];
if (f) cout << (val(f) ^ qry(x)) << '\n';
else cout << qry(x) << '\n';
}
}
}
P4456 [CQOI2018] 交错序列
\(\color{#ffc116}7\) tag:【组合数学】
插空法,答案即为:
线性筛筛出 \(i^a\) 和 \(i^b\),组合数需要用卢卡斯定理算。
#include <bits/stdc++.h>
using namespace std;
#define il inline
typedef long long ll;
const int N = 1e7 + 5;
struct Mod {
ll m, p;
il void init(int pp) { m = ((__int128)1 << 64) / pp; p = pp; }
il ll operator()(ll x) { return x - ((__int128(x) * m) >> 64) * p; }
} mod;
int n, a, b, M, fac[N], inv[N], tot, pri[N], pwa[N], pwb[N];
bool vis[N];
il int qpow(int a, int b) {
int c = 1;
while (b) { if (b & 1) c = mod((ll)c * a); a = mod((ll)a * a), b >>= 1; }
return c;
}
il void init(int n) {
fac[0] = 1;
for (int i = 1; i <= n; i++) fac[i] = mod((ll)fac[i - 1] * i);
inv[n] = qpow(fac[n], M - 2);
for (int i = n - 1; ~i; i--) inv[i] = mod((ll)inv[i + 1] * (i + 1));
pwa[0] = (a == 0), pwb[0] = (b == 0), pwa[1] = 1, pwb[1] = 1;
for (int i = 2, k, p; i <= n; i++) {
if (!vis[i]) pri[++tot] = i, pwa[i] = qpow(i, a), pwb[i] = qpow(i, b);
for (int j = 1; j <= tot && (k = i * (p = pri[j])) <= n; j++) {
vis[k] = 1, pwa[k] = mod((ll)pwa[i] * pwa[p]), pwb[k] = mod((ll)pwb[i] * pwb[p]);
if (!(i % p)) break;
}
}
}
il int C(int n, int m) { return n < m || m < 0 ? 0 : mod(mod((ll)fac[n] * inv[n - m]) * inv[m]); }
il int Lucas(int n, int m) { return n < M && m < M ? C(n, m) : mod((ll)C(mod(n), mod(m)) * C(n / M, m / M)); }
int main() {
scanf("%d%d%d%d", &n, &a, &b, &M);
mod.init(M), init(n + 1); int nn = (n + 1) >> 1, ans = 0;
for (int i = 0; i <= nn; i++) ans = mod(ans + Lucas(n - i + 1, i) * mod((ll)pwa[n - i] * pwb[i]));
printf("%d", (ans % M + M) % M);
}
P4977 毒瘤之神异之旅
\(\color{#3498db}9.8\) tag:【计数 dp】
Trick:分拆类问题,转成 Ferrers 图求解。
Ferrers 图是这样一个东西:
1
11
1111
1111
11111
1111111
代表一个无序分拆方案。上图代表的方案为 \(1+2+4+4+5+7\)。
将一个 Ferrers 图沿着对角线翻转,得到的新 Ferrers 图称为原图的共轭,新分拆称为原分拆的共轭。上图的共轭如下所示:
1
1
11
1111
1111
11111
111111
其共轭代表的方案为 \(1+1+2+4+4+5+6\)。
本题中,直接决策第 \(i\) 个数是多少不太好做,将其对称后,去掉了行数的限制,并且增加了每行宽度的上界 \(K\),较容易求解。设 \(f_{i,j}\) 表示使用了 \(i\) 个 \(1\),最后一行有 \(j\) 个 \(1\) 的方案数,可以得到转移方程:
统计答案的时候,枚举末尾有多少个 \(j\) 即可,答案为:
滚动数组一下。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 10005, p = 1e9 + 7;
int n, k, m, pw[N], f[2][N], ans;
int qpow(int a, int b) {
int c = 1;
while (b) { if (b & 1) c = (ll)c * a % p; a = (ll)a * a % p, b >>= 1; }
return c;
}
int main() {
scanf("%d%d%d", &n, &k, &m);
for (int i = 1; i <= n; i++) pw[i] = qpow(i, m);
f[0][0] = 1;
for (int j = 0, x, y; j < k; j++) {
x = j & 1, y = x ^ 1;
memset(f[y], 0, sizeof(f[y]));
for (int i = j; i <= n; i++) f[y][i] = (f[x][i - 1] + f[y][i - j - 1]) % p;
for (int i = 1; i <= n; i++) {
if (i * (k - j) <= n) ans = (ans + (ll)f[x][n - i * (k - j)] * pw[i]) % p;
}
}
cout << ans;
}
P6143 [USACO20FEB] Equilateral Triangles P
\(\color{#3498db}9.4\) tag:【距离】
先画出一个曼哈顿等边三角形 \(ABC\):
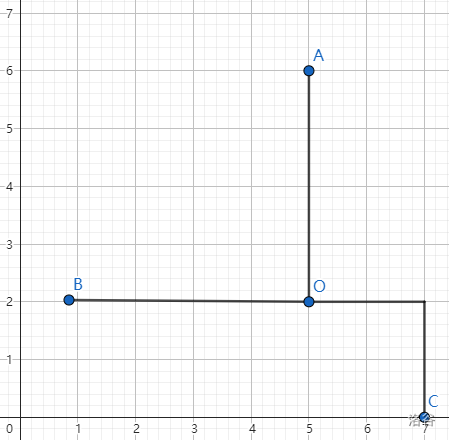
找到一个点 \(O\) 使得 \(\text{dis}(A,O)=\text{dis}(B,O)=\text{dis}(C,O)\),称其为曼哈顿外心。
枚举点 \(A\) 和 \(\text{dis}(A,O)\),这样可以在一个方向上确定点 \(B\)。可以发现 \(C\) 的合法取值在一条斜线上,做一个斜向的前缀和即可。
#include <bits/stdc++.h>
using namespace std;
const int N = 605, M = N * N;
int n, s[N][N], tot, x[M], y[M];
char a[N][N], t[N][N];
long long ans;
void turn() {
memcpy(t, a, sizeof(t));
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) a[j][i] = t[n - i + 1][j];
}
}
void calc() {
memset(s, 0, sizeof(s));
for (int i = 1; i < n << 1; i++) {
for (int j = 1; j < n << 1; j++) s[i][j] = s[i - 1][j + 1] + a[i][j];
}
tot = 0;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) if (a[i][j]) x[++tot] = i, y[tot] = j;
}
for (int i = 1, x1, y1, x2, y2; i <= tot; i++) {
for (int j = 1; j <= n; j++) {
x1 = x[i], y1 = y[i], x2 = x1 - j, y2 = y1 + j;
if (x2 >= 0 && y2 <= n && a[x2][y2]) ans += s[x1 + j][y1 + j] - s[x1][y1 + (j << 1)];
}
}
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%s", a[i] + 1);
for (int j = 1; j <= n; j++) a[i][j] = (a[i][j] == '*');
}
for (int i : {0, 1, 2, 3}) calc(), turn();
printf("%lld", ans);
}
P4581 [BJOI2014] 想法
\(\color{#0e1d69}{11.0}\) tag:【随机化】【期望】
好像有什么神秘的叫 Hyperloglog 的东西,不会。
有向图可达点数不可做的原因在于会算重,那就整一些不会算重的,例如 \(\min\)?
有一个比较好猜的结论:在 \([0,1]\) 中均匀随机选 \(n\) 个数,其最小值期望为 \(\dfrac{1}{n+1}\)。
给每个点随机 \([0,1]\) 中的实数权值,先把每个点可达的点中的权值最小值算出来,多次试验取平均值,然后直接用上面的式子计算出估计值即可。
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5, T = 200;
int n, m, u[N], v[N];
double w[N], s[N];
int main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
for (int i = m + 1; i <= n; i++) cin >> u[i] >> v[i];
for (int t = 1; t <= T; t++) {
for (int i = 1; i <= m; i++) w[i] = 1.0 * rand() / RAND_MAX;
for (int i = m + 1; i <= n; i++) s[i] += (w[i] = min(w[u[i]], w[v[i]])) / T;
}
for (int i = m + 1; i <= n; i++) cout << int(1.0 / s[i] - 0.5) << '\n';
}
P4463 [集训队互测 2012] calc
\(\color{#9d3dcf}10.6\) tag:【计数 dp】【拉格朗日插值】
很 educational 的一道题。
要互不相等,那就让它递增吧,最后再乘个 \(n!\)。
设 \(f_{i,j}\) 表示前 \(i\) 个数,第 \(i\) 个数 \(\le j\) 的贡献和,有:
初始值为 \(f_{0,j}=1\)。
不幸的是 \(k\le10^9\),于是这个做法就死了。但 \(n\) 很小,这启示我们使用复杂度在 \(\mathcal O(n^2)\) 到 \(\mathcal O(n^3)\) 之间的做法。
手动写出 \(n=0,1,2,\dots\) 的表达式:
发现 \(f_{n,j}\) 是关于 \(j\) 的 \(2n\) 次多项式。实际上有:
那就暴算出 \(f_{n,1}\sim f_{2n+1}\) 的值,拉格朗日插值即可,时间复杂度为 \(\mathcal O(n^2)\)。
#include <bits/stdc++.h>
using namespace std;
#define il inline
typedef long long ll;
const int N = 505;
il int qpow(int a, int b, const int P) {
int c = 1;
while (b) { if (b & 1) c = (ll)c * a % P; a = (ll)a * a % P, b >>= 1; }
return c;
}
int k, n, p, fac = 1, f[N][N << 1];
int main() {
scanf("%d%d%d", &k, &n, &p); const int P = p;
for (int i = 1; i <= n; i++) fac = (ll)fac * i % P;
int u = min(n << 1 | 1, k);
for (int i = 0; i <= u; i++) f[0][i] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= u; j++) f[i][j] = (f[i][j - 1] + (ll)j * f[i - 1][j - 1]) % P;
}
if (k <= u) return printf("%lld", (ll)f[n][k] * fac % P), 0;
int ans = 0;
for (int i = 1, up, dn; i <= u; i++) {
up = f[n][i], dn = 1;
for (int j = 1; j <= u; j++) {
if (i != j) up = (ll)up * (k - j + p) % P, dn = (ll)dn * (i - j + p) % P;
}
ans = (ans + (ll)up * qpow(dn, P - 2, P)) % P;
}
printf("%lld", ((ll)ans * fac) % P);
}
P6060 [加油武汉] 传染病研究
\(\color{#9d3dcf}10.4\) tag:【数论】
这个 \(T\le10^4\) 很容易误导你去想 \(\mathcal O(T\sqrt n)\),其实也可以做不过挺麻烦,有一种 \(\mathcal O((T+n)\omega(n))\) 的简洁做法,所以为什么不把 \(T\) 也开到 \(10^7\) 呢?
首先把 \(\sigma(n^k)\) 的式子写出来,假设 \(n=\prod\limits_{i=1}^mp_i^{c_i}\):
可以发现这是一个关于 \(k\) 的低次多项式,\(10^7\) 以内次数不超过 \(8\)。
线性筛可以直接把每个多项式求出来,查询的时候直接算即可。
#include <bits/stdc++.h>
using namespace std;
#define il inline
typedef long long ll;
const int N = 1e7 + 5, Mod = 998244353;
int T, n, k, ans, tot, pri[N], fac[N], cnt[N], md[N], f[N][9];
il int mod(int x) { return x >= Mod ? x - Mod : x; }
il void sieve(int n) {
f[1][0] = 1;
for (int i = 2, k, p, x, ck; i <= n; i++) {
if (!fac[i]) pri[++tot] = i, fac[i] = i, cnt[i] = 1, md[i] = i, f[i][0] = f[i][1] = 1;
for (int j = 1; j <= tot && (k = i * (p = pri[j])) <= n; j++) {
fac[k] = p;
if (fac[i] == p) {
ck = cnt[k] = cnt[i] + 1, md[k] = md[i] * p, x = i / md[i], f[k][0] = 1;
for (int i1 = 1; i1 <= 8; i1++) f[k][i1] = (f[x][i1] + (ll)f[x][i1 - 1] * ck) % Mod;
break;
}
cnt[k] = 1, md[k] = p, f[k][0] = 1;
for (int i1 = 1; i1 <= 8; i1++) f[k][i1] = mod(f[i][i1] + f[i][i1 - 1]);
}
}
for (int i = 2; i <= n; i++) for (int j = 0; j <= 8; j++) f[i][j] = mod(f[i][j] + f[i - 1][j]);
}
int main() {
sieve(N - 1);
// return 0;
scanf("%d", &T);
while (T--) {
scanf("%d%d", &n, &k);
ans = 0;
for (int i = 8; ~i; i--) ans = ((ll)ans * k + f[n][i]) % Mod;
printf("%d\n", ans);
}
}
P9406 [POI 2020/2021 R3] Nawiasowania
\(\color{#3498db}9.6\) tag:【构造】【贪心】
将左括号作为 \(1\),右括号作为 \(-1\),合法条件是任意位置的前缀和不小于 \(0\)。那么在保证排列后的括号串合法的情况下,原串中一定是左括号越靠左越容易合法。令字典序最小的合法串为“最优串”。
考虑由 \(n-2\) 的构造得到 \(n\) 的构造,先在末尾新增两个右括号,然后在序列中选择一个右括号变成左括号,要求修改后仍然合法。
可以发现除了 \(s_n\) 外的右括号都可以改成左括号,那用一个堆维护目前可以改成左括号的最小位置即可。
小吐槽:这个题如果说“输出字典序最小的解”就会更好想一些,至少对我这种乐色来说/kk。
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
int n, a[N], c; char s[N];
priority_queue<int, vector<int>, greater<int> > Q;
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]), s[i] = ')';
Q.push(a[1]);
for (int i = 1; i <= n >> 1; i++) {
s[Q.top()] = '('; Q.pop();
if (i < n >> 1) Q.push(a[i << 1]), Q.push(a[i << 1 | 1]);
}
for (int i = 1; i <= n; i++) {
s[i] == '(' ? c++ : c--;
if (c < 0) return puts("NIE"), 0;
}
puts(c ? "NIE" : s + 1);
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号