python 作业23 列表6

问题：

0.请使用列表推导式，创建一个内容为 [1, 4, 9, 16, 25, 36] 的列表？

a = [(i+1)**2 for i in range(6)]

 

 

1.请使用列表推导式，创建一个内容为 [[0, 2], [1, 3], [2, 4], [3, 5], [4, 6], [5, 7]] 的列表？

[[i-1,i+1] for i in range(1,7)]

 

 

2.请将下面的列表推导式转换为循环的形式实现？

>>> double = [c * 2 for c in "FishC"]
>>> double
['FF', 'ii', 'ss', 'hh', 'CC']

 

double = [ i*2 for i in "FishC"]

 

 

3. 请将下面的循环转换为列表推导式的形式实现？

>>> matrix = [[1, 2, 3],
...           [4, 5, 6],
...           [7, 8, 9]]
>>> diag = []
>>> for i in range(len(matrix)):
...     i *= matrix[i][i]
...     diag.append(i)
...
>>> diag
[0, 5, 18]

 

dlag = [i*matrix[i][i] for i in range(len(matrix))]

 

 

4.请问下面代码执行后，变量 x 和 y 的值分别是什么？

>>> x = "FishC"
>>> y = [x for x in "123"]

 x

'FishC'
y
['1', '2', '3']

5.解决一下课堂中遗留的问题吧，如何获取矩阵从右上角到左下角这条对角线上的元素？

>>> matrix = [[1, 2, 3],
...           [4, 5, 6],
...           [7, 8, 9]]

 

matrix = [[1, 2, 3],
          [4, 5, 6],
          [7, 8, 9]]
a = [matrix[i][len(matrix)-1-i] for i in range(len(matrix))]

 

动动手：

0.打印杨辉三角形

杨辉三角形是中国古代数学的杰出研究成果之一，是我国北宋数学家贾宪于 1050 年首先发现并使用的。而后南宋数学家杨辉在《详解九章算法》一书中记载并保存了“贾宪三角形“。因此，贾宪三角形又被称为杨辉三角形

 

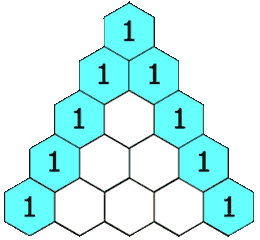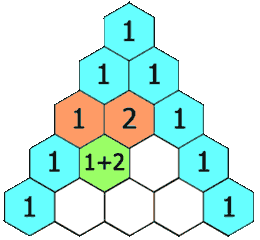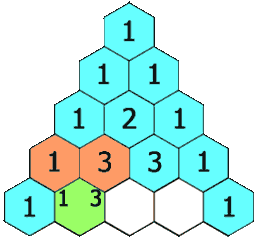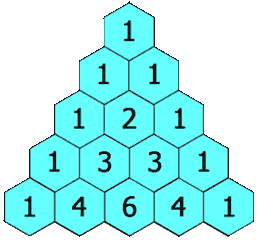
 从上面的动图我们可以得出一个道公式：杨辉三角形第i行j列的值 = 第 (i-1) 行 (j-1) 列的值 + 第 (i-1) 行 (j) 列的值8

 

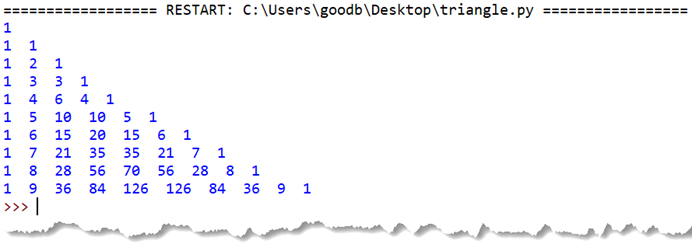
# 初始化杨辉三角形
# 创建一个10*10的二维列表，并将所有的元素初始化为0
triangle = []
for i in range(10):
    triangle.append([])
    for j in range(10):
        triangle[i].append(0)
    
# 计算杨辉三角形
# 根据观察，我们知道杨辉三角形左右两边的元素均为1
for i in range(10):
    triangle[i][0] = 1
    triangle[i][i] = 1
    
# 第i行j列的值 = 第(i-1)行(j-1)列的值 + 第(i-1)行(j)列的值
for i in range(2, 10):
    for j in range(1, i):
        triangle[i][j] = triangle[i-1][j-1] + triangle[i-1][j]
    
# 输出杨辉三角形
for i in range(10):
    for j in range(i+1):
        print(triangle[i][j], end='  ')
    print()

 

 

 

1.在不使用超纲姿势的前提下，修改代码，将杨辉三角形按下图的形式打印：

 

 

# 初始化杨辉三角形
# 创建一个10*10的二维列表，并将所有的元素初始化为0
triangle = []
for i in range(10):
    triangle.append([])
    for j in range(10):
        triangle[i].append(0)
    
# 计算杨辉三角形
# 根据观察，我们知道杨辉三角形左右两边的元素均为1
for i in range(10):
    triangle[i][0] = 1
    triangle[i][i] = 1
    
# 第i行j列的值 = 第(i-1)行(j-1)列的值 + 第(i-1)行(j)列的值
for i in range(2, 10):
    for j in range(1, i):
        triangle[i][j] = triangle[i-1][j-1] + triangle[i-1][j]
    
# 输出杨辉三角形
for i in range(10):
    # 因为是三角形，所以i越小，前边需要填充的TAB越多
    for k in range((10-i)//2):
        print('\t', end='')
    for j in range(i+1):
        # 要形成“隔行错开”的效果，所以我们在偶数行加4个空格
        if i % 2 == 1:
            print("    ", end='')
        # 为何要使用TAB而非空格，大家可以将下面的end='\t'改成对应的空格数即可知晓
        print(triangle[i][j], end='\t')
    print()

 

 

 

小结: