codeforces round 817

传送门

817

A

注意

不是只有题目所给的几个符合，只要满足 \(Timur\) 任意顺序都可以

B

把绿色改成蓝色，判断字符串是否相同即可

C

对每一个单词用 \(map\) 计数，再遍历看出现了几次

D

最大化情况

中线往左全是 \(R\)，中线往右全是 \(L\)

从左往中线 和 从中线往右 遍历，将能够增加的值放进 \(vector\) 中

排序，每一个k都取出目前最大的，直至 \(vector\) 为空，值就固定了

void solve()
{
    int n; cin >> n;
    string s; cin >> s;
    ll ans = 0;
    for(int i = 0; i < n; i++) {
    	if(s[i] == 'L') ans += i;
    	else ans += (n - i - 1);
    }
    vector<int> a;
    int l, r;
    if(n % 2 == 0) l = (n / 2) - 1, r = n / 2;
    else l = n / 2, r = l;
    for(int i = 0; i <= l; i++) {
    	if(s[i] == 'L') a.push_back(n - i - 1 - i);
    }
    for(int i = r; i < n; i++) {
    	if(s[i] == 'R') a.push_back(i - n + i + 1);
    }
    sort(a.begin(), a.end());
    for(int i = 0; i < n; i++) {
    	if(a.size()) {int u = a.back(); a.pop_back(); ans += u;}
    	cout << ans << ' ';
    }
    cout << '\n';
}

E

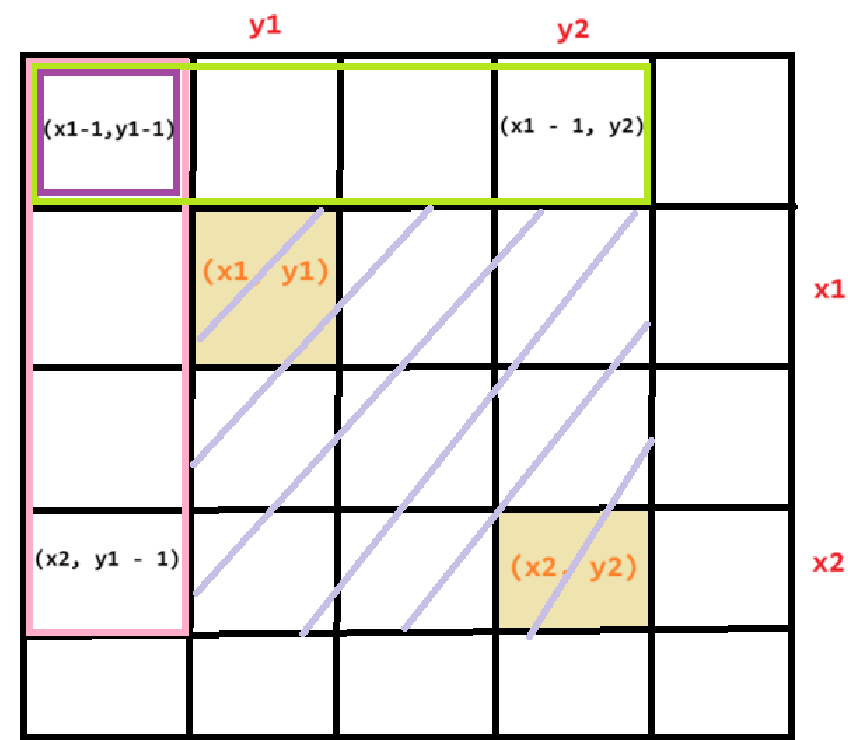
求一段区间里符合条件的矩形的面积，第一想到的是缩小范围，用多次二分，太过复杂

还是对 二维前缀和 不敏感，这样就可以直接获得面积之和

注意

\((a, b), (c, d)\) 只能取 \((a + 1, b + 1), (c - 1, d - 1)\) 这个范围

二维前缀和讲解

void solve()
{
	int n, q; cin >> n >> q;
	vector<vector<ll>> s(1010, vector<ll>(1010));
	for(int i = 0; i < n; i++) {
		int a, b; cin >> a >> b;
		s[a][b] += a * b;
	}
	for(int i = 1; i <= 1000; i++) {
		for(int j = 1; j <= 1000; j++) {
			s[i][j] = s[i][j] + s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
		}
	}
	while(q--) {
		int a, b, c, d; cin >> a >> b >> c >> d;
		a++, b++, c--, d--;
		cout << (ll)(s[c][d] - s[a - 1][d] - s[c][b - 1] + s[a - 1][b - 1]) << '\n';
	}
}

F

好麻烦的一题
不动脑子就要码量

附上别人的代码

#include<bits/stdc++.h>
#define ll long long
using namespace std;
int T,n,m,a[55][55];
char c;
void search(int i,int j){
	if(a[i+1][j]&&a[i+1][j+1]&&!a[i-1][j-1]&&!a[i-1][j]&&!a[i-1][j+1]&&
	   !a[i][j-1]&&!a[i][j+1]&&!a[i][j+2]&&!a[i+1][j-1]&&!a[i+1][j+2]&&
	   !a[i+2][j-1]&&!a[i+2][j]&&!a[i+2][j+1]&&!a[i+2][j+2]){
		a[i][j]=a[i+1][j]=a[i+1][j+1]=0;
		return ;
	}
	if(a[i+1][j-1]&&a[i+1][j]&&!a[i-1][j-1]&&!a[i-1][j]&&!a[i-1][j+1]&&
	   !a[i][j-2]&&!a[i][j-1]&&!a[i][j+1]&&!a[i+1][j-2]&&!a[i+1][j+1]&&
	   !a[i+2][j-2]&&!a[i+2][j-1]&&!a[i+2][j]&&!a[i+2][j+1]){
		a[i][j]=a[i+1][j-1]=a[i+1][j]=0;
		return ;
	}
	if(a[i][j+1]&&a[i+1][j+1]&&!a[i-1][j-1]&&!a[i-1][j]&&!a[i-1][j+1]&&
	   !a[i-1][j+2]&&!a[i][j-1]&&!a[i][j+2]&&!a[i+1][j-1]&&!a[i+1][j]&&
	   !a[i+1][j+2]&&!a[i+2][j]&&!a[i+2][j+1]&&!a[i+2][j+2]){
		a[i][j]=a[i][j+1]=a[i+1][j+1]=0;
		return ;
	}
	if(a[i][j+1]&&a[i+1][j]&&!a[i-1][j-1]&&!a[i-1][j]&&!a[i-1][j+1]&&
	   !a[i-1][j+2]&&!a[i][j-1]&&!a[i][j+2]&&!a[i+1][j-1]&&!a[i+1][j+1]&&
	   !a[i+1][j+2]&&!a[i+2][j-1]&&!a[i+2][j]&&!a[i+2][j+1]){
		a[i][j]=a[i][j+1]=a[i+1][j]=0;
		return ;
	}
}
void solve(){
	scanf("%d%d",&n,&m);
	memset(a,0,sizeof(a));
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cin>>c;
			if(c=='*') a[i][j]=1;
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if(a[i][j]==1) search(i,j);
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if(a[i][j]==1){
				printf("NO\n");
				return ;
			}
		}
	}
	printf("YES\n");
}
int main(){
	scanf("%d",&T);
	while(T--) solve();
    return 0;
}

G

奇数位和偶数位异或和相等 ---> 总异或和为0

设前 \(n - 3\) 个数中 奇数位异或和为 \(j\) ，偶数位异或和为 \(o\)，倒数第三位设为 \(k\) ^ \(x\) ^ \(y\)，\(k = j\) ^ \(o\)，后面两位为\(x, y\)

奇数位异或和为 $j $ ^ \(x\)， 偶数位异或和为 $o $ ^ \(y\) ^ \(j\) ^ \(o\) ^ \(x\) ^ \(y\)

所以最后相等

void solve()
{
    int n; cin >> n;
    int k = 0;
    for(int i = 0; i < n - 3; i++) {
    	cout << i << ' ';
    	k ^= i;
    }
    int x = 1 << 24, y = 1 << 25;
    cout << (k ^ x ^ y) << ' ' << x << ' ' << y << '\n';
}