Rudolf and k Bridges

Rudolf and k Bridges

题目

大致题意

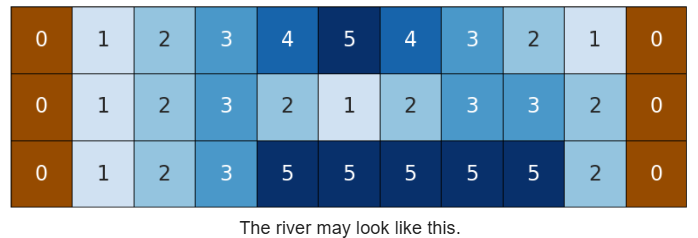
上图为俯视图

有一个\(nXm\)的网格，下标从\(1-n\) 以及从 \(1-m\)，\((i, j)\) 的值就是这个这垂直一格水的深度

现在要安装支架，有几个信息：

• \((i, 1)\) 和 \((i, m)\) 处必须要安装

• 相邻支架的距离不能超过 \(d\), 相邻距离为 \(abs(j - i) - 1\)

• 在一个格子里安装支架的成本是 \(aij + 1\)

• 要连续安装 \(k\) 行，求出 最小成本

思路

求连续k行最小成本 --> 求每一行的最小成本，再利用滑动窗口看哪个连续 \(k\) 行的总成本最小

---

求每一行的最小成本

既要保证距离不超过 \(d\)，又要最小

就可以使用小根堆 以及利用 单调队列的思想
假设第i个格子是最后一个，那么以它结尾的值就是 现在队列的最小值 ➕它的值 ➕ 1，所以我们就要将每一个格子的总值都算出来，最后汇总时使用（\(j==m\) 时）

---

如何实现❓

在队列中的个数小于 \(d + 2\) 的时候就可以将现在的值入队，入队的是以它结尾的总成本，以及它的下标

如果队列中的个数超过了 \(d + 2\)，那么就要 \(pop\) 掉最小值，实时更新当前位置的最小总成本

由于 \((i, 1)\) 和 \((i, m)\) 都要安装，所以在每一行开始遍历的时候直接 \(push(1, 1)\) 解决了第一个；在 \(j == m\) 的时候就直接结束这一行，将最终总成本放到 \(sum\)数组中

最后用滑动窗口求出连续 \(k\) 行的最小成本之和

代码

// Problem: E. Rudolf and k Bridges
// Contest: Codeforces - Codeforces Round 933 (Div. 3)
// URL: https://codeforces.com/contest/1941/problem/E
// Memory Limit: 256 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include <iostream>
#include <cmath>
#include <cstdlib>
#include <algorithm>
#include <string>
#include <stack>
#include <queue>
#include <unordered_map>
#include <map>
#include <vector>
#include <cstring>
#include <bitset>
#include <set>

using namespace std;
using ll = long long;
using PII = pair<ll, int>;

int gcd(int a, int b) {return b == 0 ? a : gcd(b, a % b);}
int lcm(int a, int b) {return a / gcd(a, b) * b;}

void solve()
{
    int n, m, k, d; cin >> n >> m >> k >> d;
    vector<vector<int>> g(n + 1, vector<int>(m + 1));
    vector<ll> s(n + 1);
    for(int i = 1; i <= n; i++) 
    	for(int j = 1; j <= m; j++) cin >> g[i][j];
    	
    for(int i = 1; i <= n; i++) {
    	priority_queue<PII, vector<PII>, greater<PII>> pq;
    	pq.push({1, 1}); //因为（i, 1）处必须安装
    	for(int j = 2; j <= m; j++) {
    		//如果超过了d的话就pop掉最小的
    		while(pq.size() && pq.top().second < j - d - 1) pq.pop();
    		if(j == m) s[i] = pq.top().first + g[i][j] + 1; //(i, m)处必须安装
    		else pq.push({pq.top().first + g[i][j] + 1, j}); 
    	}
    }
    ll mi = 0x3f3f3f3f3f3f3f3f, sum = 0;
    for(int i = 1; i <= n; i++) {
    	sum += s[i];
    	if(i >= k) {
    		mi = min(mi, sum);
    		sum -= s[i - k + 1];
    	}
    }
    cout << mi << '\n';
}

int main()
{
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int t; cin >> t;
    //int t = 1;
    while (t--) solve();
}