『数据结构总结3：平衡树』

Preface

本文只介绍\(\mathrm{Binary\ Search\ Tree}\)和算法竞赛中常用的两种平衡树\(\mathrm{Split\ Merge\ Treap}\)，\(\mathrm{Splay}\).

Binary Search Tree

定义

二叉搜索树（\(\mathrm{Binary\ Search\ Tree}\)）是一棵带点权的有根二叉树，通常用于维护无序数集的若干操作，如查询前驱，后继，第\(k\)大值等.

\(\mathrm{BST}\)的每一个节点\(p\)满足，其左子树所有点点权小于\(v_p\)，其右子树所有点点权大于\(v_p\)，所以插入，删除，查询等操作都可以轻松实现.

遗憾的是一般的\(\mathrm{BST}\)会被单调数列卡成高度极度不平衡的形态，所有操作的最坏时间复杂度均为\(\mathcal{O}(n)\)，所以\(\mathrm{BST}\)的实际意义不大，没有必要学习代码实现.

平衡

平衡树指的是使用各种变换手段让树维持一定的形态，从而保证时间复杂度的各类\(\mathrm{BST}\). 其中平衡的定义分为两种：高度平衡和大小平衡.

\(1.\) \(\alpha-\)高度平衡：\(\mathrm{BST}\)的高度\(h\)满足\(h\leq\log_{\frac{1}{\alpha}}n\).

\(2.\) \(\alpha-\)大小平衡：\(\mathrm{BST}\)的每个节点\(p\)满足\(s(\mathrm{lson}_p)\leq \alpha \cdot s(p),s(\mathrm{rson}_p)\leq\alpha\cdot s(p)\).

这两个定义在替罪羊树的时间复杂度证明中会用到，不过本文不作讨论.

Splay

定义

伸展树（\(\mathrm{Splay}\)）又称\(\mathrm{Sleator-Tarjan\ Tree}\)，由\(\mathrm{Sleator}\)和\(\mathrm{Trajan}\)在\(1985\)年发明，用伸展操作来保证\(\mathrm{BST}\)的时间复杂度.

其中伸展操作的定义为：对于每次树上操作的节点\(x\)，我们直接使用\(\mathrm{BST}\)的方式进行操作，在操作结束后使用相等的时间复杂度进行\(\mathrm{Splay}(x)\)改变树的形态，通过势能分析法证明\(\mathrm{Splay}(x)\)的均摊复杂度正确，从而证明所有操作的均摊复杂度都是正确的.

原理

旋转

在了解如何进行伸展操作以前，我们首先要知道旋转. 旋转的定义是在保证\(\mathrm{BST}\)性质的前提下，通过重新组合父子关系的方式交换一个节点\(p\)和\(\mathrm{fa}_p\)的位置.

旋转又分为左旋和右旋，其示意图如下：

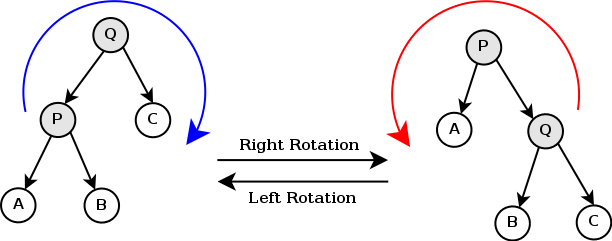
显然左右两颗树的中序遍历是一样的，所以\(\mathrm{BST}\)的性质不改变，但是\(\mathrm{P,Q}\)两个点的父子关系改变了，同时树的形态也改变了.

双旋

然而，上述一般的旋转无法保证\(\mathrm{Splay}\)操作的时间复杂度，我们还要引入双旋操作. 双旋是基于上述旋转操作的，具体来说，双旋分为两种：

\(1.\) 当节点\(p\)的两代祖先都与其位于同一条链上时，先旋转\(\mathrm{fa}_p\)，再旋转\(p\).

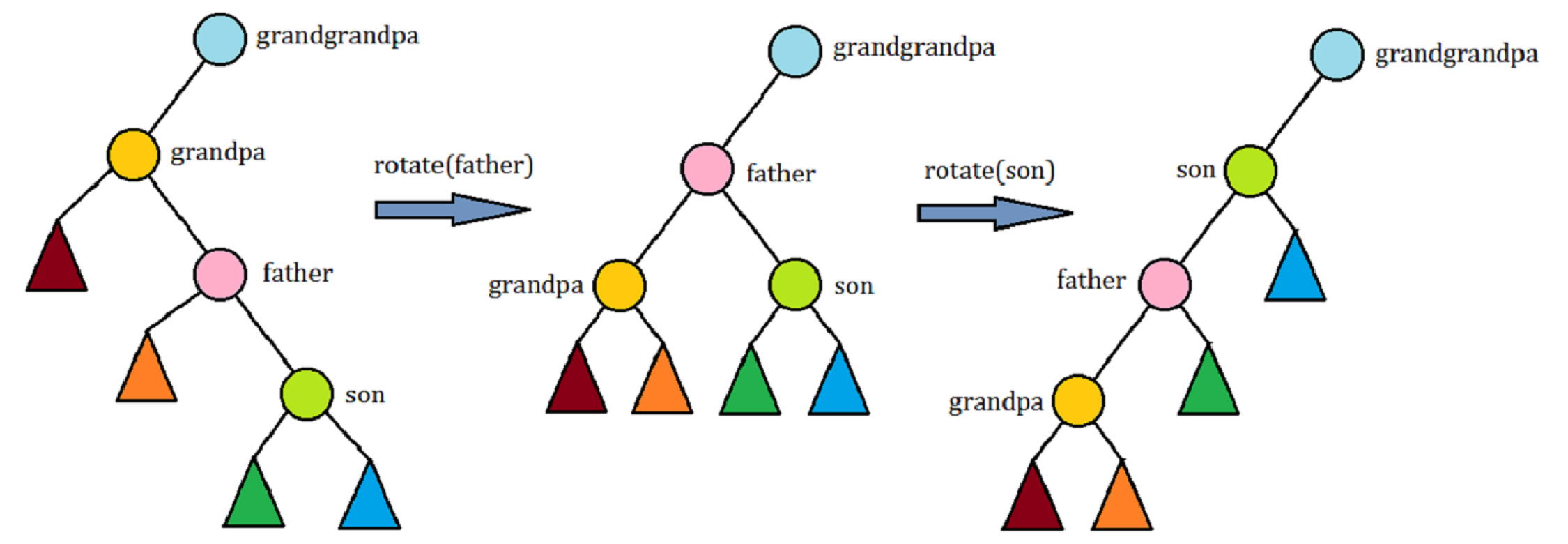
\(2.\) 当节点\(p\)的两代祖先不与其位于同一条链上时，直接两次旋转\(p\)即可.

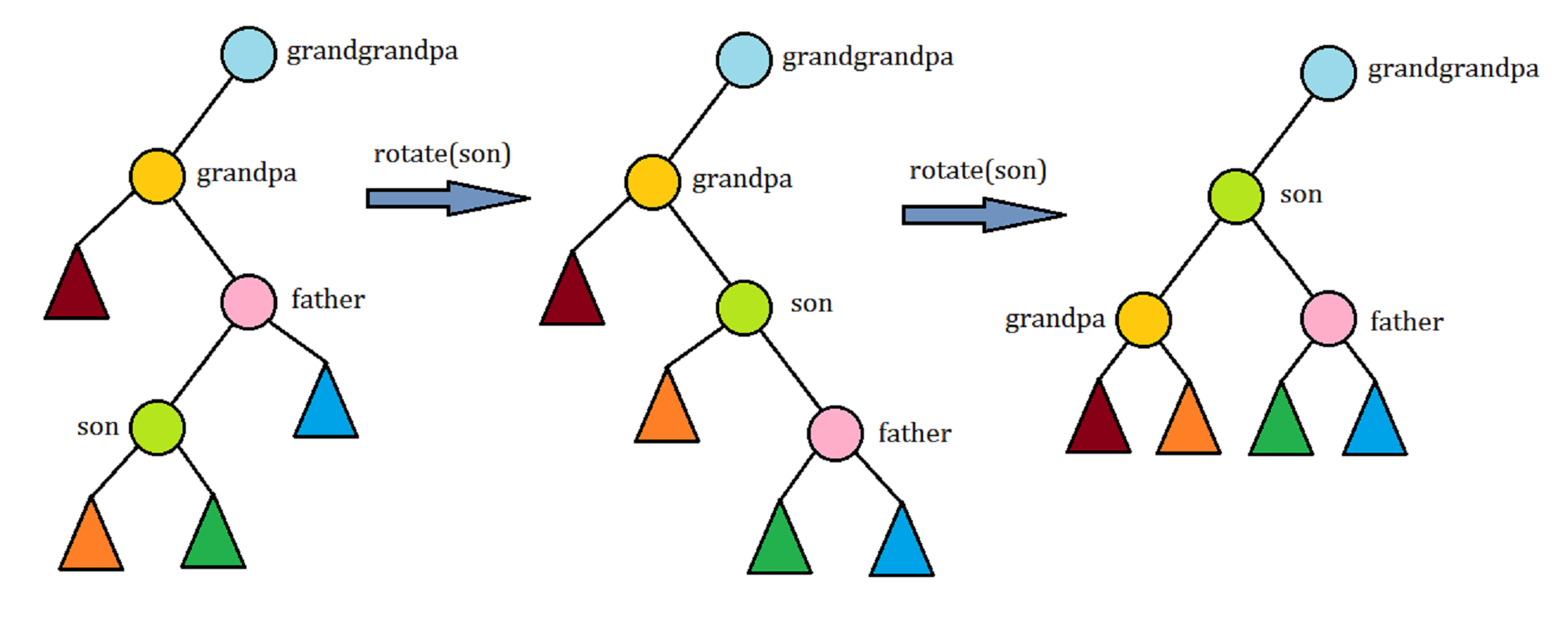
旋转的目的是让节点\(p\)的深度变浅，而采用双旋的方式是为了保证时间复杂度，在下一节会详细讲.

Splay

\(\mathrm{Splay}\)的核心操作是每一次把一个节点旋转到根，也就是伸展操作.

在双旋的基础上，伸展操作的实现很简单，当\(x\)是根节点的儿子时，直接单旋，否则分两组情况不断双旋即可.

时间复杂度

势能分析法

在分析\(\mathrm{Splay}\)的时间复杂度前，我们首先要知道势能分析法的原理.

首先，我们可以假设总共有\(m\)次操作，每次操作的实际消耗时间\(t_i\)难以估计，那么我们可以引入一个势能\(\Phi_i\)表示第\(i\)次操作完后的某个特征值，然后用\(a_i=t_i+\Delta\Phi=t_i+\Phi_i-\Phi_{i-1}\)表示第\(i\)次操作的均摊时间，那么有：

\[\sum_{i=1}^m t_i=\sum_{i=1}^m(a_i-\Delta \Phi)=\sum_{i=1}^m a_i+\Phi_0-\Phi_m \]

那么就可以通过分析\(\sum_{i=1}^m a_i+\Phi_0-\Phi_m\)的大小来分析\(m\)次操作的总时间.

时间复杂度证明

我们不妨令每个点势能函数\(\phi(x)=\log s(x)\)，整个\(\mathrm{Splay}\)的势能\(\Phi=\sum\phi(x)\). 根据均摊时间的定义，有\(a_i=t_i+\Delta\Phi\).

可以证明，均摊时间\(a_i\)满足\(a_i\leq 3(\phi'(x)-\phi(x))+1\)，其中\(x\)表示所操作的点的编号，\(\phi'\)表示这次操作完之后的势能函数.

那么总时间\(\sum_{i=1}^m t_i=\sum_{i=1}^m a_i+\Phi_0-\Phi_m\)，因为\(a_i\leq 3(\phi'(x)-\phi(x))+1\leq \log\frac{n}{s(x)}\leq \log n\)，\(\forall i\in[1,m]\)，\(\Phi\in[0,n\log n]\)，所以总时间不超过\(\mathcal{O}((n+m)\log n)\).

也就是说，我们的主要思路就是证明均摊复杂度\(a_i\)是\(\mathcal{O}(\log n)\)级别的，那么剩下的时间复杂度只要根据势能法的定义计算一下就好了.

均摊复杂度证明

现在我们要证明\(a_i\leq 3(\phi'(x)-\phi(x))+1\)，分三种情况讨论：

\(1.\) 节点\(x\)是根的直接儿子，单旋一次的均摊复杂度（图中的\(p\)就是此处的\(x\)）.

如图，\(a_i=1+\phi'(p)+\phi'(q)-\phi(p)-\phi(q)=1+\phi'(q)-\phi(p)\leq\phi'(p)-\phi(p)+1\)，原不等式成立.

\(2.\) 当节点\(x\)的两代祖先都与其位于同一条链上时，第一类双旋一次的均摊复杂度.

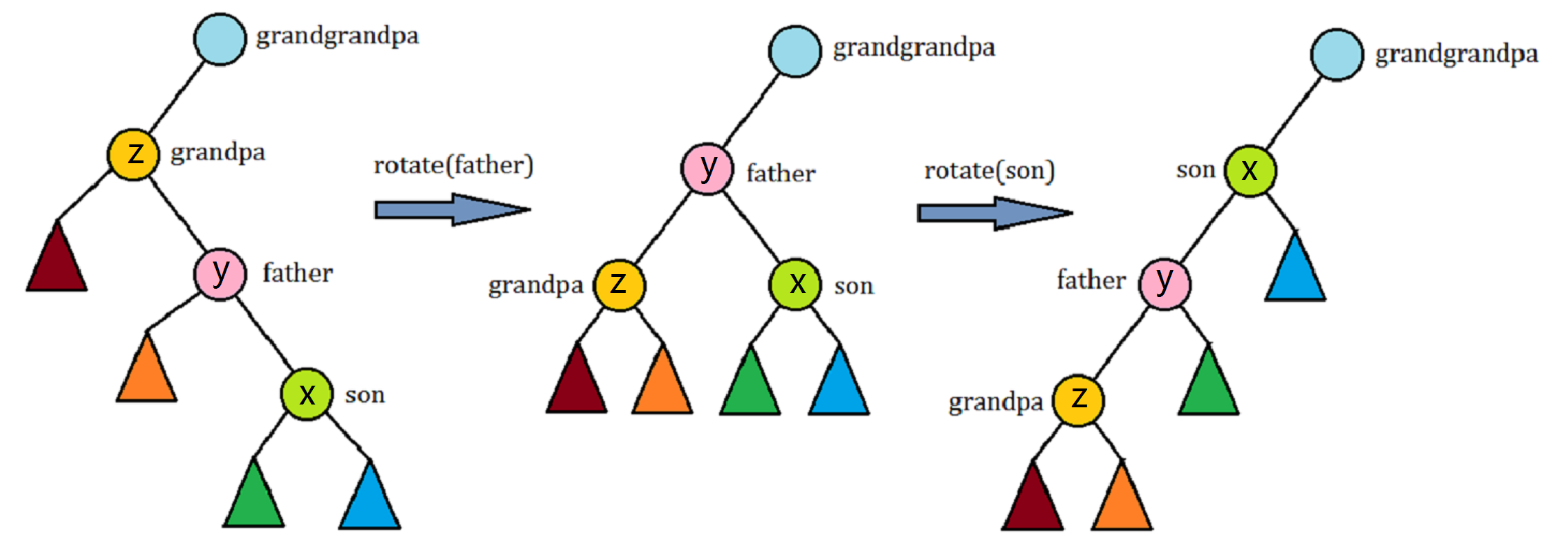
如图，有\(a_i=2+\phi'(x)+\phi'(y)+\phi'(x)-\phi(x)-\phi(y)-\phi(z)\)，由于\(\phi(z)=\phi'(x)\)，所以\(a_i=2+\phi'(y)+\phi'(z)-\phi(y)-\phi(x)\)，由于\(s(y)>s(x)\)，\(s'(x)>s'(y)\)，所以原式可以写作：

\[a_i=2+\phi'(y)+\phi'(z)-\phi(y)-\phi(x)<2+\phi'(x)+\phi'(z)-2\phi(x) \]

由于双旋操作可能有很多次，所以我们要设法将\(2+\phi'(x)+\phi'(z)-2\phi(x)\)转化为关于\(\phi'(x)-\phi(x)\)的形式，并且要把常数\(2\)给隐藏掉，否则时间复杂度难以分析.

不妨考虑式子\(\phi(x)+\phi'(z)-2\phi'(x)\)，由于\(s(x)+s'(z)<s'(x)\)，结合对数函数的性质:

\[\phi(x)+\phi'(z)-2\phi'(x)<\log \left( \frac{s(x)s'(z)}{(s(x)+s'(z))^2} \right)\leq \log\left(\frac{s(x)s'(z)}{2s(x)s'(z)}\right)=\log\frac{1}{2} \]

综上，就有：

\[\begin{cases}\log \frac{1}{2}-(\phi(x)+\phi'(z)-2\phi'(x))>0\\ a_i<2+\phi'(x)+\phi'(z)-2\phi(x)\end{cases} \]

两式相加得到：\(a_i<3(\phi'(x)-\phi(x))+2+\log\frac{1}{2}\).

值得注意的是，双旋操作有很多次，现在我们每次双旋的均摊时间肯定不能保留常数项，那么就要令\(2=\log 2\)，也就是说\(\log\)是以\(\sqrt 2\)为底的，这样常数项抵消，即使差分逐次累加，原不等式也成立了.

这里我们直接把一次旋转的时间看做\(1\)，但事实上可能还有一些常数，所以真正时间复杂度中\(\log\)的底数可能还要更小，这大概就是\(\mathrm{Splay}\)常数大的原因：我们不能简单的把\(\log\)看做\(\log_2\).

\(3.\) 当节点\(x\)的两代祖先不与其位于同一条链上时，第二类双旋一次的均摊复杂度.

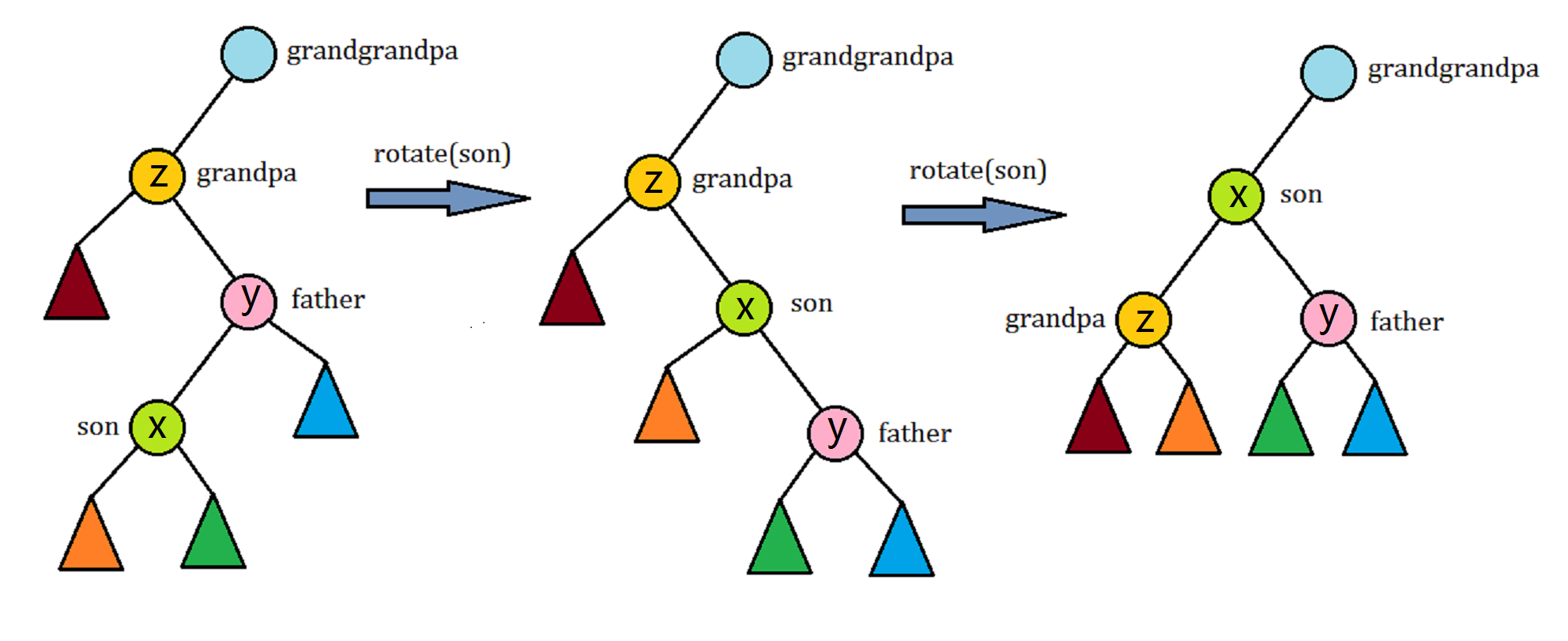
第一步是一样的，因为\(\phi(z)=\phi'(x),\phi(y)>\phi(x)\)，显然可以放缩为\(a_i<2+\phi'(z)+\phi'(y)-2\phi(x)\).

为了使其变成关于\(\phi(x)\)的差分，对应的式子就是\(\phi'(z)+\phi'(y)-2\phi'(x)\)，现在我们根据\(s'(x)>s'(y)+s'(z)\)，就有\(\phi'(z)+\phi'(y)-2\phi'(x)<\log\frac{1}{2}\)，也就是\(\log\frac{1}{2}-(\phi'(z)+\phi'(y)-2\phi'(x))>0\)，把两式相加就可以得到结论：

\[a_i<2(\phi'(x)-\phi(x))+2+\log\frac{1}{2}<3(\phi'(x)-\phi(x)) \]

显然，即使有多次双旋，差分会相互抵消，原不等式也成立.

\(\mathrm{Conclusion}:\) 通过对三种旋转的讨论，得出\(\mathrm{Splay}\)操作的均摊时间是\(\mathcal{O}(\log n)\)级别的. 因为\(\mathrm{BST}\)上的暴力操作时间复杂度与\(\mathrm{Splay}\)操作的时间复杂度消耗同阶，所以\(n\)个点，\(m\)次操作的\(\mathrm{Splay}\)的总时间消耗不超过\(\mathcal{O}((n+m)\log n)\).

优势分析

首先\(\mathrm{Splay}\)是常见的真平衡树的一种（还有另外两种是\(\mathrm{Split\ Merge\ Treap}\)和\(\mathrm{Weight\ Balanced\ Leafy\ Tree}\)），是可以提取区间的，也就是说，区间翻转之类的操作都可以实现.

其次，\(\mathrm{Splay}\)是\(\mathrm{Dynamic\ Finger\ Search\ Tree}\)，把\(n\)个点用\(\mathrm{Splay}\)启发式合并（拆解后从小到大加入到另一棵\(\mathrm{Splay}\)）的时间复杂度是\(\mathcal{O}(n\log n)\)的.

并且，\(\mathrm{Splay}\)通常用于实现\(\mathrm{Link-Cut\ Tree}\)，由于其时间复杂度的势能分析仍成立，所以时间复杂度是\(\mathrm{O}((n+m)\log n)\).

缺点：时间复杂度比较劣（\(\log\)不是以\(2\)为底，可能比较大），代码实现较长. 所以\(\mathrm{Splay}\)一般在实现\(\mathrm{LCT}\)时迫不得已才用，这里就不详细讲代码实现了，总结\(\mathrm{LCT}\)时会有代码.

Split Merge Treap

定义

非旋转\(\mathrm{Treap}\)，又称\(\mathrm{fhq-Treap}\)，利用分裂和合并来维护经典的随机平衡树\(\mathrm{Treap}\).

\(\mathrm{Treap}\)的原理很简单，对于树上的每一个点\(p\)，我们都给它一个额外的随机权值\(\mathrm{ext}(p)\)，并保证\(\mathrm{Treap}\)是一棵关键字为\((\mathrm{val}(p),\mathrm{ext}(p))\)的笛卡尔树，那么这样的\(\mathrm{BST}\)的期望树高就是\(\mathcal{O}(\log_2 n)\)的，从而保证所有操作的单次时间复杂度都是期望\(\mathcal{O}(\log_2 n)\)的.

具体来说，\(\mathrm{Treap}\)的结构其实相当于一个最终大小关系确定的序列（即中序遍历确定），那么每一次随便找一个点为根，左右两边递归就相当于随机取点的快速排序，期望复杂度就是\(\mathrm{O}(n\log_2n)\).

实现\(\mathrm{Treap}\)的关键在于如何维护笛卡尔树的形态，一种方法是旋转，但是具有较大的局限性，更好的方法是分裂和合并. 事实上，\(\mathrm{SMT}\)的代码实现是最简单的，实用性很强，接下来终点讲实现.

实现

Split

\(\mathrm{Split}\)操作指的是将一棵\(\mathrm{BST}\)分为两棵，可以按照权值分，也可以按照大小分. 按照权值分指的是将树\(\mathrm{T}\)分为\(\mathrm{T_1,T_2}\)两棵树，其中\(\mathrm{T_1}\)包括了\(\mathrm{T}\)中所有权值小于等于\(v\)的点，\(\mathrm{T_2}\)包括了剩下的点. 按大小分也是同理，\(\mathrm{T_1}\)包括了\(\mathrm{T}\)中权值最小的\(k\)个点，\(\mathrm{T_2}\)包括了剩下的点.

代码实现很简单，只要直接递归分裂即可.

inline void Splitv(int p,int v,int &a,int &b) {
    if ( !p ) return a = b = 0 , void(); return val(p) <= v ?
    ( a = p , Splitv(rs(p),v,rs(p),b) , Update(p) ) : ( b = p , Splitv(ls(p),v,a,ls(p)) , Update(p) );
}
inline void Splitk(int p,int k,int &a,int &b) {
    if ( !p ) return a = b = 0 , void(); int rk = k - cnt(ls(p)) - 1 , lk = k; return cnt(ls(p)) < k ?
    ( a = p , Splitk(rs(p),rk,rs(p),b) , Update(p) ) : ( b = p , Splitk(ls(p),lk,a,ls(p)) , Update(p) );
}

Merge

\(\mathrm{Merge}\)就是\(\mathrm{Split}\)的逆过程，可以合并两棵树，但是必须要求第一棵树的最大权小于第二棵树的最小权，也就是必须要有绝对的大小关系，不然是不能直接递归合并的，要启发式合并.

当然，在\(\mathrm{Merge}\)的时候显然我们要关注那个节点作为父节点的问题，这个就由\(\mathrm{Treap}\)的随机性能决定，也就是说我们要顺带维护\(\mathrm{Treap}\)的堆性质，这样的话就可以递归了.

inline int Merge(int a,int b) {
    if ( !a || !b ) return a | b; return ext(a) < ext(b) ?
    ( rs(a) = Merge(rs(a),b) , Update(a) , a ) : ( ls(b) = Merge(a,ls(b)) , Update(b) , b );
}

Insert

假如我们要插入数字\(v\)，只要把原树分为两半，一边小于等于\(v\)，一边大于\(v\)，把新点看做一棵大小为\(1\)的树，然后\(\mathrm{Merge}\)两次即可.

inline void Insert(int v) { Splitv(rt,v,x,y) , rt = Merge( Merge(x,Creat(v)) , y ); }

Remove

道理和\(\mathrm{Insert}\)差不多，先把树分成三部分，小于\(v\)的，等于\(v\)的和大于\(v\)的树，那么只要把等于\(v\)的那棵树中的根节点删掉就好了，方法是合并左右儿子.

inline void Remove(int v) { Splitv(rt,v,x,z) , Splitv(x,v-1,x,y) , y = Merge(ls(y),rs(y)) , rt = Merge(x,Merge(y,z)); }

Select

将前\(k\)小的数字放在一起，然后从根节点一直往右走找到最大的那个数值即可.

inline int Select(int k) { Splitk(rt,k,x,y); for (z=x;rs(z);z=rs(z)); return rt = Merge(x,y) , val(z); }

Rank

把权值小于等于\(v-1\)的数字放在树\(\mathrm{T'}\)里，只要返回\(\mathrm{|T'|+1}\)即可.

inline int Rank(int v) { Splitv(rt,v-1,x,y) , z = cnt(x) + 1; return rt = Merge(x,y) , z; }

Range

假如把\(\mathrm{Treap}\)建成区间树的话就可以提取区间，只需要把树分成\([1,l-1],[l,r],[r+1,n]\)三部分，对中间那棵子树做想做的操作就好了.

inline void Range(int l,int r) { Splitk(rt,r,x,z) , Splitk(x,l-1,x,y) , Apply(y) , rt = Merge(Merge(x,y),z); }

优势分析

\(\mathrm{Split\ Merge\ Treap}\)应该是性价比最高的平衡树，主要优势在于容易实现，代码简单，并且可以作为区间树使用.

由于其维护\(\mathrm{BST}\)的原理是分裂合并，所以还可以支持可持久化.

相比较于\(\mathrm{Splay}\)而言的话，缺点就是实现启发式合并和\(\mathrm{LCT}\)都只能\(O(n\log^2n)\)，常数不算太好，但是比\(\mathrm{Splay}\)还是要快一些，应付一般的平衡树题没有什么问题.

Epilogue