网络流24题（十六）

网络流24题(十六)

十六、数字梯形问题

题目描述

给定一个由 n 行数字组成的数字梯形如下图所示。

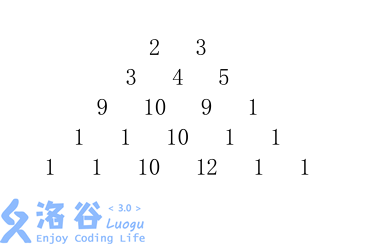
梯形的第一行有 m 个数字。从梯形的顶部的 m 个数字开始，在每个数字处可以沿左下或右下方向移动，形成一条从梯形的顶至底的路径。

分别遵守以下规则：

从梯形的顶至底的 m 条路径互不相交；
从梯形的顶至底的 m 条路径仅在数字结点处相交；
从梯形的顶至底的 m 条路径允许在数字结点相交或边相交。

输入格式

第 1 行中有 2 个正整数 m 和 n，分别表示数字梯形的第一行有 m 个数字，共有 n 行。接下来的 n 行是数字梯形中各行的数字。

第 1 行有 m 个数字，第 2 行有 m+1个数字，以此类推。

输出格式

将按照规则 1，规则 2，和规则 3 计算出的最大数字总和并输出，每行一个最大总和。

题解

模型

最大费用最大流，然后还需要考虑拆点维护点的流量。
三个问题都可以拆点维护点的流量，虽然问题二三不拆点也可以过（问题三dp都可以）。

建图

问题一：
把梯形中每个位置抽象为两个点<i.a>,<i.b>，建立附加源S汇T。

对于每个点i从<i.a>到<i.b>连接一条容量为1，费用为点i权值的有向边。
从S向梯形顶层每个<i.a>连一条容量为1，费用为0的有向边。
从梯形底层每个<i.b>向T连一条容量为1，费用为0的有向边。
对于每个点i和下面的两个点j，分别连一条从<i.b>到<j.a>容量为1，费用为0的有向边。

求最大费用最大流，费用流值就是结果。

问题二：
将上面流量限制变为无穷即可，或者干脆不拆点，\(u\)->\(v\)的权值就是点\(u\)的值。跑最大费用最大流就好了。

问题三：
同上

代码

全拆点写法

#include <iostream>
#include <queue>
#include <stack>
#include <map>
#include <cstring>
using namespace std;
#define ll long long
const ll inf = 0x3f3f3f3f;
const int N = 5000,M = 5e4+50;
ll head[N],cnt = 1;
struct Edge{
    ll to,w,cost,nxt;
}edge[M*2];
void add(ll u,ll v,ll w,ll c){
    edge[++cnt] = {v,w,c,head[u]};
    head[u] = cnt;
}
void add2(ll u,ll v,ll w,ll cost){
    add(u,v,w,cost);
    add(v,u,0,-cost);
}
ll s,t,dis[N],cur[N];
bool inq[N],vis[N];
queue<ll>Q;
bool spfa(){
    while(!Q.empty()) Q.pop();
    copy(head,head+N,cur);
    fill(dis,dis+N,inf);
    dis[s] = 0;
    Q.push(s);
    while(!Q.empty()){
        ll p = Q.front();
        Q.pop();
        inq[p] = false;
        for(ll e = head[p];e;e = edge[e].nxt){
            ll to = edge[e].to,vol = edge[e].w;
            if(vol > 0 && dis[to]>dis[p]+edge[e].cost){
                dis[to] = dis[p] + edge[e].cost;
                if(!inq[to]){
                    Q.push(to);
                    inq[to] = true;
                }
            }
        }
    }
    return dis[t] != inf;
}
ll dfs(ll p = s,ll flow = inf){
    if(p == t) return flow;
    vis[p] = true;
    ll rmn = flow;
    for(ll eg = cur[p];eg && rmn;eg = edge[eg].nxt){
        cur[p] = eg;
        ll to = edge[eg].to,vol = edge[eg].w;
        if(vol > 0 && !vis[to]&&dis[to] == dis[p]+edge[eg].cost){
            ll c = dfs(to,min(vol,rmn));
            rmn -= c;
            edge[eg].w -= c;
            edge[eg^1].w += c;
        }
    }
    vis[p] = false;
    return flow-rmn;
}
ll maxflow,mincost;
void dinic(){
    maxflow = 0,mincost = 0;
    while(spfa()){
        ll flow = dfs();
        maxflow += flow;
        mincost += dis[t]*flow;
    }
}
ll ma[N][N],cnt0 = 0,n,m;
map<pair<ll,ll>,ll > com;
void q1(){
    memset(head,0,sizeof head);
    cnt = 1;
    for(ll i = 1;i <= m;i++){
        add2(2*cnt0+2,com[{1,i}],1,0);
    }
    for(ll i = 1;i <= n;i++){
        for(ll j = 1;j <= m+i-1;j++){
            if(i != n) {
                add2(com[{i, j}]+cnt0, com[{i + 1, j}], 1, 0);
                add2(com[{i, j}]+cnt0, com[{i + 1, j + 1}], 1, 0);
            }else{
                add2(com[{i, j}]+cnt0,2*cnt0+1,1,0);
            }
            add2(com[{i,j}],com[{i,j}]+cnt0,1,-ma[i][j]);
        }
    }
    s = 2*cnt0+3,t = 2*cnt0+4;
    add2(s,2*cnt0+2,m,0);add2(2*cnt0+1,t,m,0);
    dinic();
    cout<<-mincost<<endl;
}
void q2(){
    memset(head,0,sizeof head);
    cnt = 1;
    s = 2*cnt0+3,t = 2*cnt0+4;
    for(ll i = 1;i <= m;i++){
        add2(s,com[{1,i}],1,0);
    }
    
    for(ll i = 1;i <= n;i++){
        for(ll j = 1;j <= m+i-1;j++){
            if(i != n) {
                add2(com[{i, j}]+cnt0, com[{i + 1, j}], 1, 0);
                add2(com[{i, j}]+cnt0, com[{i + 1, j + 1}], 1, 0);
            }else{
                add2(com[{i, j}]+cnt0,t,inf,0);
            }
            add2(com[{i,j}],com[{i,j}]+cnt0,inf,-ma[i][j]);
        }
    }
    dinic();
    cout<<-mincost<<endl;
}
void q3(){
    memset(head,0,sizeof head);
    cnt = 1;
    s = 2*cnt0+3,t = 2*cnt0+4;
    for(ll i = 1;i <= m;i++){
        add2(s,com[{1,i}],1,0);
    }
    for(ll i = 1;i <= n;i++){
        for(ll j = 1;j <= m+i-1;j++){
            if(i != n) {
                add2(com[{i, j}]+cnt0, com[{i + 1, j}], inf, 0);
                add2(com[{i, j}]+cnt0, com[{i + 1, j + 1}], inf, 0);
            }else{
                add2(com[{i, j}]+cnt0,t,inf,0);
            }
            add2(com[{i,j}],com[{i,j}]+cnt0,inf,-ma[i][j]);
        }
    }
    dinic();
    cout<<-mincost<<endl;
}
int main(){
    //ios::sync_with_stdio(false);
    cin>>m>>n;
    for(ll i = 1;i <= n;i++){
        for(ll j = 1;j <= m+i-1;j++){
            cin>>ma[i][j];
            com[{i,j}] = ++cnt0;
        }
    }
    q1();q2();q3();
    return 0;
}

不拆点写法：

#include <iostream>
#include <queue>
#include <stack>
#include <map>
#include <cstring>
using namespace std;
#define ll long long
const ll inf = 0x3f3f3f3f;
const int N = 5000,M = 5e4+50;
ll head[N],cnt = 1;
struct Edge{
    ll to,w,cost,nxt;
}edge[M*2];
void add(ll u,ll v,ll w,ll c){
    edge[++cnt] = {v,w,c,head[u]};
    head[u] = cnt;
}
void add2(ll u,ll v,ll w,ll cost){
    add(u,v,w,cost);
    add(v,u,0,-cost);
}
ll s,t,dis[N],cur[N];
bool inq[N],vis[N];
queue<ll>Q;
bool spfa(){
    while(!Q.empty()) Q.pop();
    copy(head,head+N,cur);
    fill(dis,dis+N,inf);
    dis[s] = 0;
    Q.push(s);
    while(!Q.empty()){
        ll p = Q.front();
        Q.pop();
        inq[p] = false;
        for(ll e = head[p];e;e = edge[e].nxt){
            ll to = edge[e].to,vol = edge[e].w;
            if(vol > 0 && dis[to]>dis[p]+edge[e].cost){
                dis[to] = dis[p] + edge[e].cost;
                if(!inq[to]){
                    Q.push(to);
                    inq[to] = true;
                }
            }
        }
    }
    return dis[t] != inf;
}
ll dfs(ll p = s,ll flow = inf){
    if(p == t) return flow;
    vis[p] = true;
    ll rmn = flow;
    for(ll eg = cur[p];eg && rmn;eg = edge[eg].nxt){
        cur[p] = eg;
        ll to = edge[eg].to,vol = edge[eg].w;
        if(vol > 0 && !vis[to]&&dis[to] == dis[p]+edge[eg].cost){
            ll c = dfs(to,min(vol,rmn));
            rmn -= c;
            edge[eg].w -= c;
            edge[eg^1].w += c;
        }
    }
    vis[p] = false;
    return flow-rmn;
}
ll maxflow,mincost;
void dinic(){
    maxflow = 0,mincost = 0;
    while(spfa()){
        ll flow = dfs();
        maxflow += flow;
        mincost += dis[t]*flow;
    }
}
ll ma[N][N],cnt0 = 0,n,m;
map<pair<ll,ll>,ll > com;
void q1(){
    memset(head,0,sizeof head);
    cnt = 1;
    for(ll i = 1;i <= m;i++){
        add2(2*cnt0+2,com[{1,i}],1,0);
    }
    for(ll i = 1;i <= n;i++){
        for(ll j = 1;j <= m+i-1;j++){
            if(i != n) {
                add2(com[{i, j}]+cnt0, com[{i + 1, j}], 1, 0);
                add2(com[{i, j}]+cnt0, com[{i + 1, j + 1}], 1, 0);
            }else{
                add2(com[{i, j}]+cnt0,2*cnt0+1,1,0);
            }
            add2(com[{i,j}],com[{i,j}]+cnt0,1,-ma[i][j]);
        }
    }
    s = 2*cnt0+3,t = 2*cnt0+4;
    add2(s,2*cnt0+2,m,0);add2(2*cnt0+1,t,m,0);
    dinic();
    cout<<-mincost<<endl;
}
void q2(){
    memset(head,0,sizeof head);
    cnt = 1;
    s = 0,t = cnt0+1;
    for(ll i = 1;i <= m;i++){
        add2(s,com[{1,i}],1,0);
    }
    for(ll i = 1;i <= n;i++){
        for(ll j = 1;j <= m+i-1;j++){
            if(i != n) {
                add2(com[{i, j}], com[{i + 1, j}], 1, -ma[i][j]);
                add2(com[{i, j}], com[{i + 1, j + 1}], 1, -ma[i][j]);
            }else{
                add2(com[{i, j}],t,inf,-ma[i][j]);
            }
        }
    }
    dinic();
    cout<<-mincost<<endl;
}
void q3(){
    memset(head,0,sizeof head);
    cnt = 1;
    s = 0,t = cnt0+1;
    for(ll i = 1;i <= m;i++){
        add2(s,com[{1,i}],1,0);
    }
    for(ll i = 1;i <= n;i++){
        for(ll j = 1;j <= m+i-1;j++){
            if(i != n) {
                add2(com[{i, j}], com[{i + 1, j}], inf, -ma[i][j]);
                add2(com[{i, j}], com[{i + 1, j + 1}], inf, -ma[i][j]);
            }else{
                add2(com[{i, j}],t,inf,-ma[i][j]);
            }
        }
    }
    dinic();
    cout<<-mincost<<endl;
}
int main(){
    //ios::sync_with_stdio(false);
    cin>>m>>n;
    for(ll i = 1;i <= n;i++){
        for(ll j = 1;j <= m+i-1;j++){
            cin>>ma[i][j];
            com[{i,j}] = ++cnt0;
        }
    }
    q1();q2();q3();
    return 0;
}

posted @ 2021-10-26 12:33 Paranoid5 阅读(51) 评论(0) 收藏举报

刷新页面返回顶部

Paranoid

我这才明白，我从未真正见过火，也未见过毁灭，更不知新生。