主成分分析PCA算法笔记

导论

　　当自变量X₁和X₂分别为（1,2,4,5,15），（1,2,4,5,15）时，对应因变量Y有相应的取值（7,8,9,14,55）；这里的数据随便取的，但是我们发现X₁和X₂有个线性关系；甚至我们可以生成一个X₃坐标轴，以45度夹在X₁轴和X₂轴之间，以代替X₁轴和X₂轴来对应因变量Y，这便是将数据降维了，图示如下

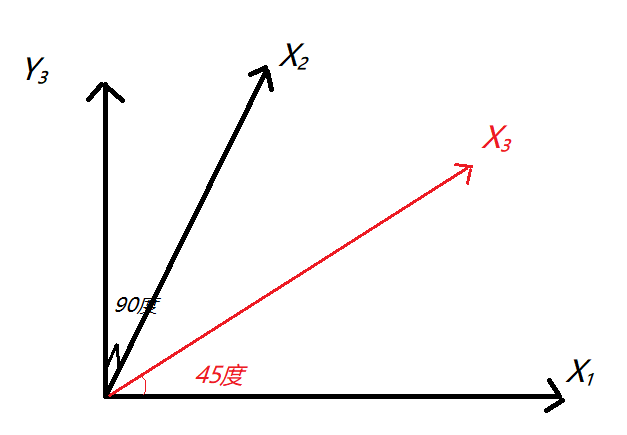
　　如果选取了X₃轴，发现数据在其轴的投影的方差变大了。俯视图如下：

 

 

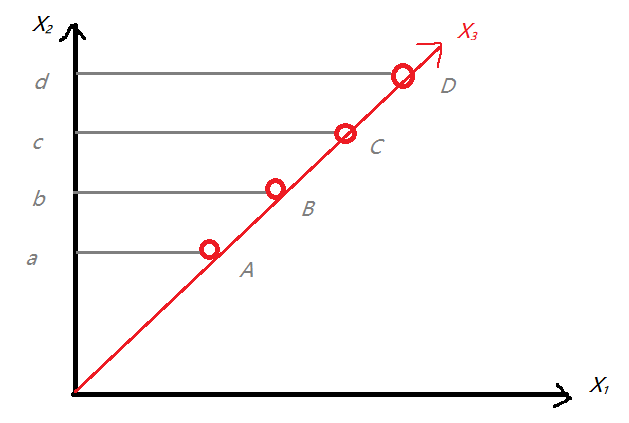
　　明显，a,b,c,d之间的方差小于A,B,C,D之间的方差，而且恰恰X₃轴能更好地拟合这条直线。

　　似乎信号论有什么：方差大的方向是数据方向，方差小的方向是噪声方向；于是我们应该在PCA分析中首先将方差大的方向依次进行保留，方差最小的那么几个可以舍去；

求特征值与特征向量

　　于是主成分分析的任务在于将原来的坐标轴进行旋转，使其到达数据投影方差最大的几个轴；

首先采集n维因变量的数据各m个,组成数据阵N：

 

 

 

 

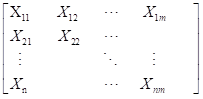
　　如果多维的因变量之间量纲不同，选取相关系数矩阵研究，由于

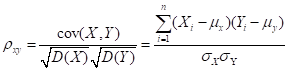
　　将数据阵N内的数据进行标准化处理（去量纲化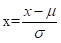）：，构成的矩阵称为设计阵A，那么相关系数矩阵可以表示为AA’

如果多维的因变量之间量纲相同，选取协方差矩阵研究，

标准化即为去中心化：，构成的矩阵称为设计阵A，那么协方差矩阵可以表示为AA'/(n-1)

至于有（n-1），是因为样本（协）方差的无偏估计要求的；

后续提到的x不是原数据，而是标准后数据

 

　　设相关系数矩阵（协方差矩阵）为C，C为实对称矩阵，那么它的特征向量注定正交；且可对角化为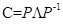：  ，P为特征向量的集合，中间的为特征值对角阵：

特征值等于方差

先抛出结论：相关系数矩阵（协方差矩阵）的特征值=数据在新坐标轴上的方差

　　首先作为特征向量矩阵P，是个正交矩阵，据说就是这个玩意把坐标轴旋转到了恰当的地步，达到PCA的要求；那么对于新数据向量z理应等于p乘以标准化的数据x，这样，新数据矩阵也理应各个正交，而没有协方差。它的协方差矩阵为对角阵，对角元素即为自方差；

 

 

 

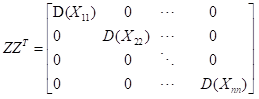
　　对于新数据协方差矩阵（省去n-1的运算，结论不变）：

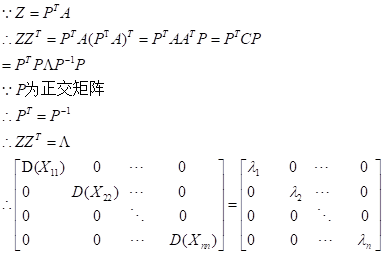
　　故此，相关系数矩阵（协方差矩阵）的特征值=数据在新坐标轴上的方差

 尾注

　　对于原先坐标轴，基系为单位矩阵E，就比如X₁轴向量为[1  0],X₂轴向量为[0  1],组合起来便为单位矩阵E；而对于任意向量V，在此空间的变换为E*V=V，也就是不变；

　　而对于变换后的坐标轴，比如对原基系E做旋转变换而成，旋转矩阵为正交矩阵P，此空间的基系便为E*P=P，原向量V在此空间产生变换，为P*V，原向量在此空间形式便为向量P*V。