数据结构之树
树(tree)
一、定义
树是n个节点的有限集。n=0时称为空树,n>1时其余结点可分为m(m>0)个互不相交的有限集,其中每个集合本身又是一棵树,并且称为根的子树。形状类似于树状图,如下图所示:
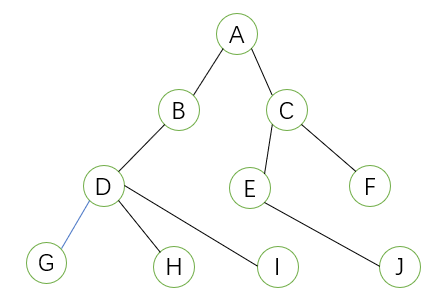
再次强调几点:
1.根节点是唯一的,不可能存在多个根节点。
2.子树的个数没有限制,但是一定不可能相互相交,比如上图中D和E不能相连,E和I不能相连。
3. 子树的概念对每个节点都适用,即递归的方法,这也是程序实现的关键点。
二、专业术语
度:节点的子树数,树的度是所有节点里度最大的节点的度。
叶节点(终端节点):度为0的节点
分支节点(非终端节点):度不为0的节点
树的深度:树中节点的最大层次,如上图就为4层。
孩子、双亲、堂兄弟、子孙、祖先:不解释,和认知相同。
三、树的存储结构
关键:将树这种非线性结构转换为线性结构存储在计算机内部,
即用数组的下标进行保存,注意根节点下标为0开始,如双亲表示法。
也可以用链表保存,如孩子表示法。
(1)双亲表示法:
为什么取名为双亲表示法?因为刚开始的时候一个节点仅仅只是保存了数据和该节点的双亲的下标(根节点双亲下标为-1)。如:
![]()
但是我们还想要知道该节点的孩子有哪些、兄弟有哪些怎么办?对于只有至多两个孩子和至多一个兄弟的节点,我们可以加上左孩子的坐标(无孩子存-1)和右兄弟的坐标(无兄弟存-1),因为知道了一个孩子就知道了另外一个孩子了,如:

程序可以为如下:
#define MAX_TREE_SIZE 100 //节点最大个数 struct Node { int data; int parent; int Lchild; int Rbro; }; struct Tree { struct Node node[MAX_TREE_SIZE]; int r,n; //节点的坐标和节点的个数 };
(2)孩子表示法
为什么取名为孩子表示法?因为刚开始的时候每个节点只是保存了数据和孩子的地址而已,节点如下图所示:
![]()
但是这也只是知道它的孩子的位置而已,我们还需要知道该节点的双亲、兄弟呀,怎么办?我们采用第一种方式改良版,即一个节点内存储有数据、双亲的下标和第一个孩子的地址(无孩子指针域为NULL),如下:

而第一个孩子节点存储孩子的下标和下一个孩子的地址,依次类推多个孩子。如:

程序如下:
#define MAX_TREE_SIZE 100 //节点最大个数 struct ChildNode { int child; struct ChildNode *next; }; struct Node { int data; int parent; struct ChildNode firstchild; }; struct Tree { struct Node node[MAX_TREE_SIZE]; int r,n; //节点的坐标和节点的个数 };
(3)孩子兄弟表示法
同上,之所这么命名是因为节点存储内容不仅仅包括了数据,还有第一个孩子的地址和该节点右边第一个兄弟的地址,如:

程序如下:
struct Node { int data; struct Node *firstChild,*rightbro; };
这种方法最大的优点:将任意树转换为二叉树存储,后面将转换为二叉树还会详细介绍。
四、树的分类
一般树:节点的子树数目无要求。
二叉树:每个节点的子树数目至多为两个。
森林:多颗树的集合,注意这些树没有连在一起。
五、树的存储结构(二叉树的最重要)
(1)二叉树
1.有三类特殊的二叉树形式。
- 斜树:所有节点只存在左子树或者只存在右子树,如下:
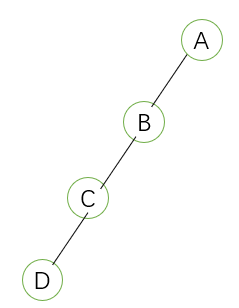
- 满二叉树:除最后一层,所有节点都存在两颗子树,如:
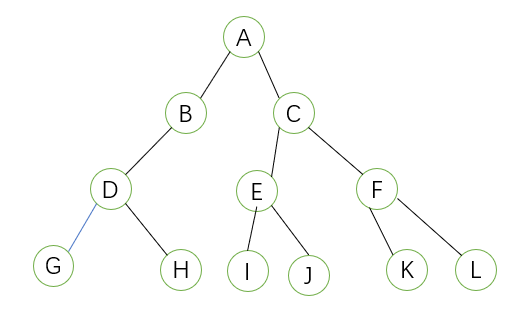
- 完全二叉树:用人话说,就是从最下面最右边开始往左边减少节点数目,然后往上移,如:
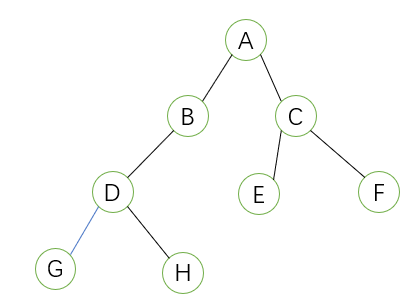
2. 二叉树的性质
- 在二叉树的第i层至多有2i-1节点。
- 深度为k的二叉树至多有2k-1个节点。
- 其余性质看书吧,和数学证明有关。
3. 二叉树的存储
使用了孩子表示法,即一个节点内部包含数据、左孩子的地址和有孩子的地址。
程序如下:
typedef struct BTNode { char data; struct BTNode *pLchild; struct BTNode *pRchild; }BTNODE,*PBTNODE;
4. 二叉树的遍历
- 二叉树连续存储的先序遍历操作(重点):
先访问根节点,再先序访问左子树,再先序访问右子树。
- 二叉树连续存储的中序遍历操作(重点):
中序遍历左子树,再访问根节点,再中序遍历右子树
- 二叉树连续存储的后序遍历操作(重点):
中序遍历左子树,中序遍历右子树,再访问根节点
- 只有已知两种遍历序列才可以求出原始二叉树:
通过先序和中序、或者中序和后序我们可以还原出原始的二叉树,但是通过先序和后序无法还原出原始的二叉树。当然,单靠一个更不可能还原出。
三种遍序(递归实现)程序如下:
#include<stdio.h> #include<malloc.h> PBTNODE CreateBTree(); void PreTraverseBTree(PBTNODE); void InraverseBTree(PBTNODE); void PostTraverseBtree(PBTNODE); int main() { PBTNODE pT; pT=CreateBTree(); PreTraverseBTree(pT);//先序遍历 printf("*********\n"); InraverseBTree(pT); printf("*********\n"); PostTraverseBtree(pT); return 0; } void PreTraverseBTree(PBTNODE pT) { /*用递归实现:先访问根节点,再先序访问左子树,再右子树*/ if(pT!=NULL) { printf("%c\n",pT->data); if(pT->pLchild!=NULL) PreTraverseBTree(pT->pLchild); if(pT->pRchild!=NULL) PreTraverseBTree(pT->pRchild); } return; } void InraverseBTree(PBTNODE pT) { if(pT!=NULL) { if(pT->pLchild!=NULL) PreTraverseBTree(pT->pLchild); printf("%c\n",pT->data); if(pT->pRchild!=NULL) PreTraverseBTree(pT->pRchild); } return; } void PostTraverseBtree(PBTNODE pT) { if(pT!=NULL) { if(pT->pLchild!=NULL) PreTraverseBTree(pT->pLchild); if(pT->pRchild!=NULL) PreTraverseBTree(pT->pRchild); printf("%c\n",pT->data); } return; } PBTNODE CreateBTree()//静态创建树 { PBTNODE pA=(PBTNODE)malloc(sizeof(BTNODE)); PBTNODE pB=(PBTNODE)malloc(sizeof(BTNODE)); PBTNODE pC=(PBTNODE)malloc(sizeof(BTNODE)); PBTNODE pD=(PBTNODE)malloc(sizeof(BTNODE)); PBTNODE pE=(PBTNODE)malloc(sizeof(BTNODE)); pA->data='A'; pB->data='B'; pC->data='C'; pD->data='D'; pE->data='E'; pA->pLchild=pB; pA->pRchild=pC; pB->pLchild=pB->pRchild=NULL; pC->pLchild=pD; pC->pRchild=NULL; pD->pLchild=NULL; pD->pRchild=pE; pE->pLchild=pE->pRchild=NULL; return pA; }
5. 二叉树的生成
比如我们想要输入下列二叉树:
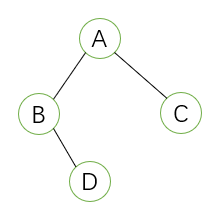
我们需要把它拓展如下,做一个标志标志该树输入完毕:
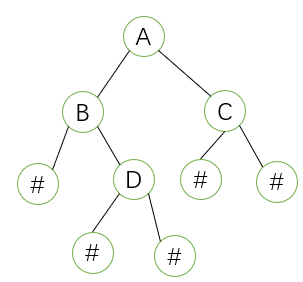
然后我们用前序遍历法输入数据,程序如下:
typedef struct BTNode { char data; struct BTNode *pLchild; struct BTNode *pRchild; }BTNODE,*PBTNODE; void CreateTree(PBTNODE T) { int ch; scanf("%c",&c); if(ch=='#') T=NULL; else { T=(PBTNODE)malloc(sizeof(BTNODE)); if(T==NULL) exit(-1); T->data=ch; CreateTree(T->pLchild); CreateTree(T->pRchild); } }
6. 线索二叉树
我们发现,当二叉树较多空指针的时候,如果用上面结构存储的话会比较浪费空间,比如下图:
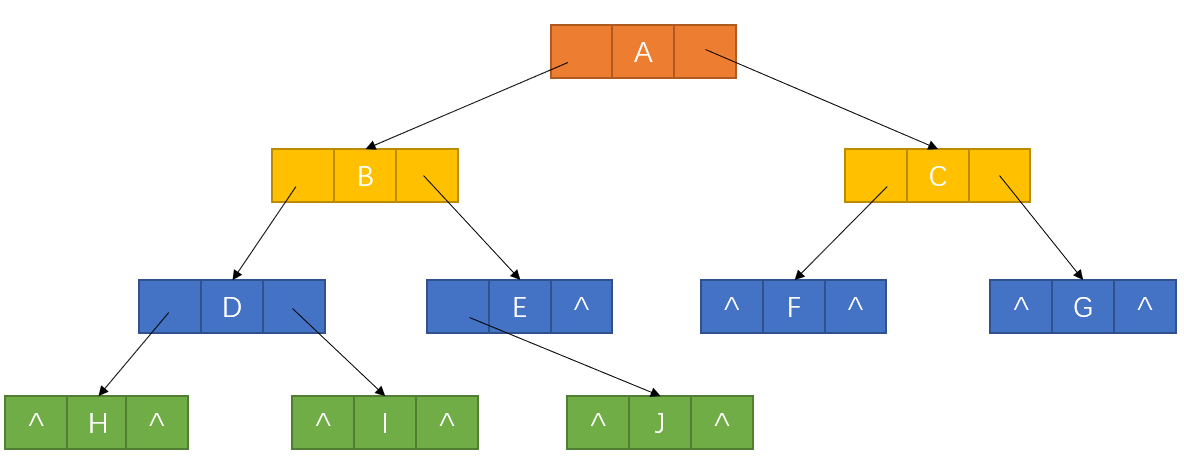
因此我们可以考虑利用这些空指针,存放指向节点在某种遍序操作下的前驱和后继节点的地址。指向前驱和后继的指针称为线索,加上线索的二叉树称为线索二叉树。
但是这样会导致我们不知道孩子指向的到底是下一个节点还是其前驱后驱,因此我们需要加标志位来帮助识别,因此一个节点存储的内容变为:
![]()
标志为0是指向孩子,为1是指向节点前驱,左边只能指向前驱节点,右边只能指向后驱节点。
以上图,中序遍历为例,可以改造成:
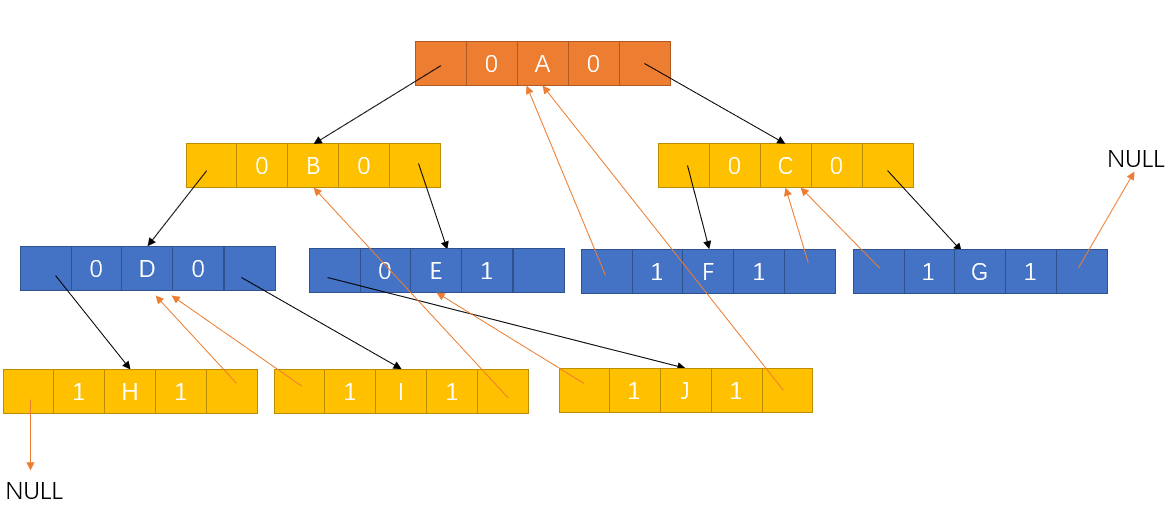
本质上也就是在各个节点之间创造了双向链而已。
线索二叉树的定义和中序遍历创造双向链的程序如下:
typedef enum {Link,Thread} PointerTag; //Link表示存放孩子,Thread表示存放前驱后驱 typedef struct Node { int data; struct Node *Lchild,*Rchild; PointerTag Ltag,Rtag; }NODE,*PNODE; PNODE *pre; void InThreading(PNODE p) { if(p) { InThreading(p->Lchild); if(!p->Lchild) { p->Ltag=Thread; p->Lchild=pre; } if(!pre->Rchild) { pre->Rtag=Thread;; pre->Rchild=p; } pre=p; InThreading(p->Rchild); } } //if(!p->Lchild)表示如果某节点的左指针域为空,因为其前驱节点刚刚访问过,赋值给pre,所以 //可以将pre赋值给p->Lchild,并修改p->Ltag为Thread以完成前驱节点的线索化。 //因为此时还没有访问到p节点的后驱节点,因此只能对它的前驱节点pre的右指针Rchild做判断,如 //果前驱的右指针为空,则p是pre的后继,于是pre->Rchild=p,完成后继节点的线索化。
既然是双向链表,我们可以用头指针操作来,让头结点左孩子指向根节点,有孩子指向中序遍历时访问的最后一个节点。反之,让访问的第一个节点左孩子指向和最后一个节点的右孩子均指向头结点,如下:
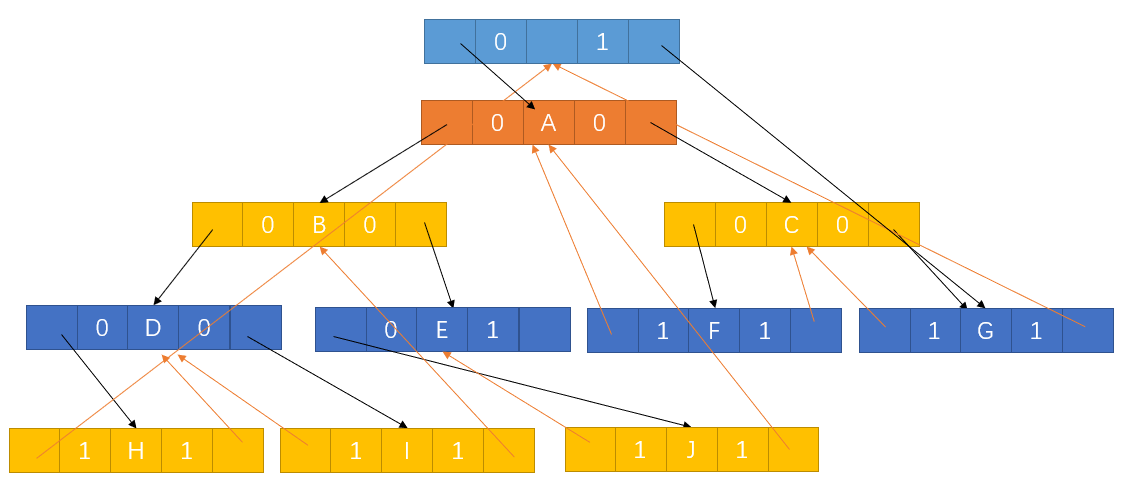
让头结点衔接并中序让节点线索化的程序如下:
/* 中序遍历二叉树T,并将其中序线索化,Thrt指向头结点 */ Status InOrderThreading(BiThrTree *Thrt,BiThrTree T) { *Thrt=(BiThrTree)malloc(sizeof(BiThrNode)); if(!*Thrt) exit(OVERFLOW); (*Thrt)->LTag=Link; /* 建头结点 */ (*Thrt)->RTag=Thread; (*Thrt)->rchild=(*Thrt); /* 右指针回指 */ if(!T) /* 若二叉树空,则左指针回指 */ (*Thrt)->lchild=*Thrt; else { (*Thrt)->lchild=T; pre=(*Thrt); InThreading(T); /* 中序遍历进行中序线索化 */ pre->rchild=*Thrt; pre->RTag=Thread; /* 最后一个结点线索化 */ (*Thrt)->rchild=pre; } return OK; }
因此有了双向链的树之后,我们遍历树的时候就可以不用递归的算法了,此时用中序遍历的非递归算法如下:
/* 中序遍历二叉线索树T(头结点)的非递归算法 */ Status InOrderTraverse_Thr(BiThrTree T) { BiThrTree p; p=T->lchild; /* p指向根结点 */ while(p!=T) { /* 空树或遍历结束时,p==T */ while(p->LTag==Link) p=p->lchild; while(p->RTag==Thread&&p->rchild!=T) { p=p->rchild; visit(p->data); /* 访问后继结点 */ } p=p->rchild; } return OK; }
总结:线索二叉树的使用有:先定义一个线索二叉树的数据类型,先序遍历输入数据,中序遍历线索化,中序遍历连接头指针,中序非递归遍历树。
(2)一般树和森林的存储
一般来说是将树和森林转换为二叉树存储,然后使用先序遍历遍历整个二叉树。转换实例如下:
一般树转换为二叉树:
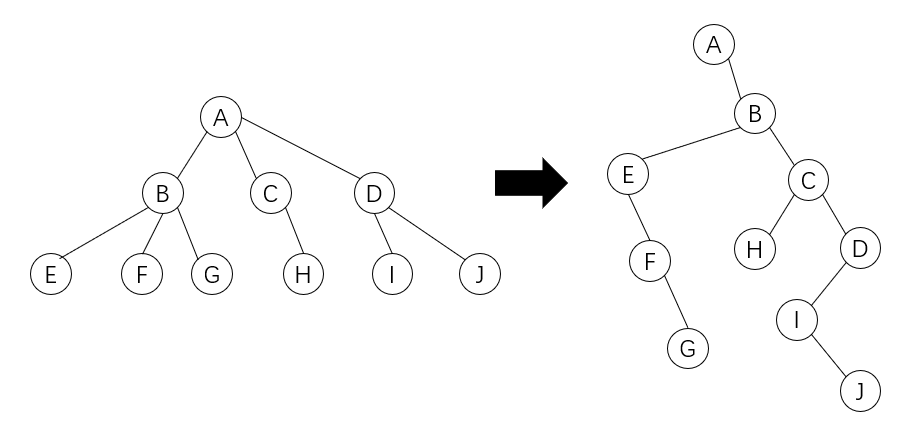
森林转换为二叉树:
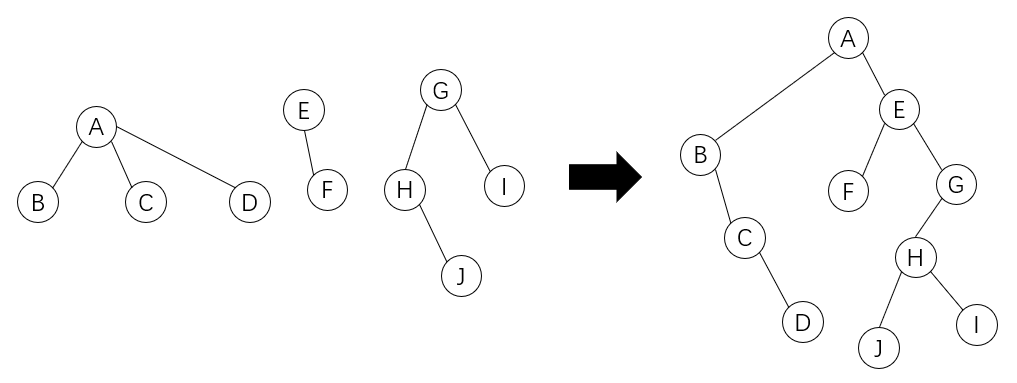
六、特殊的例子----哈夫曼树和哈夫曼编码
从树中一个节点到另一个节点之间的分支构成两个节点之间的路径,路径上的分支数目称为路径长度。树的路径长度就是从树根到每一节点的路径长度之和。
现实中有很多带百分比的情况,比如成绩0-59占5%,60-69占15%,70-79占40%,80-89占30%,90-100占10%。用不同方法写程序,就有不同的二叉树形态。例如对此我们可以得到两种二叉树,如下:
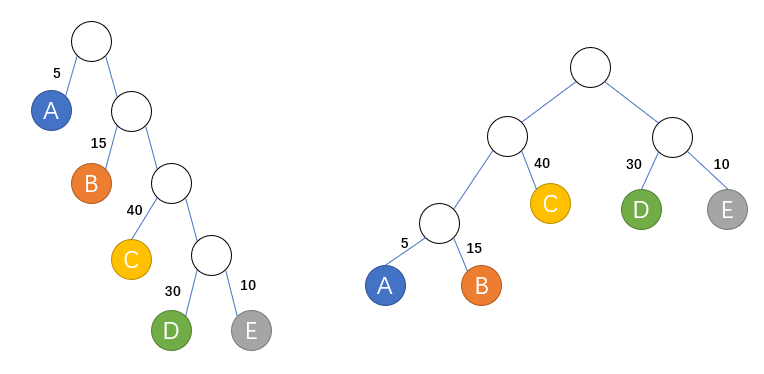
第一种带权路劲长度(WPL):5*1+15*2+40*3+30*4+10*5=315;
第二种带权路径长度(WPL):5*3+15*3+40*2+30*2+10*2=220;
WPL最小的二叉树称做哈夫曼树,哈夫曼树的生成方法:从最小的权值开始往上堆叠。
哈夫曼编码与哈夫曼树有很大的关系,首先统计各个字母所占权重,然后左边换为0,有换为1,如下:
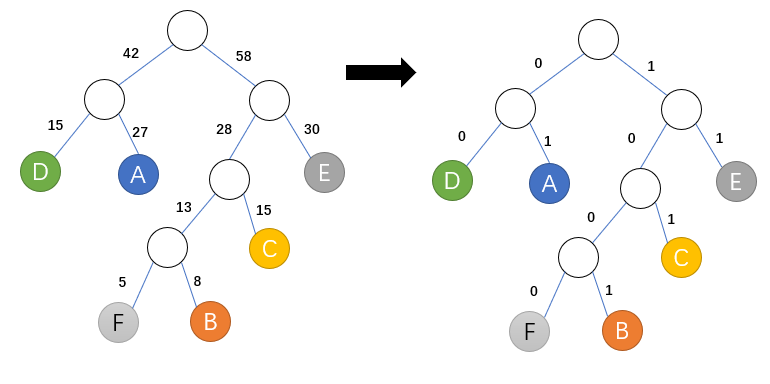
所以A:01 B:1001 C:101 D:00 E:11 F:1000
而且这类编码任意一个编码的前缀都不是其余编码。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号