编程基础1: 用补码去表达整数
在日常生活中,我们常用十进制的数字,在本文主要讨论在程序的世界中如何去存储一个整数(暂不讨论小数)。
一、二进制
现代电子计算机的基本存储和计算单元(如晶体管、逻辑门等)都只有开(1)和关(0)的状态,
开(导通) → 1
关(不导通) → 0
所以在程序的世界都采用二进制来表达数据。
例如 浮栅晶体管(Floating Gate Transistor, FGT)是一种特殊类型的 MOSFET(Metal-Oxide-Semiconductor Field-Effect Transistor, 金属氧化物半导体场效应晶体管),广泛用于闪存(Flash Memory),如 SSD、USB、EEPROM 等存储设备。
浮栅晶体管的核心作用是利用电荷存储数据:
写入(Program):通过高压(隧道效应),将电子注入浮栅,使其带负电。
擦除(Erase):施加反向高压,使电子离开浮栅。
读取(Read):检测浮栅是否带电,决定存储的数据是 0 还是 1。
| 状态 | 表示的二进制数据 |
|---|---|
| 无电荷 | 0 |
| 有电荷 | 1 |
📌 为什么 0 代表带电,1 代表无电?
当浮栅带负电,会阻止电流流动,表示 0。
当浮栅无电荷,电流可以正常流过,表示 1。
设计一个可以表达10种状态的元器件去实现10进制计算机不是完全没可能,只是这样的硬件设计会很复杂,不值得
十进制 → 二进制
示例方法:整数部分采用 “除 2 取余” 法
对于十进制整数,使用不断除以 2,记录余数的方法,直到商为 0,最后倒序排列余数。
示例:将 18₁₀ 转换为二进制
18 ÷ 2 = 9,余 0
9 ÷ 2 = 4,余 1
4 ÷ 2 = 2,余 0
2 ÷ 2 = 1,余 0
1 ÷ 2 = 0,余 1 (商变为 0,停止)
结果:18₁₀ = 10010₂ (倒序排列余数)
二进制 → 十进制
方法:按位展开计算
二进制转换为十进制,使用按位展开,根据 权值 (2ⁿ) 计算。
示例 :将 10010₂ 转换为十进制
按照权重展开:
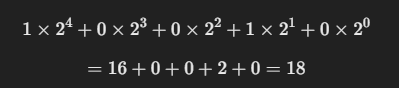
结果:10010₂ = 18₁₀
二、如何表达一个整数
如果不考虑负数的话,好像把十进制转换为二进制,那整数的表达讲完了,但是我们不能忽略负数,并且恰恰是负数给这个事情带来麻烦。
首先我们自然想到设置一个标志位来表示符号。
原码
例如在一个8位的二进制数据种用最高位表示符号,0代表正数,1代表负数。
+5:00000101
-5:10000101
原码缺陷:
- +0(00000000)和 -0(10000000)是两个不同的编码,导致比较和运算时需要额外判断。
- 原码和反码的加减法需要区分符号位,硬件电路复杂:
例如,计算 A - B 时:
先比较 A 和 B 的符号
再决定是做加法还是减法。(例如 -3-5 其实是做加法)
最后调整结果的符号。(例如3-5的结果是负数) - 需要分别设计加法器和减法器电路
反码
现代计算机中已被补码取代:
- 反码的核心作用
-
早期计算机的负数表示
在补码成为标准前,反码是表示有符号整数的常见方式:
规则:负数 = 正数的按位取反(0变1,1变0)。
示例(8位):
+5:00000101
-5:11111010 -
简化减法运算
反码可将减法转换为加法,但需处理循环进位(End-Around Carry):
运算步骤:
将减数取反(转换为负数反码)。
与被减数相加。
若最高位有进位,结果需加1(循环进位)。
示例:7 - 5:
7:00000111
-5(反码):11111010
相加:00000111 + 11111010 = 1 00000001(产生进位)
循环进位:00000001 + 1 = 00000010(结果2,正确)。
- 反码的缺陷
- 零的表示不唯一
+0:00000000
-0:11111111
导致比较和运算时需要额外判断,增加硬件复杂度。 - 运算效率低
循环进位需要额外步骤。
补码
1. 补码的定义
补码是一种用固定位数二进制表示有符号整数的方法。对于 n 位补码:
- 最高位(MSB, Most Significant Bit) 是符号位:
0表示 非负数(正数或零)。1表示 负数。
- 数值范围:
- 最小值:
-2^{n-1}(如 8 位补码的最小值是-128)。 - 最大值:
2^{n-1} - 1(如 8 位补码的最大值是127)。
- 最小值:
2. 补码的计算方法
(1) 正数的补码
正数的补码就是它的原码(直接二进制表示):
- 示例:
+5的 8 位补码:- 原码:
00000101 - 补码:
00000101(与正数原码相同)
- 原码:
(2) 负数的补码
负数的补码计算步骤如下:
- 取绝对值的原码(先当作正数)。
- 按位取反(反码)(
0变1,1变0)。 - 加 1(得到补码)。
示例:求 -5 的 8 位补码:
+5的原码:00000101- 按位取反(反码):
11111010 - 加 1:
11111011(最终补码)
验证:-5 的补码确实是 11111011。
(3) 零的补码
- 零的补码是全 0:
00000000(唯一表示)。 - 补码没有
-0,避免了原码和反码的“零不唯一”问题。
3. 补码的运算规则
补码的核心优势是减法可以转换为加法,无需额外硬件处理符号位。
(1) 加法运算
直接按位相加,丢弃最高位的进位(溢出位)。
- 示例:
7 + (-5)(即7 - 5)7的补码:00000111-5的补码:11111011- 相加:
00000111 + 11111011 --------- 1 00000010 (最高位 1 溢出丢弃) - 结果:
00000010(即2,正确)
(2) 减法运算
A - B 可以转换为 A + (-B),其中 -B 是 B 的补码。
- 示例:
3 - 7(即3 + (-7))3的补码:00000011-7的补码:7的原码:00000111- 反码:
11111000 - 补码:
11111001
- 相加:
00000011 + 11111001 --------- 11111100 - 结果
11111100是负数,转换回十进制:- 补码
11111100→ 反码11111011 - 反码
11111011→ 原码00000100(4) - 所以
11111100=-4(正确)
- 补码
4. 补码的数学本质
补码的本质是模运算(Modular Arithmetic):
- 对于
n位补码,所有运算都在2^n的模数下进行。 - 负数
-x被表示为2^n - x。- 示例(8 位):
-5≡256 - 5 = 251(即11111011)。-128≡256 - 128 = 128(即10000000)。
- 示例(8 位):
这样,A - B 等价于 A + (2^n - B),运算结果自动取模,保证正确性。
补码的魅力值得细细品味,以钟表为例说明:
假设目前的目前时针指向9,忽略分针和秒针。 如果我们要时针指向6,那么有两种办法
- 逆时针转动3格(-3)
- 顺时针转动9格(+9)
同时我们发现3+9=12,这是因为时针有12个刻度(模)。在这种情况下,可以把9看作是-3的补码。
回到一个八位的二进制数,它的模是2^8也就是256.
那么-1 就是256-1 =255( 11111110), -128 就是256-128=128(10000000)
同时神奇地发现,刚好负数的最高位是1,这个最高位可以直接参与加法运算。我认为这是二进制的特性带来的,如果不是二进制,则负数的补码最高位会出现多个可能。
再回到负数的补码计算方式:
- 取绝对值的原码(先当作正数)。
- 按位取反(反码)(
0变1,1变0)。 - 加 1(得到补码)。
为什么负数的补码=反码+1呢?
根据前文已知:负数的补码=模(2^n) -负数的绝对值
根据反码的定义:负数的反码 + 负数绝对值的原码 =2^n-1 (111...111(n个1))
+10 的原码 = 00001010
-10 的反码 = 11110101
相加后 = 11111111
调整一下等式得到:
负数的反码+1 = 2^n(模)-负数绝对值的原码
所以负数的补码=负数的反码+1
5. 补码的优势
| 特性 | 补码(Two's Complement) | 原码(Sign-Magnitude) | 反码(Ones' Complement) |
|---|---|---|---|
| 零的表示 | 唯一(000…00) |
两种(+0 和 -0) |
两种(+0 和 -0) |
| 减法运算 | 直接加法,丢弃溢出位 | 需额外符号判断 | 需循环进位 |
| 硬件实现 | 仅需加法器 | 需加减法两套电路 | 需额外进位处理 |
| 负数范围 | -2^{n-1} 到 2^{n-1}-1 |
-(2^{n-1}-1) 到 2^{n-1}-1 |
-(2^{n-1}-1) 到 2^{n-1}-1 |
| 现代应用 | 所有计算机系统 | 已淘汰 | 仅用于校验和 |
现代计算机普遍采用补码来存储和运算有符号整数
6. 补码(Two's Complement)转换为十进制的方法
补码的最高位(MSB)是符号位:
- 0 表示 正数或零,直接按无符号二进制计算。
- 1 表示 负数,需要先取补码再转换。
1. 正数补码 → 十进制
规则:直接按无符号二进制计算。
示例:
补码 0101 0101(8位):
- 最高位
0→ 正数。 - 计算:
![]()
结果:+85
2. 负数补码 → 十进制
步骤:
- 取反(Invert):所有位取反(
0→1,1→0)。 - 加 1:得到原码的绝对值。
- 加负号:转换为负数。
**示例 **:
补码 1101 1011(8位):
- 最高位
1→ 负数。 - 取反:
1101 1011→0010 0100。 - 加 1:
0010 0100 + 1 = 0010 0101(绝对值37)。 - 加负号:
-37。
结果:-37
7. 常见问题
(1) 为什么补码的最小值是 -128(8 位时)?
- 8 位补码的范围是
-128到127。 10000000被解释为-128(因为-128 = -2^7),没有对应的正数表示。
(2) 如何快速求一个负数的补码?
- 从右向左找到第一个
1,保留这个1及其右侧的所有位。 - 左侧所有位取反。
- 示例:
-5=11111011(第一个1在最右边,左侧全取反)。
- 示例:
(3) 补码的溢出如何处理?
- 如果运算结果超出
n位补码的范围,最高位进位直接丢弃(相当于取模2^n)。 - 示例(8 位):
127 + 1 = 128(超出范围,补码表示为-128,即溢出)。
三、整数的存储方式
- 小端序(Little-Endian):低字节在前(Intel/AMD x86 架构)。
- 大端序(Big-Endian):高字节在前(网络传输、ARM 可选模式)。
示例(32 位整数 0x12345678 的存储):
| 字节地址 | 小端序存储 | 大端序存储 |
|---|---|---|
| 0x0000 | 0x78 |
0x12 |
| 0x0001 | 0x56 |
0x34 |
| 0x0002 | 0x34 |
0x56 |
| 0x0003 | 0x12 |
0x78 |

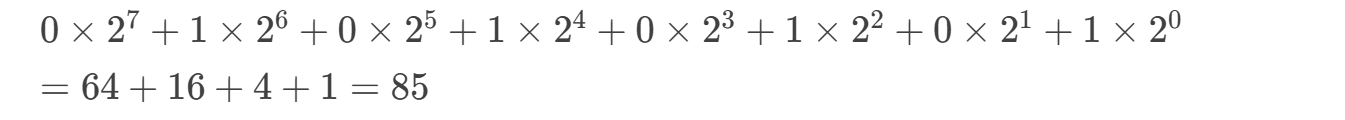

 浙公网安备 33010602011771号
浙公网安备 33010602011771号