斜率优化状态转移——总结

第一部分

简介

为什么称为斜率优化状态转移呢？原因就是为了告诉读者，斜率优化是为了优化状态转移的时间复杂度的，对于转移时间复杂度本来就为 $O(1)$ 的，不能优化。

斜率优化便是通过去除无用的决策点以及研究更优点的性质来优化转移。

基础结构

考虑 $a$ 与 $b$ 单调，且有如下状态转移方程：

$$\begin{align*} \large f_{i}=\min\{f_{j}+a_{i}*b_{j}\} \end{align*}$$

显然，如果暴力转移，时间复杂度是 $O(n)$ 的。

考虑推式子，当下标 $j$ 为下标 $x$ 比选下标 $y$ 更加优。

$$\large \begin{align*} f_{x}+a_{i}\times b_{x} &\ge f_{y}+a_{i}\times b_{y} \\ f_{x}-f_{y} &\ge a_{i}\times b_{y}-a_{i}\times b_{x} \\ f_{x}-f_{y} &\ge a_{i}\times (b_{y}-b_{x})\\ \frac {f_{x}-f_{y}}{b_{y}-b_{x}} &\ge a_{i}\\ \frac {f_{x}-f_{y}}{b_{x}-b_{y}} &\le -a_{i}\\ \end{align*}$$

此时在式中 $\large\frac {f_{x}-f_{y}}{b_{x}-b_{y}}$ 正是斜率的表示形式。

优化过程

考虑将 $b$ 作为横轴，$f$ 作为纵轴。

那么有以下图：

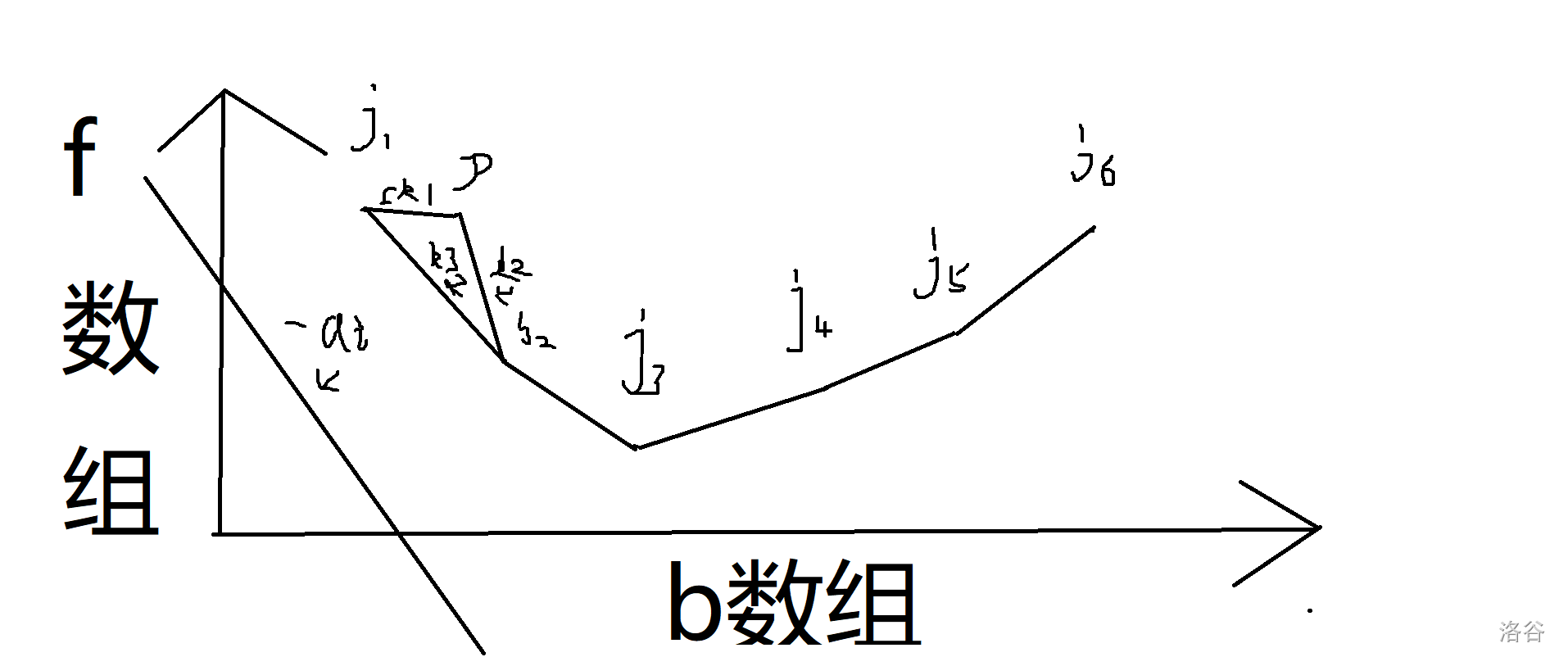
由此图可见，对于决策点 $p$ 来说，无论如何都不可能同时优于 $j1$ 与 $j2$ 两个决策点，所以 $p$ 是一个废点。由此我们还可以知道，对于 $j1-j6$ 中各个点形成的下凸包来说，任意一个点在凸包内部都是废点。

于是考虑维护凸包。

具体是加入新点时，如果发现倒数第二个点连这一个点的斜率小于倒数第二个点连最后一个点的斜率，那么连倒数第二个和这一个点连起来与前面的连线就形成了一个包含最后一个点的凸包。这时候，最后一个点就丸辣。直接将它弹出凸包序列，然后在重复检查弹出的过程，直到倒数第二个点连这一个点的斜率不小于倒数第二个点连最后一个点的斜率。

至于对于不同的 $i$ 从凸包中寻找答案时，查询的方法就很多了，比如当 $-a_{i}$ 不降序时，可以考虑单调队列，具体是凸包序列中的点与后一个点的斜率是单调递增的，如果对于 $-a_{i}$ 都有 $x$ 连 $y$ 的斜率小于等于 $-a_{i}$，那么对于 $-a_{i+1}$ 就还是小于（前面条件，$-a_{i}$ 不降序）。我们有一种通用的方法就是二分，凸包序列本就有单调性，所以二分就是很简单的事情。当然我们还可以用树之类的数据结构来维护（比如本来就支持前驱后继查询的平衡树）。

相信你已经会斜率优化动态规划的转移了，来试试吧！

题目

P3195 [HNOI2008] 玩具装箱

题目描述

P 教授要去看奥运，但是他舍不下他的玩具，于是他决定把所有的玩具运到北京。他使用自己的压缩器进行压缩，其可以将任意物品变成一堆，再放到一种特殊的一维容器中。

P 教授有编号为 $1 \cdots n$ 的 $n$ 件玩具，第 $i$ 件玩具经过压缩后的一维长度为 $C_i$。

为了方便整理，P教授要求：

• 在一个一维容器中的玩具编号是连续的。

• 同时如果一个一维容器中有多个玩具，那么两件玩具之间要加入一个单位长度的填充物。形式地说，如果将第 $i$ 件玩具到第 $j$ 个玩具放到一个容器中，那么容器的长度将为 $x=j-i+\sum\limits_{k=i}^{j}C_k$。

制作容器的费用与容器的长度有关，根据教授研究，如果容器长度为 $x$，其制作费用为 $(x-L)^2$。其中 $L$ 是一个常量。P 教授不关心容器的数目，他可以制作出任意长度的容器，甚至超过 $L$。但他希望所有容器的总费用最小。

输入格式

第一行有两个整数，用一个空格隔开，分别代表 $n$ 和 $L$。

第 $2$ 到 第 $(n + 1)$ 行，每行一个整数，第 $(i + 1)$ 行的整数代表第 $i$ 件玩具的长度 $C_i$。

输出格式

输出一行一个整数，代表所有容器的总费用最小是多少。

数据范围

对于全部的测试点，$1 \leq n \leq 5 \times 10^4$，$1 \leq L \leq 10^7$，$1 \leq C_i \leq 10^7$。

Solution

几乎是板题了，读者只需要把状态转移方程列出来，最后推式子优化就可以了，题目数据非常水。

Code

单调队列：

//单调队列QwQ
#include <bits/stdc++.h>
#define int long long
#define upp(a,x,y) for(int a=x;a<=y;a++)
#define dww(a,x,y) for(int a=y;a>=x;a--)
using namespace std;
const int N = 5e4 + 10;
int n, l, sum[N], dp[N];
int y(int x) {return dp[x] + (sum[x] + l) * (sum[x] + l);}
double kk(int j1, int j2) {return (double)(y(j2) - y(j1)) / (double)(sum[j2] - sum[j1]);}
deque<int> q;//直接上stl，什么叫手写队列？
signed main() {
    cin >> n >> l; l++;
    upp(i, 1, n) cin >> sum[i], sum[i] += sum[i - 1] + 1;
    q.push_front(0);//注意初始化捏
    upp(i, 1, n) {//k 单调递增
        while (q.size()>1 && kk(q.front(), q[1]) <= 2 * sum[i]) q.pop_front();
        int j = q.front();//队头即为答案
        dp[i] = sum[i] * sum[i] - 2 * sum[i] * l + dp[j] + (sum[j] + l) * (sum[j] + l) - 2 * sum[i] * sum[j];
        while (q.size()>1 && kk(q[q.size()-2], i) <= kk(q[q.size() - 2], q.back())) q.pop_back();
        q.push_back(i);
    }
    cout << dp[n];
    return 0;
}

二分：

//二分QwQ
#include <bits/stdc++.h>
#define int long long
#define upp(a,x,y) for(int a=x;a<=y;a++)
#define dww(a,x,y) for(int a=y;a>=x;a--)
using namespace std;
const int N = 5e4 + 10;
int n, l, sum[N], dp[N];
int y(int x) { return dp[x] + (sum[x] + l) * (sum[x] + l); }
double kk(int j1, int j2) { return (double)(y(j2) - y(j1)) / (double)(sum[j2] - sum[j1]); }
deque<int> q;//直接上stl，什么叫手写队列？
signed main() {
    cin >> n >> l; l++;
    upp(i, 1, n) cin >> sum[i], sum[i] += sum[i - 1] + 1;
    q.push_front(0);//注意初始化捏
    upp(i, 1, n) {
        int ll = 0, rr = q.size() - 2;
        while (ll < rr) {
            int mid = ll + rr >> 1;
            if (kk(q[mid], q[mid + 1]) > 2 * sum[i]) rr = mid;
            else ll = mid + 1;
        }
        int j;
        if (q.size() <= 2|| kk(q[rr], q[rr + 1]) <= 2 * sum[i]) j = q.back();
        else j = q[rr];
        dp[i] = sum[i] * sum[i] - 2 * sum[i] * l + dp[j] + (sum[j] + l) * (sum[j] + l) - 2 * sum[i] * sum[j];
        while (q.size() > 1 && kk(q[q.size() - 2], i) <= kk(q[q.size() - 2], q.back())) q.pop_back();
        q.push_back(i);
    }
    cout << dp[n];
    return 0;
}

Let's practice

• 玩具装箱
• 仓库建设
• 特别行动队
• 保护出题人
• 任务安排1
• 任务安排2 (提示：二分)

第二部分

简介

接下来的内容，普及组几乎不可能会涉及，此部分需要读者会线段树，动态开点线段树等数据结构，以及 CDQ 分治。本部分可能较上部分内容来说更难懂一些。但是以后稍加琢磨后就可以较为轻松的对待斜率优化这一难点。（笔者还没有掌握后部分内容 /ll

目录

• 决策的另外一种意义
• 李超线段树（可以直接看动态开店李超线段树）
• 动态开店李超线段树
• CDQ分治
• Let's practice

决策的另外一种意义

考虑上文的转移方程

$$\large \begin{align*} f_{i}&={f_{j}+a_{i}*b_{j}} \end{align*}$$

令

$$\large \begin{align*} y=f_{i}，b=f_{j},k=b_{j},x=a_{i} \end{align*}$$

那么原式变为

$$\large \begin{align*} y=kx+b \end{align*}$$

即为一次函数直线的表达式。

那么每次的新增点其实就是一条直线，因此每次我们决策点其实就是在众多直线中选取 $x=a_{i}$ 时 $y$ 最小的那个直线。

李超线段树

李超线段树便是维护我们上述的直线的，它是一种对于线段树的改版，由学军中学李超提出。

李超线段树实际上并不难，只要读者清楚李超线段树的思想，就很容易学会了。

我们探讨的李超线段树支持以下操作：

• 加入一条直线
• 查询众多直线在 $x=k$ 处 $y$ 的极值（最大/最小）

首先考虑操作 $1$。我们讨论在区间 $[l,r]$ 内的操作。

如果根本没有直线，那么可以直接加入。

如果有直线，那考虑已有直线在 $mid$ 处与新直线的大小关系。

如果新直线在 $mid$ 处取到的值优于旧直线取到的值，就先换直线，然后再在子区间用旧直线更新新直线。

接下来讨论更新左半区间，右半区间，也就是查看两条直线在 $l$ 与 $r$ 处的取值，如果用来更新的那条直线比旧直线在两处的取值要优，那么就递归到相应区间。在 $l=r$ 时，直接讨论大小关系，修改即可。

查询时对于每一个遍历到的区间代表直线，我们都应该更新答案，实际上，每个区间的代表直线都有可能是我们的决策点。

对于更具体的操作可以看代码，以上操作如有不理解也可以看代码。

Code

struct node {
	double k, b;
}line[N];
double calc(int id, int pos) { return line[id].k * bx[pos] + line[id].b; }//bx 为离散化数组，值表示原本位置，下标表示离散化后位置
bool lesd(int x, int y,int pos) {
	return calc(x, pos) < calc(y, pos);
}
struct lctree {
	int a[N * 4];
	void add(int p, int l, int r, int id) {
		if (l == r) {
			if (lesd(id, a[p], l)) a[p] = id;
			return;
		}
		int mid = l + r >> 1;
		if (lesd(id, a[p], mid)) swap(a[p], id);
		if (lesd(id, a[p], l)) add(p * 2, l, mid, id);
		if (lesd(id, a[p], r)) add(p * 2 + 1, mid + 1, r, id);
	}
	double qry(int p, int l, int r, int pos) {
		double res = calc(a[p], pos);
		if (l == r) return res;
		int mid = l + r >> 1;
		if (pos <= mid) res = min(res, qry(p * 2, l, mid, pos));//在左边
		else res = min(res, qry(p * 2 + 1, mid + 1, r, pos));//在右边
		return res;
	}
}tree;

LCtree 真是很简洁呢。