线段树与进阶
目录
- 普通线段树
- 线段树与运用
- 线段树的懒标记
- 线段树进阶
- 动态开点线段树
- 线段树合并与分裂
- 标记永久化线段树
- 可持久化线段树
- zkw 线段树
- *树套树
Part I 普通线段树
主要讲解线段树的常用用法,学会了之后你会发现简单实用,非常牛的一个数据结构。读者在学习的时候可能会有些懵,但只要认真思考,认真学习,就可以学会普通的线段树。
线段树与运用
线段树,顾名思义就是又线段组成的树,现在我们点点讲解线段树。
节点表示
线段树的节点表示 \([l,r]\) 的某种信息,至于信息这个抽象的概念,读者可以理解成区间和,区间最大值,懒标记等题目需要用到的东西。
核心思想
线段树的核心思想是合并二叉树,父节点的信息可以由左右孩子的信息合并而得,举个例子,节点维护区间和信息,父节点表示 \([1,8]\) 区间,左右儿子分别表示 \([1,3],[4,8]\) 区间的和,如果我们知道左右区间的和分别为 \(1,-3\),那么他们的父节点的和就为 \(1+(-3)=-2\)。
线段树一般把左右儿子分为 \([l,\frac{l+r}{2}]\) 与 \([\frac{l+r}{2}+1,r]\) 两个区间,因为这样可以使叶子节点的长度为 \(1\),方便维护,并且可以使平均效率最高,树的深度最低,对于查询,我们最多只会查询 \(\log n\) 的节点数。
合并
写一个将儿子节点信息合并为父节点信息的函数,方便我们使用。
如维护和:
void pu(int x) {sum(x)=sum(ls(x))+sum(rs(x));}
注:\(x\) 表示父节点编号,\(ls(x),rs(x)\) 表示左右节点编号。
建树
建树的目的是为了给每个节点分配意义,也可以设置初始值。
我们采用如果父节点的编号为 \(x\),那么左右儿子的编号分别为 \(2x\) 与 \(2x+1\) 的编号方法,根节点的编号为 \(1\),我们需要建根节点为整个序列区间 \([1,n]\),因为我们都可能用到。根据上面的定义,我们只需要由根节点递归子节点建树即可,把由父节点得来的区间传给儿子。
相当于遍历一遍树节点,有 \(n\log n\) 个,所以时间复杂度为 \(O(n\log n)\)。
Code:
void build(int x,int l,int r) {
l(x)=l,r(x)=r;
if(l==r) return sum(x)=0,void();
int mid=l+r>>1;
build(x*2,l,mid);build(x*2+1,mid+1,r);
pu(x);
}
修改
由于是修改一个节点,直接向下递归修改叶子节点然后向上递归合并信息即可,以下以维护和为例子。由于树的深度为 \(\log n\),所以时间复杂度为 \(O(\log n)\)。
Code:
void change(int x,int pl,int k) {
int l=l(x),r=r(x);
if(l==r&&l==pl) {
sum(x)=k;
return;
}
int mid=l+r>>1;
if(k<=mid) change(x*2,pl,k);//在左儿子这里
else change(x*2+1,pl,k);//在右儿子这里
pu(x);//儿子修改完成,合并儿子的信息
}
查询
直接找到查询区间的几个在线段树上的最大可组合区间。如原来的区间是 \([1,8]\),查询区间为 \([1,3]\)。分成 \([1,2]\) 和 \([3,3]\),而不是 \([1,1],[2,2],[3,3]\),这样是多此一举的,会极大的提高我们的时间复杂度,也就是我们只要发现目前的节点区间完全被包含就不往下递归,对于不完全覆盖的节点,合并子节点对于此区间的特殊信息即可。
时间复杂度是 \(O(n\log n)\),可以发现每层最多四个节点被遍历到:
考虑不完全包含的区间,每层最多有两个,如果有三个及以上,就表明必然不能组成一个连续的区间,比如 \([1,4],[5,8]\) 不完全包含且连续,那么对于 \([1,4]\) 来说,必然是有 \([x,4](x\ne 1)\) 包含在查询区间内,对于 \([5,8]\) 来说,必然有 \([5,y](y\ne 8)\) 包含在查询区间内,然后如果他们两边还有一个,查询的区间就必须接上 \(x,y\),但这是不可能的,因为 \((x\ne 1)(y\ne 8)\)(这个条件如果不达成就是完全包含区间)
考虑完全包含的区间,每层最多有两个,因为如果由三个及以上就必然可以和为上一层的完全包含或者查询区间不连续。
以下是查询区间和的代码。
Code:
int qry(int x,int ll,int rr) {
int l=l(x),r=(x);
if(l>=ll&&r<=rr) return sum(x);
int mid=l+r>>1,sum=0;
if(mid>=ll) sum+=qry(x*2,ll,rr);//左边有在询问区间内的
if(mid<rr) sum+=qry(x*2+1,ll,rr);//右边有在询问区间内的
return sum;
}
线段树
目前为止,我们已经实现了一个支持 \(O(n\log m)\) 的单点修改,区间查询的线段树了。
以下是演示维护区间和的代码。
线段树应该开四倍空间,原因略。
Code:
struct node {
int l,r,sum;
#define l(x) tr[x].l
#define r(x) tr[x].r
#define sum(x) tr[x].sum
}
struct segment_tree {
node tr[N*4];//四倍空间
void pu(int x) {sum(x)=sum(x*2)+sum(x*2+1);}
void build(int x,int l,int r) {
l(x)=l,r(x)=r;
if(l==r) sum(x)=0,void();
int mid=l+r>>1;
build(x*2,l,mid);build(x*2+1,mid+1,r);
pu(x);
}
void change(int x,int pl,int k) {
int l=l(x),r=r(x);
if(l==r) {
sum(x)+=k;
return;
}
int mid=l+r>>1;
if(pl<=mid) change(x*2,pl,k);
else change(x*2+1,pl,k);
pu(x);
}
int qry(int x,int ll,int rr) {
int l=l(x),r=r(x);
if(l>=ll&&r<=rr) return sum(x);
int mid=l+r>>1,sum=0;
if(mid>=ll) sum+=qry(x*2,ll,rr);
else sum+=qry(x*2+1,ll,rr);
return sum;
}
}tree;
另外,希望读者对线段树的代码尽可能的熟悉,也可以自己研究自己的写法(别写炸)。因为如果不熟悉线段树代码,在场上很难写出正确的线段树(或者花费大量时间)。
例题
例题一
P10463 Interval GCD
发现 \(\gcd(x,y)=\gcd(x,y-x)\),由此思考,发现 \(\gcd(x,y,z)=\gcd(x,y-x,z-y)\),对于任意个数都有如上,证明易证。于是我们用线段树维护差分数组,\(\gcd(a_{l\dots r})=\gcd(a_{l},\gcd(b_{l+1\dots r}))\)。因为 \(a_{l}=\sum_{i=1}^{l} b_{i}\),对差分数组 \(b\) 维护区间最大公约数以及区间和即可。
这里我懒得用两颗线段树了,用了一颗树状数组。
Code:
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=5e5+10;
int a[N],b[N],n,m;
struct BIT_TREE {
int t[N];
int lowbit(int x) {
return x&-x;
}
void add(int x,int k) {
for(int i=x;i<=n+1;i+=lowbit(i)) t[i]+=k;
}
void change(int l,int r,int k) {
add(l,k);add(r+1,-k);
}
int qry(int x) {
int sum=0;
for(int i=x;i;i-=lowbit(i)) sum+=t[i];
return sum;
}
}tree1;
struct node {
int l,r,gcd;
#define l(x) tr[x].l
#define r(x) tr[x].r
#define gcd(x) tr[x].gcd
};
struct segment_tree {
node tr[N*4];
void pu(int x) {
gcd(x)=__gcd(abs(gcd(x*2)),abs(gcd(x*2+1)));
}
void build(int x,int l,int r) {
l(x)=l,r(x)=r;
if(l==r) {
gcd(x)=b[l];
return;
}
int mid=l+r>>1;build(x*2,l,mid);build(x*2+1,mid+1,r);
pu(x);
}
void change(int x,int p,int k) {
int l=l(x),r=r(x);
if(l==r&&l==p) {
gcd(x)+=k;
return;
}
int mid=l+r>>1;
if(p<=mid) change(x*2,p,k);
else change(x*2+1,p,k);
pu(x);
}
int qry(int x,int ll,int rr) {
int l=l(x),r=r(x);
if(l>=ll&&r<=rr) return gcd(x);
int mid=l+r>>1,gcd=-1;
if(ll<=mid) {
if(gcd==-1) gcd=abs(qry(x*2,ll,rr));
else gcd=__gcd(gcd,abs(qry(x*2,ll,rr)));
}
if(rr>mid) {
if(gcd==-1) gcd=abs(qry(x*2+1,ll,rr));
else gcd=__gcd(gcd,abs(qry(x*2+1,ll,rr)));
}
return gcd;
}
}tree;
signed main() {
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i],b[i]=a[i]-a[i-1],tree1.add(i,b[i]);
tree.build(1,1,n+1);
while(m--) {
char op;int l,r,d;
cin>>op;
if(op=='C') {
cin>>l>>r>>d;
tree.change(1,l,d);
tree.change(1,r+1,-d);
tree1.change(l,r,d);
}
else {
cin>>l>>r;
if(l==r) {
cout<<abs(tree1.qry(l))<<endl;
continue;
}
cout<<__gcd(abs(tree1.qry(l)),tree.qry(1,l+1,r))<<endl;
}
}
return 0;
}
例题二
P4145 上帝造题的七分钟 2 / 花神游历各国
有区间修改怎么办呢?注意到每个数被开方后大于 \(1\) 的次数不会超过 \(\log \log 10^{12}+1\)。
对于修改操作,设势能为不是 \(1\) 的数的个数,对于一个区间,如果所有数都是 \(1\) 就不遍历,那么将势能减一的最大代价就是 \(O(\log \log V \log n)\)。
当势能为 \(0\) 时,所有修改操作的时间复杂度为 \(O(1)\)。查询一直是 \(O(\log n)\)。
所以总时间复杂度不会超过 \(O(n \log \log V \log n+m \log n)\)。
懒标记
这里不介绍扫描线,请读者自己学习。
如果我们想要区间修改,怎么办呢?一个令人开心的回答是,我们可以用懒标记轻易实现总时间复杂度不变的区间修改。
懒标记就是字面意思,就是我们懒得子区间的修改,只有到迫不得已,下传会影响答案时再下传。由上面的推论,我们每次查询最多经过 \(\log\) 的个节点。于是我们把修改像区间查询分成 \(\log\) 的个全部包括的大区间,初步标记懒标记,就不用管了。然后等待下次用到时再下传即可。这样进行一次初步标记的时间复杂度与区间查询一样 \(O(\log n)\)。
要注意的,在初步标记时也需之前下传标记,因为父节点等于子节点的和,如果不下传,就会被没被父节点的修改影响的子节点更新,如果下次询问区间直接是父节点的区间,就会直接返回父节点的值,然而是错的。
Code:
void pd(int x) {
if(lz(x)) {
lz(x*2)+=lz(x);lz(x*2+1)+=lz(x);
sum(x*2)+=(r(x*2)-l(x*2)+1)*lz(x);
sum(x*2+1)+=(r(x*2+1)-l(x*2+1)+1)*lz(x);
lz(x)=0;
}
}
void change(int x,int ll,int rr,int k) {
int l=l(x),r=r(x);
if(l>=ll&&r<=rr) {
sum(x)+=k;
return;
}
pd(x);
int mid=l+r>>1;
if(ll<=mid) change(x*2,ll,rr,k);
if(mid<rr) change(x*2+1,ll,rr,k);
pu(x);
}
int qry(int x,int ll,int rr) {
int l=l(x),r=r(x);
if(l>=ll&&r<=rr) return sum(x);
int mid=l+r>>1,sum=0;
pd(x);
if(mid>=ll) sum+=qry(x*2,ll,rr);
else sum+=qry(x*2+1,ll,rr);
pu(x);
return sum;
}
例题一
洛谷 P1558 色板游戏
现在有一个长为 \(n\) 的序列 \(a\),有 \(q\) 次询问,每次询问修改 \([l,r]\) 的数为 \(c\),或者查询 \([l,r]\) 里有多少个不同的数。\(c,a_{i} \le m,m\le 30\)。
考虑区间信息加,我们需要知道 \([l,r]\) 有多少个不同的数,光是这个信息不可以加。但是我们转化成求 \(k\) 的
个数,\(k\) 满足条件 \(\exists i \in [l,r],a_{i}=k\)。对于单个 \(k\) 的满足性,满足可加性。于是套板子然后查询时枚举 \(k\) 是否满足累加即可,时间复杂度 \(O(mn \log n)\)。
代码:
// Problem: P1558 色板游戏
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P1558
// Memory Limit: 128 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
#define int long long
#define upp(a, x, y) for (int a = x; a <= y; a++)
#define dww(a, x, y) for (int a = x; a >= y; a--)
#define pb(x) push_back(x)
#define endl '\n'
#define x first
#define y second
#define PII pair<int, int>
using namespace std;
const int N = 1e5 + 10;
int a[N];
struct node {
int l, r, lz;
bool sum[31];
#define l(x) tr[x].l
#define r(x) tr[x].r
#define lz(x) tr[x].lz
#define sum(x, y) tr[x].sum[y]
};
struct segtree {
node tr[N * 8];
auto merge(node l, node r) {
l.r = r.r;
upp(i, 1, 30) l.sum[i] |= r.sum[i];
return l;
}
void pu(int x) {
upp(i, 1, 30) { sum(x, i) = sum(x * 2, i) | sum(x * 2 + 1, i); }
}
void pd(int x) {
if (lz(x)) {
lz(x * 2) = lz(x * 2 + 1) = lz(x);
upp(i, 1, 30) sum(x * 2, i) = sum(x * 2 + 1, i) = 0;
sum(x * 2, lz(x)) = sum(x * 2 + 1, lz(x)) = 1;
lz(x) = 0;
}
}
void build(int x, int l, int r) {
l(x) = l, r(x) = r, lz(x) = 0;
if (l == r) {
upp(i, 2, 30) sum(x, i) = 0;
sum(x, 1) = 1;
return;
}
int mid = l + r >> 1;
build(x * 2, l, mid), build(x * 2 + 1, mid + 1, r);
pu(x);
}
void change(int x, int ll, int rr, int k) {
int l = l(x), r = r(x);
if (l >= ll && r <= rr) {
lz(x) = k;
upp(i, 1, 30) sum(x, i) = 0;
sum(x, k) = 1;
return;
}
pd(x);
int mid = l + r >> 1;
if (ll <= mid) change(x * 2, ll, rr, k);
if (mid < rr) change(x * 2 + 1, ll, rr, k);
pu(x);
}
auto qry(int x, int ll, int rr) {
int l = l(x), r = r(x);
if (l >= ll && r <= rr) return tr[x];
int mid = l + r >> 1;
pd(x);
node now;
if (ll <= mid) {
if (mid < rr)
now = merge(qry(x * 2, ll, rr), qry(x * 2 + 1, ll, rr));
else
now = qry(x * 2, ll, rr);
} else
now = qry(x * 2 + 1, ll, rr);
pu(x);
return now;
}
} t1;
signed main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
int n, m, q;
cin >> n >> m >> q;
t1.build(1, 1, n);
while (q--) {
char op;
cin >> op;
if (op == 'C') {
int l, r, x;
cin >> l >> r >> x;
if(l>r) swap(l,r);
t1.change(1, l, r, x);
} else {
int l, r;
cin >> l >> r;
if(l>r) swap(l,r);
auto tmp = t1.qry(1, l, r);
int sum = 0;
upp(i, 1, 30) if (tmp.sum[i]) sum++;
cout << sum << endl;
}
}
return 0;
}
例题二
P3373 【模板】线段树 2
这题主要在于如何处理两个修改。
对于 pushdown() 来说,所有懒标记必须按照一定的顺序执行。如果我们先加再乘,那么我们无法处理不受乘法影响的加法(可以离线处理)。如果我们先乘再加,那么我们再修改乘的懒标记的时候,运用乘法结合律,就可以对于加的懒标记乘,最后先乘再加即可。
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+10;
struct node {
int l,r,sum,tgp,tgm;
#define l(x) tr[x].l
#define r(x) tr[x].r
#define sum(x) tr[x].sum
#define tgp(x) tr[x].tgp
#define tgm(x) tr[x].tgm
}tr[N*4];
int a[N];
int n,q,m;
void build(int x,int l,int r) {
l(x)=l,r(x)=r;
tgm(x)=1;
if(l==r) {
sum(x)=a[l]%m;
return;
}
int mid=l+r>>1;
build(x*2,l,mid);build(x*2+1,mid+1,r);
sum(x)=(sum(x*2)+sum(x*2+1))%m;
}
void pushdown(int x) {
sum(x*2)=(sum(x*2)*tgm(x))%m;
sum(x*2)=(sum(x*2)+(r(x*2)-l(x*2)+1)%m*tgp(x))%m;
sum(x*2+1)=(sum(x*2+1)*tgm(x))%m;
sum(x*2+1)=(sum(x*2+1)+(r(x*2+1)-l(x*2+1)+1)%m*tgp(x))%m;
tgm(x*2)=(tgm(x*2)*tgm(x))%m;tgm(x*2+1)=(tgm(x*2+1)*tgm(x))%m;
tgp(x*2)=(tgp(x*2)*tgm(x))%m;tgp(x*2+1)=(tgp(x*2+1)*tgm(x))%m;
tgp(x*2)=(tgp(x*2)+tgp(x))%m;tgp(x*2+1)=(tgp(x*2+1)+tgp(x))%m;
tgp(x)=0,tgm(x)=1;
}
void change_plus(int x,int ll,int rr,int k) {
int l=l(x),r=r(x);
if(l>=ll&&r<=rr) {
tgp(x)=(tgp(x)+k)%m;
sum(x)=(sum(x)+(k*((r-l+1)%m)%m)%m)%m;
return;
}
pushdown(x);
int mid=l+r>>1;
if(ll<=mid) change_plus(x*2,ll,rr,k);
if(rr>mid) change_plus(x*2+1,ll,rr,k);
sum(x)=sum(x*2)+sum(x*2+1);
}
void change_mul(int x,int ll,int rr,int k) {
int l=l(x),r=r(x);
if(l>=ll&&r<=rr) {
tgm(x)=tgm(x)*k%m;
tgp(x)=tgp(x)*k%m;
sum(x)=sum(x)*k%m;
return;
}
pushdown(x);
int mid=l+r>>1;
if(ll<=mid) change_mul(x*2,ll,rr,k);
if(rr>mid) change_mul(x*2+1,ll,rr,k);
sum(x)=sum(x*2)+sum(x*2+1);
}
int qry(int x,int ll,int rr) {
int l=l(x),r=r(x);
if(l>=ll&&r<=rr) {
return sum(x);
}
pushdown(x);
int mid=l+r>>1,sum=0;
if(ll<=mid) sum=(sum+qry(x*2,ll,rr))%m;
if(rr>mid) sum=(sum+qry(x*2+1,ll,rr))%m;
return sum;
}
signed main() {
cin>>n>>q>>m;
for(int i=1;i<=n;i++) cin>>a[i];
build(1,1,n);
while(q--) {
int x;
cin>>x;
if(x==1) {
int a,b,k;
cin>>a>>b>>k;
change_mul(1,a,b,k);
}
else if(x==2) {
int a,b,k;
cin>>a>>b>>k;
change_plus(1,a,b,k);
}
else {
int a,b;
cin>>a>>b;
cout<<qry(1,a,b)<<endl;
}
}
return 0;
}
例题三
P2572 [SCOI2010] 序列操作
对于查询有多少个一是简单的,所以我们具体讨论如何维护连续。修改懒标记,具体维护下面讨论。
抛开取反操作,我们为了合并信息,再维护当前段的左起/右起连续的数量即可,合并时候单个信息各个合并,对于询问的答案(最大连续 \(1\) 的数量)分讨取最大值。
有了区间取反操作,所有的 \(1\) 会变成 \(0\),所有的 \(0\) 会变成 \(1\)。因此,我们维护同样之前的信息,但是对象变为 \(0\),如果遇到取反操作,直接将区间中 \(0\) 和 \(1\) 的答案交换即可。
两个操作如何结合请读者自己思考。
这里放上代码(之前写的,码风不太好)。
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+10;
struct node {
int l,r;
int sum1,suml1,sumr1,sumk1;
int sum0,suml0,sumr0,sumk0;
int tg1,tg2;
#define l(x) tr[x].l
#define r(x) tr[x].r
#define sum1(x) tr[x].sum1
#define suml1(x) tr[x].suml1
#define sumr1(x) tr[x].sumr1
#define sumk1(x) tr[x].sumk1
#define sum0(x) tr[x].sum0
#define suml0(x) tr[x].suml0
#define sumr0(x) tr[x].sumr0
#define sumk0(x) tr[x].sumk0
#define tg1(x) tr[x].tg1
#define tg2(x) tr[x].tg2
}tr[N*4];
int n,m;
int w[N];
node merge(node ls,node rs,int l,int r,int tg1,int tg2) {
return (node){l,r,ls.sum1+rs.sum1,
(ls.sum0?ls.suml1:ls.sum1+rs.suml1),(rs.sum0?rs.sumr1:rs.sum1+ls.sumr1),
max(max(ls.sumk1,rs.sumk1),ls.sumr1+rs.suml1),ls.sum0+rs.sum0,
(ls.sum1?ls.suml0:ls.sum0+rs.suml0),(rs.sum1?rs.sumr0:rs.sum0+ls.sumr0),
max(max(ls.sumk0,rs.sumk0),ls.sumr0+rs.suml0),tg1,tg2};
}
void build(int x,int l,int r) {
l(x)=l,r(x)=r;
if(l==r) {
sum1(x)=suml1(x)=sumr1(x)=sumk1(x)=w[l];
sum0(x)=suml0(x)=sumr0(x)=sumk0(x)=!w[l];
tg1(x)=-1,tg2(x)=0;
return;
}
int mid=l+r>>1;
build(x*2,l,mid),build(x*2+1,mid+1,r);
tr[x]=(node)merge(tr[x*2],tr[x*2+1],l,r,(int)-1,(int)0);
}
void mktg(int x,int tp) {
int len=r(x)-l(x)+1;
if(tp==0) tr[x]={l(x),r(x),0,0,0,0,len,len,len,len,0,0};
if(tp==1) tr[x]={l(x),r(x),len,len,len,len,0,0,0,0,1,0};
if(tp==2) tg2(x)^=1,swap(suml0(x),suml1(x)),swap(sumr0(x),sumr1(x)),swap(sumk0(x),sumk1(x)),swap(sum0(x),sum1(x));
}
void pushdown(int x) {
if(~tg1(x)) mktg(x*2,tg1(x)),mktg(x*2+1,tg1(x));
if(tg2(x)) mktg(x*2,2),mktg(x*2+1,2);
tg1(x)=-1,tg2(x)=0;
}
void change(int x,int ll,int rr,int tp) {
int l=l(x),r=r(x);
if(l>=ll&&r<=rr) {
mktg(x,tp);
return;
}
pushdown(x);
int mid=l+r>>1;
if(mid>=ll) change(x*2,ll,rr,tp);
if(mid<rr) change(x*2+1,ll,rr,tp);
tr[x]=merge(tr[x*2],tr[x*2+1],l,r,tg1(x),tg2(x));
}
node qry(int x,int ll,int rr) {
int l=l(x),r=r(x);
if(l>=ll&&r<=rr) {
return tr[x];
}
pushdown(x);
int mid=l+r>>1;
if(mid>=rr) return qry(x*2,ll,rr);
if(mid<ll) return qry(x*2+1,ll,rr);
node a=qry(x*2,ll,rr),b=qry(x*2+1,ll,rr),c;
c=merge(a,b,(int)0,(int)0,(int)0,(int)0) ;
return c;
}
signed main() {
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>w[i];
build(1,1,n);
while(m--) {
int c,x,y;
cin>>c>>x>>y;x++,y++;
if(c==0) change(1,x,y,0);
else if(c==1) change(1,x,y,1);
else if(c==2) change(1,x,y,2);
else if(c==3) cout<<qry(1,x,y).sum1<<endl;
else cout<<qry(1,x,y).sumk1<<endl;
}
return 0;
}
例题四
P4644 [USACO05DEC] Cleaning Shifts S
以 \(f_{i}\) 为 \(1 \dots i\) 时间段全部值班的最小代价。
如果有三元组 \((x,y,z)\),有以下状态转移方程:
为了转移的顺序性,考虑把每个元组按前二元排序,再按从前到后的顺序转移。
时间复杂度 \(O(m^2)\),为了快速转移,我们用线段树维护 \(f_{i}\),这样就可以用 \(O(\log m)\) 的时间复杂度查询 \(1\) 到 \(y-1\) 的 \(f_{i}\) 最值,于是我们实现了 \(O(\log m)\) 的转移。
总时间复杂度:\(O(m \log m)\)。
注意初始化负无穷。
例题五
P8969 幻梦 | Dream with Dynamic
最终 BOSS 来了。
这题的难点就在于如何处理 P 操作,我们完全无法合并两个 P 操作或者合并两个 AP/PA 操作!这导致我们无法以正确的时间复杂度获取答案,比如说对于 \(4\) 这个点我们要做 P 操作,只能一个一个的做,但是由于 P 是区间操作,我们最多会有 \(3\times 10^{11}\) 个 P 操作等待处理。
但是,你有没有注意到一点?参考花神游历各国,我们只需要进行不多的 P 操作,最后那个数就会变成 \(0\),但是这意味着我们就可以暴力了吗?因为还有 A 可以将势能一次性增加 \(n\)(设势能为不为 \(0\) 的数的个数)。难道这个观察就没用了吗?它至少可以告诉我们 P 操作会把原值减很多很多,那至于会减多少呢?一个数 \(x\) 经过 P 操作过后,其值不超过 \(\log x+1\)。
也就是说,设 \(x\) 经过 P 操作后的值为 \(P(x)\),\(P(x)\) 的值域为 \([0,\log x+1]\)。
既然我们无法找到一个可以 \(O(1)\) 计算多个 \(P\) 和 \(A\) 复合的函数,我们就自己拟定函数 \(F(x,list)\) 表示 \(x\) 经过所有 \(list\) 操作的值,这个函数实际上一个表,支持 \(O(1)\) 询问(即提前处理好),请注意这或许可以作为一个套路出现。对于这个函数,设定义域为 \(T\),我们即可 \(O(T)\) 复合两个函数 \(F(x,\{P,A\})=F(F(x,\{P\}),\{A\})\),我们需要让定义域尽可能小,因为操作传递的时候,对于每个节点都有一个独特的 \(list\)。
上文我们知道了 \(P(x)\) 的值域很小,而复合函数最后内层函数的值域会变成外层函数的定义域(这里定义域指的是我们有可能查询到的 \(x\) 的集合),所以这里我们要避免将 A 作为 \(list\) 的最后一个值。而对于两个 A 操作,本来我们就可以合并(基础加函数),\(A(x)+A(y)=A(x+y)\)。对于连续的两个 P,我们可以看作中间有一个加 \(0\) 操作。
A 可以对于单独的 P 操作进行 \(O(1)\) 合并。
为了处理结尾是 A 的,我们对于所有 P 的初标记,都对于其所有最大区间儿子(满足映射函数一致)做合并 AP。这保证任何从上传递至少含一个 P 的时候,被更新的序列都是由 P 结尾。
如果目前标记全不是 P,则 A 作为标记,直接对于答案加上就行了。并且当且仅当是最后一个的时候才有可能是 A。
对于 P 的初标记传递,考虑势能分析。设势能为 P 标记的数量。我们花费 \(O(\log V)\) 的代价让势能减一。每次 pushdown 会使势能增加一,总共有 \(O(q \log n)\) 的次数 pushdown,所以均摊复杂度为 \(O(\log n\log V)\)。
详细讲解一下 pushdown,我们优先复合两个函数,然后如果有 A 操作在尾部,就下传。
至此,我们解决了这个问题。
// Problem: P8969 幻梦 | Dream with Dynamic
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P8969
// Memory Limit: 1 MB
// Time Limit: 10000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
#define int long long
#define upp(a, x, y) for (int a = x; a <= y; a++)
#define dww(a, x, y) for (int a = x; a >= y; a--)
#define pb(x) push_back(x)
#define endl '\n'
#define x first
#define y second
#define PII pair<int, int>
using namespace std;
const int N = 3e5 + 10, M = 55;
int a[N], n, m;
struct node {
int l, r, lz1, lz2; // lz1 add,lz2 popc
int pre[M];
#define l(x) tr[x].l
#define r(x) tr[x].r
#define lz1(x) tr[x].lz1
#define lz2(x) tr[x].lz2
#define pre(x, y) tr[x].pre[y]
};
int popc(int x) {
bitset<100> S(x);
return S.count();
}
struct segtree {
node tr[N * 4];
void build(int x = 1, int l = 1, int r = n) {
l(x) = l, r(x) = r;
upp(i, 0, 50) pre(x, i) = i;
if (l == r) {
lz1(x) = a[l];
lz2(x) = 1;
return;
}
int mid = l + r >> 1;
build(x * 2, l, mid);
build(x * 2 + 1, mid + 1, r);
}
void mkad(int x) { // add 在 popc 前,合并处理两个操作 (ap)
upp(i, 0, 50) pre(x, i) = popc(pre(x, i) + lz1(x));
lz1(x) = 0;
}
void pd(int x) {
if (lz2(x)) {
upp(i, 0, 50) {
pre(x * 2, i) = pre(x, pre(x * 2, i));
pre(x * 2 + 1, i) = pre(x, pre(x * 2 + 1, i));
}
upp(i, 0, 50) pre(x, i) = i;
lz2(x * 2) = lz2(x * 2 + 1) = 1, lz2(x) = 0;
}
if (lz1(x)) lz1(x * 2) += lz1(x), lz1(x * 2 + 1) += lz1(x), lz1(x) = 0;
}
void upd(int x, int l, int r) {
if (lz2(x)) {
cout << "**" << l << ' ' << r << endl;
return mkad(x);
}
pd(x);
int mid = l + r >> 1;
upd(x * 2, l, mid);
upd(x * 2 + 1, mid + 1, r);
}
void add(int ll, int rr, int k, int x = 1, int l = 1, int r = n) {
if (l >= ll && r <= rr) {
lz1(x) += k;
return;
}
pd(x);
int mid = l + r >> 1;
if (ll <= mid) add(ll, rr, k, x * 2, l, mid);
if (rr > mid) add(ll, rr, k, x * 2 + 1, mid + 1, r);
}
void pc(int ll, int rr, int x = 1, int l = 1, int r = n) {
if (l >= ll && r <= rr) {
upd(x, l, r);
lz2(x) = 1;
return;
}
pd(x);
int mid = l + r >> 1;
if (ll <= mid) pc(ll, rr, x * 2, l, mid);
if (rr > mid) pc(ll, rr, x * 2 + 1, mid + 1, r);
}
int qry(int p, int x = 1, int l = 1, int r = n) {
if (l == r) return pre(x, 0) + lz1(x);
int mid = l + r >> 1;
if (lz2(x)) {
if (p <= mid)
return pre(x, qry(p, x * 2, l, mid)) + lz1(x);
else
return pre(x, qry(p, x * 2 + 1, mid + 1, r)) + lz1(x);
} else {
if (p <= mid)
return qry(p, x * 2, l, mid) + lz1(x);
else
return qry(p, x * 2 + 1, mid + 1, r) + lz1(x);
}
}
} t1;
signed main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
upp(i, 1, n) cin >> a[i];
t1.build();
upp(i, 1, m) {
char op;
int x, y, z;
cin >> op;
if (op == 'J') {
cin >> x;
assert(t1.qry(x) <= 50);
cout << t1.qry(x) << endl;
} else if (op == 'A') {
cin >> x >> y >> z;
t1.add(x, y, z);
} else {
cin >> x >> y;
t1.pc(x, y);
}
}
return 0;
}
Part II 线段树进阶
很有用。
动态开点线段树
本质上,就是我们不会用到所有区间,所以我们仅当用到该区间的时候(即对该区间有任何修改)再创建这个节点。
比如,我们有 \([1,8]\) 这一段,修改 \([1,1]\) 这一段。
首先到 \([1,8]\) 发现未创建,创建。
到 \([1,4]\) 发现未创建,创建。
到 \([1,2]\) 发现未创建,创建。
到 \([1,1]\) 发现未创建,创建并修改。
然后向上合并信息。
如何接下来修改 \([2.2]\) 这一段,那么前面创建过的就不用创建了,我们只需要创建 \([2,2]\) 这个就行了。
依照前面的证明,我们有每次修改最多创建 \(O(\log(n))\) 的节点数。如果值域很大,就可以省掉很多空间。
此时子节点不再是 \(2x\) 和 \(2x + 1\),而是父节点记住子节点的索引,以此访问。
时间复杂度没有变化,但是我们省了很多空间。如果用结构体来写,也很好写。
模板:线段树 1。
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+10;
struct node {
int l,r,sum,lz;
#define l(x) tr[x].l
#define r(x) tr[x].r
#define sum(x) tr[x].sum
#define lz(x) tr[x].lz
};
struct segment_tree {
node tr[4*N];
int cnt,root;
int build() {
++cnt;l(cnt)=r(cnt)=-1;sum(cnt)=lz(cnt)=0;
return cnt;
}
void pu(int x) {
int sum=0;
if(l(x)!=-1) sum+=sum(l(x));
if(r(x)!=-1) sum+=sum(r(x));
sum(x)=sum;
}
void pd(int x,int l,int r) {
int mid=l+r>>1;
if(lz(x)) {
if(l(x)==-1) l(x)=build();
if(r(x)==-1) r(x)=build();
lz(l(x))+=lz(x),lz(r(x))+=lz(x);
sum(l(x))+=(mid-l+1)*lz(x),sum(r(x))+=(r-mid)*lz(x);
lz(x)=0;
}
}
void change(int x,int ll,int rr,int l,int r,int k) {
if(l>=ll&&r<=rr) {
sum(x)=sum(x)+k*(r-l+1);
lz(x)+=k;
return;
}
int mid=l+r>>1;
pd(x,l,r);
if(mid>=ll) {
if(l(x)==-1) l(x)=build();
change(l(x),ll,rr,l,mid,k);
}
if(mid<rr){
if(r(x)==-1) r(x)=build();
change(r(x),ll,rr,mid+1,r,k);
}
pu(x);
}
int qry(int x,int ll,int rr,int l,int r) {
if(l>=ll&&r<=rr) return sum(x);
int mid=l+r>>1,sum=0;
pd(x,l,r);
if(mid>=ll) {
if(r(x)==-1) r(x)=build();
sum+=qry(l(x),ll,rr,l,mid);
}
if(mid<rr) {
if(l(x)==-1) l(x)=build();
sum+=qry(r(x),ll,rr,mid+1,r);
}
pu(x);
return sum;
}
}tree;
int n,m;
int a[N];
signed main() {
tree.root=tree.build();
cin>>n>>m;
for(int i=1;i<=n;i++) {
int x;
cin>>x;
tree.change(tree.root,i,i,1,n,x);
}
while(m--) {
int c,x,y,k;
cin>>c;
if(c==1) {
cin>>x>>y>>k;
tree.change(tree.root,x,y,1,n,k);
}
else {
cin>>x>>y;
cout<<tree.qry(tree.root,x,y,1,n)<<endl;
}
}
return 0;
}
//动态开点
这么牛😀,那我们是不是可以拿线段树实现平衡树的一部分功能呢?
具体的参考洛谷 P3369【模板】普通平衡树。
我们维护一颗值域线段树,对于操作 1~3 是容易的,对于 4 操作,我们可以套个二分来 \(O(\log^2 V)\) 查询,不过如果在线段树上二分就可以 \(O(\log V)\)。对于 5、6 操作,我们只需要做 3 操作之后再做 4 操作即可。
这样是 \(O(n\log^2 V)\) 的😋,如果线段树上二分就可以 \(O(n\log V)\)😍。
这里不介绍例题,因为动态开点已经变成一个功能了🤓。
线段树的合并与分裂
合并:
可能对于两颗线段树,我们有合并信息的需要。
有人可能会说,这难道不是 \(O(n\log n)\) 的吗🐥?
但是如果我们合并的是两颗动态开点线段树,就有可能节点不满🤓,这时候只遍历加入的树上具有的节点即可,比如树 \(A+B\) 只考虑 \(A\) 或 \(B\) 上有的节点即可😎。
具体思想就是这样,对于两颗线段树(可能节点不满),在合并过程中只遍历两颗树中任意一棵树有的点🥵。
我们以雨天的尾巴为例😎。
在这题中,我们对于每种粮食做树上差分🥵,这样每棵树上存的就是一个数组。这时候我们暴力合并这个数组是耗时的🤡,考虑到这个数组有些位置从未涉及过(为 \(0\))🤯,如果使用动态开点线段树维护这个数组,就会省去合并受空节点影响的点😨,这里合并的算法就是线段树合并✍✍✍。
下面给出代码👌
// Problem: P4556 [Vani有约会] 雨天的尾巴 /【模板】线段树合并
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P4556
// Memory Limit: 500 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
#define upp(a, x, y) for (int a = x; a <= y; a++)
#define dww(a, x, y) for (int a = x; a >= y; a--)
#define pb(x) push_back(x)
#define endl '\n'
#define x first
#define y second
#define PII pair<int, int>
using namespace std;
const int N = 1e7 + 10, M = 4e5 + 10;
int ans[M], h[M], ne[M], e[M], final_ans[M], idx;
int st[M],fa[M][21],dep[M],siz[M];
int n, m;
void add(int a, int b) {
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
void init() {
dep[1] = 1;
queue<int> qq; qq.push(1);
while (qq.size()) {
auto iter = qq.front();
qq.pop();
for (int i = h[iter]; i != -1; i = ne[i]) {
int j = e[i];
if (dep[j]) continue;
dep[j] = dep[iter] + 1;
fa[j][0] = iter;
upp(k, 1, 20) fa[j][k] = fa[fa[j][k - 1]][k - 1];
qq.push(j);
}
}
}
int lca(int a, int b) {
if (dep[a] < dep[b]) swap(a, b);
dww(i, 20, 0) {
if (dep[fa[a][i]] >= dep[b]) {
a = fa[a][i];
}
}
if (a == b) return a;
dww(i, 20, 0) {
if (fa[a][i] != fa[b][i]) {
a = fa[a][i];
b = fa[b][i];
}
}
return fa[a][0];
}
struct node {
int maxn, pl, l, r;
#define maxn(x) tr[x].maxn
#define pl(x) tr[x].pl
#define l(x) tr[x].l
#define r(x) tr[x].r
}tr[N];
int root[M];
int tot;
void pu(int x) {
if (maxn(l(x)) >= maxn(r(x))) {
maxn(x) = maxn(l(x));
pl(x) = pl(l(x));
}
else {
maxn(x) = maxn(r(x));
pl(x) = pl(r(x));
}
}
void change(int &x, int l, int r, int p, int k) {
if (!x) x = ++tot;
if (l == r) {
maxn(x) += k;
pl(x) = l;
return;
}
int mid = l + r >> 1;
if (p <= mid) change(l(x), l, mid, p, k);
else change(r(x), mid + 1, r, p, k);
pu(x);
}
int merge(int p, int q, int l, int r) {
if (!p) return q;
if (!q) return p;
if (l == r) {
maxn(p) += maxn(q);
return p;
}
int mid = l + r >> 1;
l(p) = merge(l(p), l(q), l, mid);
r(p) = merge(r(p), r(q), mid + 1, r);
pu(p);
return p;
}
void dfs(int u, int fa) {
for (int i = h[u]; i != -1; i = ne[i]) {
int j = e[i];
if (j == fa) continue;
dfs(j, u);
root[u]=merge(root[u], root[j], 1, 1e5);
}
if (maxn(root[u]) <= 0) final_ans[u] = 0;
else final_ans[u] = pl(root[u]);
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
memset(h, -1, sizeof h);
memset(st, 0, sizeof st);
idx = 0;
tr[0] = { -1, -1, 0, 0 };
cin >> n >> m;
upp(i, 1, n - 1) {
int x, y;
cin >> x >> y;
add(x, y);
add(y, x);
}
init();
upp(i, 1, m) {
int x, y, z; cin >> x >> y >> z;
ans[i]=lca(x, y);
change(root[x], 1, 1e5, z, 1);
change(root[y], 1, 1e5, z, 1);
change(root[ans[i]], 1, 1e5, z, -1);
if (ans[i] != 1) change(root[fa[ans[i]][0]], 1, 1e5, z, -1);
}
dfs(1, -1);
upp(i, 1, n) cout << final_ans[i] << endl;
return 0;
}
分裂:
有合并就有分裂😈😈😈,简单来说,就是从一棵树里分裂几个叶子节点出去(非叶子节点受到影响)🤓。

变成:
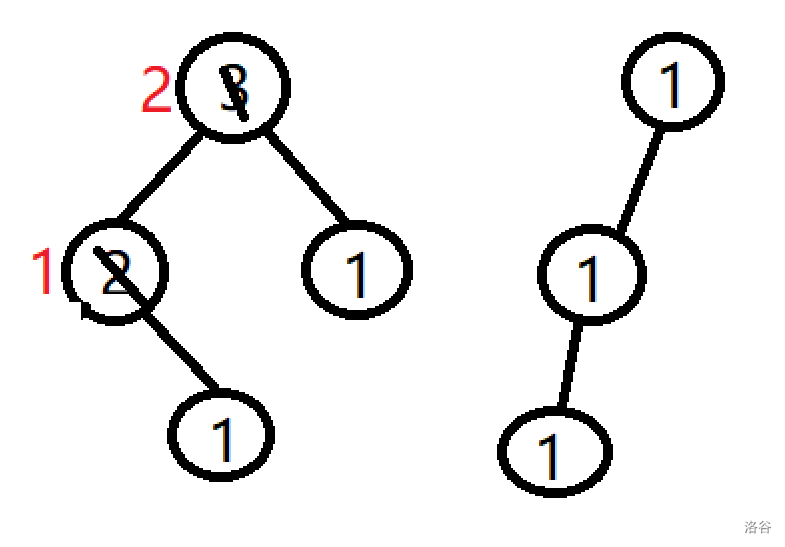
对于所有的操作,均摊时间和空间复杂度不会超过 \(O(\log V)\)👀。值得注意的是🤓,我们在上文线段树合并中没有使用回收节点,但是在线段树分裂的代码中使用了,此时我们回收节点可能可以方便后面创捷节点👁🗨。
// Problem: P5494 【模板】线段树分裂
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P5494
// Memory Limit: 128 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
#define int long long
#define upp(a, x, y) for (int a = x; a <= y; a++)
#define dww(a, x, y) for (int a = x; a >= y; a--)
#define pb(x) push_back(x)
#define endl '\n'
#define x first
#define y second
#define PII pair<int, int>
using namespace std;
const int N = 4e6 + 10;
int n, m;
struct node {
int lson, rson, sum;
#define lson(x) tr[x].lson
#define rson(x) tr[x].rson
#define sum(x) tr[x].sum
} tr[N];
int reuse[N], rtop, idx;
int root[N], rt;
int getnew() {
if (rtop) return reuse[rtop--];
return ++idx;
}
void del(int x) {
reuse[++rtop] = x;
lson(x) = rson(x) = sum(x) = 0;
}
void pu(int x) { sum(x) = sum(lson(x)) + sum(rson(x)); }
void change(int &x, int l, int r, int p, int k) {
if (!x) x = getnew();
if (l == r) {
sum(x) += k;
return;
}
int mid = l + r >> 1;
if (p <= mid)
change(lson(x), l, mid, p, k);
else
change(rson(x), mid + 1, r, p, k);
pu(x);
}
int qry(int x, int l, int r, int ll, int rr) {
if (!x) return 0;
if (l >= ll && r <= rr) return sum(x);
int mid = l + r >> 1, sum = 0;
if (ll <= mid) sum += qry(lson(x), l, mid, ll, rr);
if (rr > mid) sum += qry(rson(x), mid + 1, r, ll, rr);
return sum;
}
int kth(int x, int l, int r, int k) {
if (l == r) return l;
int mid = l + r >> 1;
if (k > sum(lson(x))) return kth(rson(x), mid + 1, r, k - sum(lson(x)));
return kth(lson(x), l, mid, k);
}
int merge(int p, int q) {
if (!p || !q) return p + q;
sum(p) += sum(q);
lson(p) = merge(lson(p), lson(q));
rson(p) = merge(rson(p), rson(q));
del(q);
return p;
}
void split(int p, int &q, int k) {
if (!p) return;
int v = sum(lson(p));
q = getnew();
if (k > v)
split(rson(p), rson(q), k - v);
else
swap(rson(p), rson(q));
if (k < v) split(lson(p), lson(q), k);
sum(q) = sum(p) - k;
sum(p) = k;
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
rt = 1;
upp(i, 1, n) {
int x;
cin >> x;
change(root[rt], 1, n, i, x);
}
upp(i, 1, m) {
int op, x, y, z, tmp = 0;
cin >> op;
if (op == 0) {
cin >> x >> y >> z;
rt++;
int s1 = qry(root[x], 1, n, 1, z), s2 = qry(root[x], 1, n, y, z);
split(root[x], root[rt], s1 - s2);
split(root[rt], tmp, s2);
root[x] = merge(root[x], tmp);
} else if (op == 1) {
cin >> x >> y;
root[x] = merge(root[x], root[y]);
} else if (op == 2) {
cin >> x >> y >> z;
change(root[x], 1, n, z, y);
} else if (op == 3) {
cin >> x >> y >> z;
cout << qry(root[x], 1, n, y, z) << endl;
} else if (op == 4) {
int x, y;
cin >> x >> y;
if (y > sum(root[x]))
cout << -1 << endl;
else {
cout << kth(root[x], 1, n, y) << endl;
}
}
}
return 0;
}
例题一
P3224 [HNOI2012] 永无乡
首先建桥可以线段树合并,为了维护根,我们使用并查集来合并两个总根,查询时查询总根的答案就行了🍞。
// Problem: P3224 [HNOI2012] 永无乡
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3224
// Memory Limit: 512 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
#define int long long
#define upp(a, x, y) for (int a = x; a <= y; a++)
#define dww(a, x, y) for (int a = x; a >= y; a--)
#define pb(x) push_back(x)
#define endl '\n'
#define x first
#define y second
#define PII pair<int, int>
using namespace std;
const int N = 1.4e7 + 10, M = 1e5 + 10;
int n, m, qq;
int a[M];
struct node {
int lson, rson, sum;
#define lson(x) tr[x].lson
#define rson(x) tr[x].rson
#define sum(x) tr[x].sum
} tr[N];
int root[N], rt;
int reuse[N], top, idx;
int p[N];
void init() { upp(i, 1, n) p[i] = i; }
int find(int x) {
if (p[x] == x) return x;
return p[x] = find(p[x]);
}
int getnew() {
if (top) return reuse[top--];
return ++idx;
}
void del(int x) {
reuse[++top] = x;
lson(x) = rson(x) = sum(x) = 0;
}
void pu(int x) { sum(x) = sum(lson(x)) + sum(rson(x)); }
void change(int &x, int p, int k = 1, int l = 1, int r = n) {
if (!x) x = getnew();
if (l == r) return sum(x) = k, void();
int mid = l + r >> 1;
if (p <= mid)
change(lson(x), p, k, l, mid);
else
change(rson(x), p, k, mid + 1, r);
pu(x);
}
int kth(int x, int k, int l = 1, int r = n) {
if (l == r) return l;
int mid = l + r >> 1;
if (k <= sum(lson(x))) return kth(lson(x), k, l, mid);
return kth(rson(x), k - sum(lson(x)), mid + 1, r);
}
int qry(int x, int ll, int rr, int l = 1, int r = n) {
if (!x) return 0;
if (l >= ll && r <= rr) return sum(x);
int mid = l + r >> 1, sum = 0;
if (ll <= mid) sum += qry(lson(x), ll, rr, l, mid);
if (rr > mid) sum += qry(rson(x), ll, rr, mid + 1, r);
return sum;
}
int merge(int p, int q) {
if (p == q) return p;
if (!p || !q) return p + q;
sum(p) += sum(q);
lson(p) = merge(lson(p), lson(q));
rson(p) = merge(rson(p), rson(q));
del(q);
return p;
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
map<int, int> ha;
upp(i, 1, n) {
cin >> a[i];
ha[a[i]] = i;
change(root[i], a[i]);
}
init();
upp(i, 1, m) {
int x, y;
cin >> x >> y;
int fx = find(x), fy = find(y);
p[fy] = fx;
merge(root[fx], root[fy]);
}
cin >> qq;
upp(i, 1, qq) {
char op;
cin >> op;
int x, y;
if (op == 'Q') {
cin >> x >> y;
if (qry(root[find(x)], 1, n) < y)
cout << -1 << endl;
else
cout << ha[kth(root[find(x)], y)] << endl;
} else {
cin >> x >> y;
int fx = find(x), fy = find(y);
p[fy] = fx;
merge(root[fx], root[fy]);
}
}
return 0;
}
例题二
P2824 [HEOI2016/TJOI2016] 排序
我们可以在线维护这题🥵!
考虑权值线段树本来就有性质有序,而将 \([l,r]\) 排序就相当于合并 \([l,r]\) 的所有权值线段树加上增减标签🤩。查询 \(q\) 位置的值则为访问 \(q\) 处的权值线段树最小或者最大的值。
合并区间的代码挺难写的😎,具体的我们用 set 来维护所有根的位置、单调性。用 set 本身自带的单调性来合并,以及用到一部分好的功能🍅。写法来源题解区大佬,这是很好的写法🥶。
// Problem: P2824 [HEOI2016/TJOI2016] 排序
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P2824
// Memory Limit: 256 MB
// Time Limit: 4000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
#define int long long
#define upp(a, x, y) for (int a = x; a <= y; a++)
#define dww(a, x, y) for (int a = x; a >= y; a--)
#define pb(x) push_back(x)
#define endl '\n'
#define x first
#define y second
#define PII pair<int, int>
using namespace std;
const int N = 4e6 + 10, M = 1e5 + 10;
int n, m;
int a[M];
struct node {
int lson, rson, sum;
#define lson(x) tr[x].lson
#define rson(x) tr[x].rson
#define sum(x) tr[x].sum
} tr[N];
int root[N], rev[N], ml[N], mr[N], rt;
int reuse[N], top, idx;
int getnew() {
if (top) return reuse[top--];
return ++idx;
}
void del(int x) {
reuse[++top] = x;
lson(x) = rson(x) = sum(x) = 0;
}
void pu(int x) { sum(x) = sum(lson(x)) + sum(rson(x)); }
void change(int &x, int p, int k = 1, int l = 1, int r = n) {
if (!x) x = getnew();
if (l == r) return sum(x) = k, void();
int mid = l + r >> 1;
if (p <= mid)
change(lson(x), p, k, l, mid);
else
change(rson(x), p, k, mid + 1, r);
pu(x);
}
int kth(int x, int k, int l = 1, int r = n) {
if (l == r) return l;
int mid = l + r >> 1;
if (k <= sum(lson(x))) return kth(lson(x), k, l, mid);
return kth(rson(x), k - sum(lson(x)), mid + 1, r);
}
int qry(int x, int ll, int rr, int l = 1, int r = n) {
if (!x) return 0;
if (l >= ll && r <= rr) return sum(x);
int mid = l + r >> 1, sum = 0;
if (ll <= mid) sum += qry(lson(x), ll, rr, l, mid);
if (rr > mid) sum += qry(rson(x), ll, rr, mid + 1, r);
return sum;
}
int merge(int p, int q) {
if (!p || !q) return p + q;
sum(p) += sum(q);
lson(p) = merge(lson(p), lson(q));
rson(p) = merge(rson(p), rson(q));
del(q);
return p;
}
void split(int p, int &q, int k, int o) {
if (!p) return;
int v;
if (o == 0) {
v = sum(lson(p));
q = getnew();
if (k > v)
split(rson(p), rson(q), k - v, o);
else
swap(rson(p), rson(q));
if (k < v) split(lson(p), lson(q), k, o);
sum(q) = sum(p) - k;
sum(p) = k;
} else {
v = sum(rson(p));
q = getnew();
if (k > v)
split(lson(p), lson(q), k - v, o);
else
swap(lson(p), lson(q));
if (k < v) split(rson(p), rson(q), k, o);
sum(q) = sum(p) - k;
sum(p) = k;
}
}
set<int> pl;
int o[N];
auto sp(int p) {
auto now = pl.lower_bound(p);
if (*now == p) return now;
now--;
split(root[*now], root[p], p - *now, o[p] = o[*now]);
return pl.insert(p).first;
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
pl.insert(n + 1);
upp(i, 1, n) {
int x;
cin >> x;
change(root[i], x);
pl.insert(i);
}
upp(i, 1, m) {
int op, l, r;
cin >> op >> l >> r;
auto il = sp(l), ir = sp(r + 1);
for (auto i = ++il; i != ir; i++) merge(root[l], root[*i]);
o[l] = op;
pl.erase(il, ir);
}
int qq;
cin >> qq;
sp(qq);
sp(qq + 1);
cout << kth(root[qq], qry(root[qq], 1, n)) << endl;
return 0;
}
标记永久化
这个技巧主要用来方便后面写可持久化线段树🤠。
概括的来说,标记永久化就是为线段树省去下传和上传的操作🤣。
对于下传操作,在修改的时候同样的记录标记,我们在询问的函数参数传递标记就行了🦍。
对于上传操作,我们在修改的时候顺便修改父节点的信息就行🤗。
写个线段树 1🧐。
// Problem: P3372 【模板】线段树 1
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3372
// Memory Limit: 512 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
#define int long long
#define upp(a, x, y) for (int a = x; a <= y; a++)
#define dww(a, x, y) for (int a = x; a >= y; a--)
#define pb(x) push_back(x)
#define endl '\n'
#define x first
#define y second
#define PII pair<int, int>
using namespace std;
const int N = 1e5 + 10;
int a[N], n, m;
struct node {
int l, r, sum, tg;
#define l(x) tr[x].l
#define r(x) tr[x].r
#define sum(x) tr[x].sum
#define tg(x) tr[x].tg
};
struct segtree {
node tr[N * 4];
void build(int x, int l, int r) {
l(x) = l, r(x) = r;
if (l == r) return sum(x) = a[l], void();
int mid = l + r >> 1;
build(x * 2, l, mid);
build(x * 2 + 1, mid + 1, r);
sum(x) = sum(x * 2) + sum(x * 2 + 1);
}
void change(int x, int ll, int rr, int k) {
int l = l(x), r = r(x);
sum(x) += (rr - ll + 1) * k;
if (l >= ll && r <= rr) return tg(x) += k, void();
int mid = l + r >> 1;
if (ll <= mid) change(x * 2, ll, min(mid, rr), k);
if (rr > mid) change(x * 2 + 1, max(ll, mid + 1), rr, k);
}
int qry(int x, int ll, int rr, int lz) {
int l = l(x), r = r(x);
if (l >= ll && r <= rr) return sum(x) + (r - l + 1) * lz;
int mid = l + r >> 1, sum = 0;
if (ll <= mid) sum += qry(x * 2, ll, rr, lz + tg(x));
if (rr > mid) sum += qry(x * 2 + 1, ll, rr, lz + tg(x));
return sum;
}
} t1;
signed main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
upp(i, 1, n) cin >> a[i];
t1.build(1, 1, n);
upp(i, 1, m) {
int op, x, y, z;
cin >> op;
if (op == 1) {
cin >> x >> y >> z;
t1.change(1, x, y, z);
} else {
cin >> x >> y;
cout << t1.qry(1, x, y, 0) << endl;
}
}
return 0;
}
可持久化
实际上,我们每次修改最多影响的节点是 \(O(\log n)\) 的,因此我们如果每次把受影响的节点都复制一份在修改,保持原来的不变。就可以实现访问任意时刻的线段树,一共会开 \(O(n+m \log n)\) 的节点。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号