矩阵快速幂

先从例题引入。

题目

思路

首先你需要知道这是一道板题，由于题目中 \(n\le 10^9\) 所以你需要使用矩阵乘法来加速递推。

目前个人总结的矩乘的步骤：

1.考虑所求内容以及想要推得所求内容需要的其它量，将它们列为一个一行的矩阵。

2.考虑内容之间的联系，设计转移矩阵，每一列的所有行表示，对于那列的量，每个量的转移所需。

3.验证是否正确。

举个例子，如题目要求求斐波那契的第 \(n\) 项，考虑斐波那契的递推式：

\[\begin{aligned} f_{i}=f_{i-1}+f_{i-2}(i>2) \end{aligned} \]

我们发现，如果需要推出第 \(n\) 项，就只要知道 \(n-1\) 与 \(n-2\) 项。所以考虑设计状态矩阵为 \([f_{i},f_{i-1}]\)。

然后考虑内容之间的联系，对于 \(f_{i}\) 我们需要加上原来的 \(f_{i}\) 与 \(f_{i-1}\)，对于 \(f_{i-1}\) 就等于原来的 \(f_{i}\)，所以转移矩阵如下：

\[\begin{aligned} \begin{bmatrix} 1&1\\ 1&0 \end{bmatrix} \end{aligned} \]

然后先预处理一开始 \(i=2\) 的矩阵 \(A\)，答案就是 \(A^{n-2}\) 的 \(f_{i}\)。

对于矩乘结合律的证明：

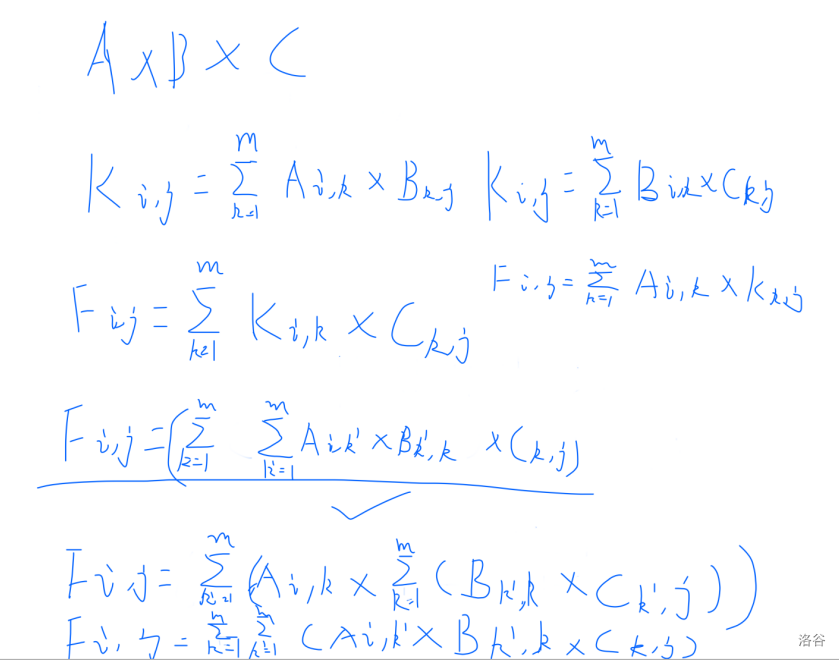
Code

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=4,P=10000;
struct matrix {
	int n,m;
	int a[N][N];
};
matrix operator*(matrix a,matrix b) {
	if(b.n<a.n) swap(a,b);
	matrix c;c.n=min(a.n,b.n),c.m=min(b.m,a.m);
	memset(c.a,0,sizeof c.a);
	for(int i=1;i<=min(a.n,b.n);i++)
		for(int j=1;j<=min(a.m,b.m);j++)
			for(int k=1;k<=a.m;k++)
				c.a[i][j]=(c.a[i][j]+a.a[i][k]*b.a[k][j]%P)%P;
	return c;
}
matrix qmi(matrix a,int b) {
	b--;
	matrix c;
	c.n=a.n,c.m=a.m;
	for(int i=1;i<=c.n;i++)
		for(int j=1;j<=c.m;j++)
			c.a[i][j]=a.a[i][j];
	while(b) {
		if(b&1) c=c*a;
		a=a*a;
		b>>=1;
	}
	return c;
}
signed main() {
	int n;
	while(cin>>n,n!=-1) {
		if(n==0) puts("0");
		else if(n==1) puts("1");
		else if(n==2) puts("1");
		else {
			matrix a,b,c;
			a.n=1,a.m=2,b.n=2,b.m=2;
			memset(a.a,0,sizeof a.a);
			memset(b.a,0,sizeof b.a);
			a.a[1][1]=a.a[1][2]=1;b.a[1][1]=b.a[1][2]=b.a[2][1]=1;
			cout<<(qmi(b,n-2)*a).a[1][1]<<endl;
		}
	}
}