笛卡尔树 学习笔记

简介

笛卡尔树是一种特殊的二叉树，处理一些序列问题
有一些二元组\(k,w\)，那么如果对他们建出一棵树来，满足\(k\)满足\(BST\)性质，\(w\)满足堆性质，那么就是一颗笛卡尔树
容易发现\(treap\)就是一种特殊的笛卡尔树，只不过他是平衡的
通常情况下笛卡尔树不保证平衡，所以不能作为平衡树维护东西，但由于它形态唯一，所以可以用来解决一些序列问题
一般当题目出现区间最值时，或者明显具有笛卡尔树性质时可以考虑这个方向

构建

用单调栈有\(O(n)\)，板子来源于wiki，养生选手懒人stl

for(int i=1;i<=n;i++)
{	
	int p=0;
	while(s.size()&&a[s.top()]>a[i])p=s.top(),s.pop();
	if(s.size())rs[s.top()]=i;
	if(p)ls[i]=p;s.push(i);
}

这里是小根堆，大根堆是小于号
建出来之后栈底元素就是树根

HDU4125

这个比较裸基本是板子，要求权值满足\(BST\),下标满足小根堆，重新排序就好
建完树之后中序遍历的欧拉序就是答案，随便哈希匹配一下就行

HDU6305

将题目中的条件转化为笛卡尔树上的条件
会发现RMQ相似就是笛卡尔树同构，所以求同构的概率
对于一个节点它必须成为子树中的最大值，那么概率就是\(\frac {1}{sz[x]}\),所有点的概率乘在一起就是树同构的概率
而随机变量的期望值是\(\frac{1}{2}\),所以答案就是\(\frac{n}{2\prod sz[x]}\)

SPOJ2616/P6453

经典的笛卡尔树dp题
建小根堆笛卡尔树，这样就可以划分子问题，儿子之间相互独立互不影响
首先\(n*m\)棋盘放\(k\)个车答案是\(\dbinom{n}{k}\times \dbinom{m}{k} \times k!\)
设\(f_{x,i}\)表示在\(x\)子树对应的区间内放了\(i\)个的方案数，考虑树上背包做
先把子树合并起来，这个比较简单
然后统计当前这个区间自己的答案，相当于在最底下再放，枚举子树中放了多少个

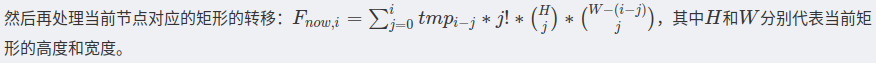
减去的原因也好理解，就是已经放了的列不能再放
注意不能相互覆盖，还有组合数要处理到值域\(10^6\)

HDU6854

为啥都是HDU啊
这个栈中元素个数实际上就是在全局笛卡尔树上以这个点为右子树的点的数量，可以手玩
所以可以做一个dp来求对应笛卡尔树的形态
注意到如果以序列下标作为\(k\)的笛卡尔树的一个子树表示原序列的一个区间，所以区间dp
\(f_{i,j,k}\)表示从\(i\)到\(j\)，以根节点为右子树的点数量是\(k\)的方案数，那么转移就是

\[f_{i,j,k}=\sum_{p=i}^jf_{i,p-1,k}\times f_{p+1,j,k} \times \dbinom{j-i}{p-i} \]

枚举中间的点，把一部分分给左子树另一部分分给右子树，算套路了，然后乘上组合数贡献
注意这里如果\(a_p\)是-1的话那么\(k\)随便枚举，否则只能是\(a_p\),复杂度\(n^3\)

还有道ZJOI，咕了

总结

这类题目大部分都是先建树，将原条件转化到树上，简单点直接dfs就可以，复杂一点要树形dp
还有就是反过来，不建树，而是根据树的特点做计数之类，设计对应的dp方程