模拟55 考试总结
考试经过
开题一看:NOI模拟,人傻了
于是在不懈努力之下冲了四个暴力,预计30+20+30+20=100
实际:0+10+0+0=10
T1五分钟推出来dp结果没处理边界挂30
T2剪了半天枝结果没判无解挂成和puts("-1")一个分
T3十分钟冲上顺利爆零
T4最后一分钟看出来写假了然并卵
四个挂了三个,萎+=inf
T1. Skip
首先有一个比较简单的dp:设\(f_i\)表示他最后参加地\(i\)场比赛最优值,就有
如果不考虑只能选递增的限制的话应该是一个斜率优化菜鸡一下午才学会这是啥,变形
然后就是维护一个左下凸包,理论上直接单调队列就行
然而他对权值有限制,必须递增,大佬都用的cdq,太菜不会
一个被认为套路的东西:线段树维护凸包
对权值离散化,每个节点保存一个单调队列,存这个节点表示的区间里的斜率,每次在一条链都插入对应的\(f_j-(\frac{j^2+j}{2})\),然后弹队尾,由于\(i\)单调,所以队头直接是最优决策,查询时在每个区间内查询即可,基本和线段树一样,单调队列一次操作均摊\(O(1)\),总复杂度\(n\log n\)
由于stl的deque比较慢,所以似乎不是很快,但复杂度是正确的
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=100050;
int f[N],a[N],w[N],lsh[N];
int sum1[N],sum2[N];
struct tree{
int l,r;deque <pair<int,int> > q;
}tr[4*N];
void build(int id,int l,int r)
{
tr[id].l=l;tr[id].r=r;
if(l==r)return;
int mid=(l+r)>>1;
build(id*2,l,mid);build(id*2+1,mid+1,r);
}
inline double gan(pair<int,int> x,pair<int,int> y)
{
return ((double)y.second-x.second)/((double)y.first-x.first);
}
void add(int id,int p,pair<int,int> v)
{
while(tr[id].q.size()>=2&&gan(tr[id].q[tr[id].q.size()-2],tr[id].q[tr[id].q.size()-1])<gan(tr[id].q[tr[id].q.size()-1],v))tr[id].q.pop_back();
tr[id].q.push_back(v);if(tr[id].l==tr[id].r)return;
int mid=(tr[id].l+tr[id].r)>>1;
if(p<=mid)add(id*2,p,v);else add(id*2+1,p,v);
}
inline int get(int id,int l,int r,int i)
{
if(l<=tr[id].l&&r>=tr[id].r)
{
while(tr[id].q.size()>=2&&gan(tr[id].q[0],tr[id].q[1])>(-1.0)*i)tr[id].q.pop_front();
if(!tr[id].q.size())return -1e9;
return i*tr[id].q.front().first+tr[id].q.front().second;
}
int mid=(tr[id].l+tr[id].r)>>1;
if(r<=mid)return get(id*2,l,r,i);
if(l>mid)return get(id*2+1,l,r,i);
return max(get(id*2,l,mid,i),get(id*2+1,mid+1,r,i));
}
signed main()
{
freopen("skip.in","r",stdin);
freopen("skip.out","w",stdout);
memset(f,128,sizeof(f));
int n;cin>>n;
for(int i=1;i<=n;i++)scanf("%lld",&w[i]);
for(int i=1;i<=n;i++)lsh[i]=w[i];
sort(lsh+1,lsh+n+1);
int cnt=unique(lsh+1,lsh+n+1)-lsh-1;
for(int i=1;i<=n;i++)a[i]=lower_bound(lsh+1,lsh+cnt+1,w[i])-lsh;
a[0]=-1e9;a[n+1]=cnt+1;//w[n+1]=0;
for(int i=1;i<=n+1;i++)sum1[i]=(i-i*i)/2,sum2[i]=(i*i+i)/2;
build(1,0,cnt+1);add(1,0,make_pair(0,0));
for(int i=1;i<=n+1;i++)
{
f[i]=get(1,0,a[i],i)+w[i]+sum1[i];
add(1,a[i],make_pair(i,f[i]-sum2[i]));
}
cout<<f[n+1]<<endl;
return 0;
}
代码粘过来似乎有点问题
记得特殊处理一下边界
貌似是第一道凸包题……
T2.String
不会,咕
T3. Permutation
upd on 9.17
这个题似乎打表很多分,然而这都没想到,只能复刻题解
首有这么一个东西
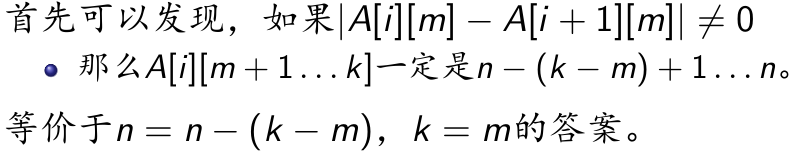
意思是,如果后面还有数没有选,那么一定存在仍然选\(m\)而后面选更大的方案使得字典序更大
于是就变成了考虑\(n=n-(k-m),m=k\)的情况
然后分类讨论,看\(A_{i,1},A_{i+1,1}\)的大小关系
首先考虑\(A_{i,1}+1=A_{i+1,1}\)的情况
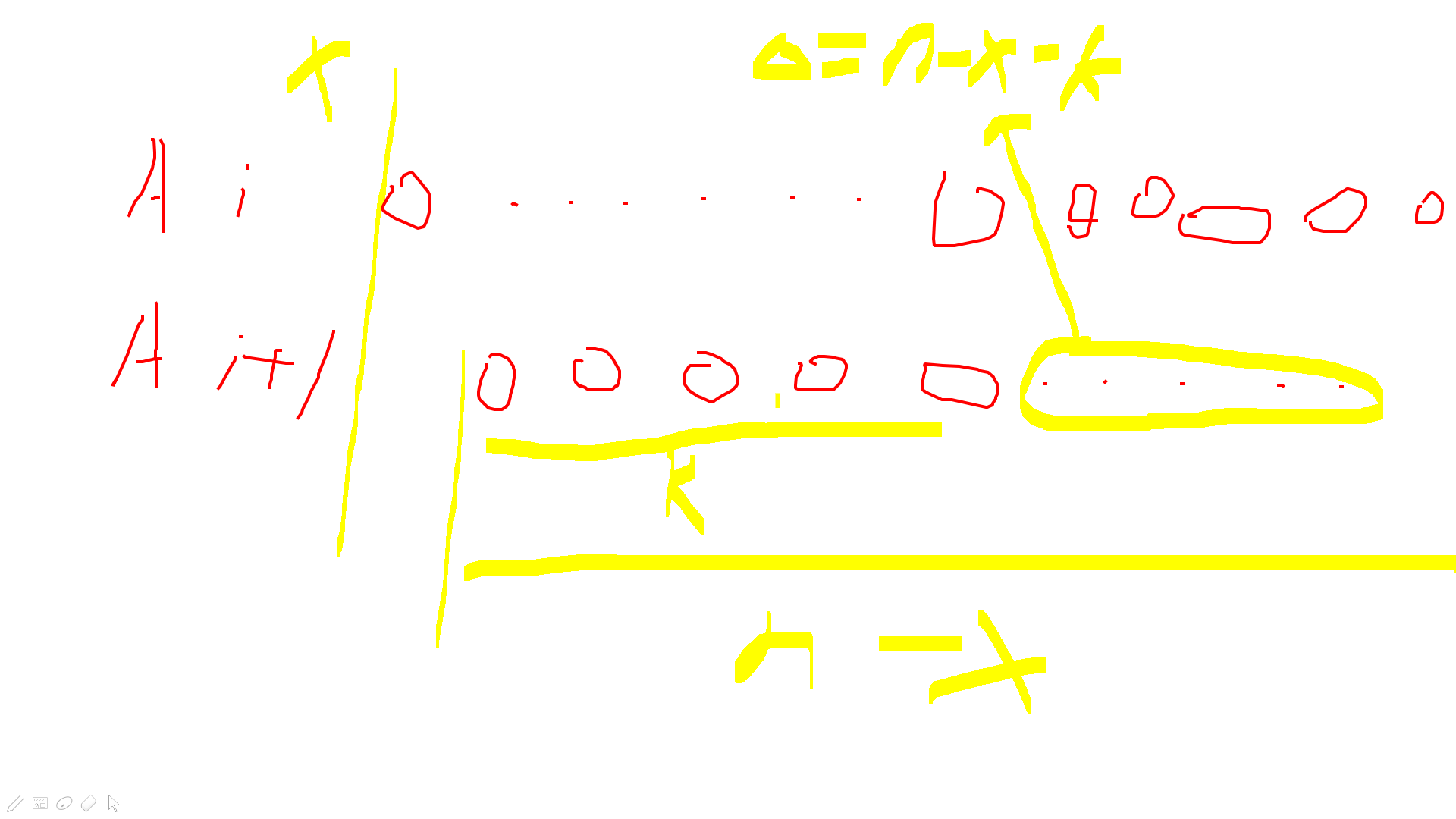
重新排就意味着前面连续,可以枚举第一个数\(x\)的取值算出答案,这部分答案就是
考虑剩下的情况,\(A_{i,1}=A_{i+1,1}\),这样可以递归划分子问题,如果设答案为\(f_{n,k}\)的话,那么这部分贡献就是
总的来说就是\(f_{n,k}=\dbinom{n-k}{2}+\sum_{j=1}^{n-(k-1)}f_{n-j,k-1}\),现在已经可以\(n^2\)了
考虑式子的实际意义,这就有了一个很神奇的东西:整数划分
我们借鉴一下工业题的思想,看能不能一次算出每个\(g\)的贡献系数,然后用某种方式合并
由于\(g_{n,k}=\dbinom{n-k}{2}\),所以可以视为将\(n-k+1\)分成3个数的方案,推广
试图计算一个\(g_{m,q}\)对答案\(f_{n,k}\)的贡献
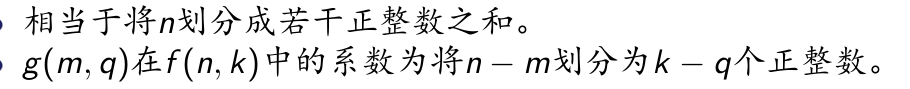
这个比较类似于网格上从一个点走到另一个点的方案数
或者也可以考虑一个\(g\)对应一个\(f\),就是之间有多少个\(f\)就是贡献多少次,抽象就是整数划分
那么一个的贡献就是\(\dbinom{n-m+1}{k-q-1}\)
如果你前一维\(m\)枚举的话,就是
似乎是组合恒等式,所以答案就是\(\dbinom{k-q-2}{n-q}\)
注意特殊处理第一行(q=1),因为这时\(g\)不满足刚才的意义和式子,而是\(m-1\),所以特殊处理,系数当然还是一样
核心代码只有两行
for(int i=2;i<=k;i++)ans=(ans+C(n-i,k-i+2))%mod;
for(int i=1;i<=n;i++)ans=(ans+(i-1)*C(n-i-1,k-2)%mod)%mod;
还要注意如果\(k\)本来就是1,需要特判,答案显然只有\(n-1\)
完整代码
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=1000050;
const int mod=1e9+7;
int inv[N],jc[N],jcny[N];
int n,k,m;
inline int C(int x,int y)
{
if(x<y||y<0)return 0;
if(x<y)return 0;
if(!y)return 1;
return jc[x]*jcny[y]%mod*jcny[x-y]%mod;
}
signed main()
{
freopen("perm.in","r",stdin);
freopen("perm.out","w",stdout);
cin>>n>>k>>m;
jc[0]=jc[1]=inv[1]=jcny[0]=jcny[1]=1;
for(int i=2;i<=n+30;i++)
{
jc[i]=jc[i-1]*i%mod;
inv[i]=(mod-mod/i)*inv[mod%i]%mod;
jcny[i]=jcny[i-1]*inv[i]%mod;
}
int ans=0;n-=(k-m);k=m;
if(k==1){cout<<n-1<<endl;return 0;}
for(int i=2;i<=k;i++)ans=(ans+C(n-i,k-i+2))%mod;
for(int i=1;i<=n;i++)ans=(ans+(i-1)*C(n-i-1,k-2)%mod)%mod;
cout<<ans<<endl;
return 0;
}
这道题其实很好,尤其是对于组合数学这一块,变成分整数是很好的一种思路,但不是太好理解,必要的时候可以结合实际意义解释
观察性质这一块做的好像也不是特别好,还要努力
T4.小P的生成树
其实是高考数学题。。。
结论是如果和的模最大的话,那么把和的方向的单位向量作为基底,按每个向量在他这个方向的投影长做一遍最大生成树就行
然而方向向量看似很多不可能全部枚举然而你只要卡到0.05弧度就A了
发现一个性质:最大生成树的形态只和边权相对大小有关系
因为每两个向量对一个向量投影,那么在半圈内大小相对关系都是不变的
于是预处理出所有这样的区间,每个区间之内所有向量投影相对大小不变,随便选一个作为方向向量做一遍,最后取最大值
复杂度\(m^3\log m\)
#include <bits/stdc++.h>
using namespace std;
const int N=205;
const double exs=1e-10;
inline bool pd(double xx,double yy)
{
if(xx>yy)swap(xx,yy);
if(yy-xx<exs)return 1;
return 0;
}
const double pie=acos(-1.0);
struct node{
int from,to,next,wa,wb;
double ww;
friend bool operator<(node x,node y)
{
return x.ww<y.ww;
}
}a[2*N];
int head[N],mm=1;
inline void add(int x,int y,int wa,int wb)
{
a[mm].from=x;a[mm].to=y;
a[mm].wa=wa;a[mm].wb=wb;
a[mm].next=head[x];head[x]=mm++;
}
vector <double> du;int n,m;
priority_queue <node> q;
int fa[N];
inline int find(int x)
{
if(fa[x]!=x)fa[x]=find(fa[x]);
return fa[x];
}
inline double gan()
{
for(int i=1;i<mm;i+=2)q.push(a[i]);
for(int i=1;i<=n;i++)fa[i]=i;
int an1=0,an2=0;
while(q.size())
{
int x=q.top().from,y=q.top().to;
int wa=q.top().wa,wb=q.top().wb;q.pop();
int fx=find(x),fy=find(y);
if(fx==fy)continue;
an1+=wa,an2+=wb;
fa[fx]=fy;
}
return sqrt((double)an1*an1+(double)an2*an2);
}
signed main()
{
freopen("mst.in","r",stdin);
freopen("mst.out","w",stdout);
cin>>n>>m;
for(int i=1;i<=m;i++)
{
int x,y,wa,wb;scanf("%d%d%d%d",&x,&y,&wa,&wb);
add(x,y,wa,wb);add(y,x,wa,wb);
}
for(int i=1;i<mm;i+=2)
{
int x=a[i].wa,y=a[i].wb;
for(int j=i+2;j<mm;j+=2)
{
int xx=a[j].wa,yy=a[j].wb;
if(y==yy)
{
du.push_back(0.5*pie);du.push_back(1.5*pie);
continue;
}
double du1=atan((double)(x-xx)/(double)(yy-y));
double du2=du1+pie;
du.push_back(du1);du.push_back(du2);
}
}
sort(du.begin(),du.end());
double ans=-1e9;
for(int i=0;i<du.size()-1;i++)
{
double p1=du[i],p2=du[i+1];
double p=(p1+p2)/2.0;
for(int j=1;j<mm;j++)
{
double wa=a[j].wa,wb=a[j].wb;
a[j].ww=wa*cos(p)+wb*sin(p);
}
ans=max(ans,gan());
}
printf("%.6lf",ans);
return 0;
}
考试总结
考了一个月终于垫底了
不细是最大的问题,挂分只能证明自己实力不济
把题读完,把代码打好,把暴力冲满
正解的话不能强求,但打表的分还是应该有
还发现一点,的确没有什么题不可做,感觉一直学不会的凸包整了一下午也就差不多了
接受,然后去改变.
Accepted.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号