树链剖分模板

【模板】重链剖分/树链剖分

题目描述

如题，已知一棵包含 \(N\) 个结点的树（连通且无环），每个节点上包含一个数值，需要支持以下操作：

• 1 x y z，表示将树从 \(x\) 到 \(y\) 结点最短路径上所有节点的值都加上 \(z\)。

• 2 x y，表示求树从 \(x\) 到 \(y\) 结点最短路径上所有节点的值之和。

• 3 x z，表示将以 \(x\) 为根节点的子树内所有节点值都加上 \(z\)。

• 4 x 表示求以 \(x\) 为根节点的子树内所有节点值之和

输入格式

第一行包含 \(4\) 个正整数 \(N,M,R,P\)，分别表示树的结点个数、操作个数、根节点序号和取模数（即所有的输出结果均对此取模）。

接下来一行包含 \(N\) 个非负整数，分别依次表示各个节点上初始的数值。

接下来 \(N-1\) 行每行包含两个整数 \(x,y\)，表示点 \(x\) 和点 \(y\) 之间连有一条边（保证无环且连通）。

接下来 \(M\) 行每行包含若干个正整数，每行表示一个操作。

输出格式

输出包含若干行，分别依次表示每个操作 \(2\) 或操作 \(4\) 所得的结果（对 \(P\) 取模）。

样例 #1

样例输入 #1

5 5 2 24
7 3 7 8 0 
1 2
1 5
3 1
4 1
3 4 2
3 2 2
4 5
1 5 1 3
2 1 3

样例输出 #1

2
21

提示

【数据规模】

对于 \(30\%\) 的数据： \(1 \leq N \leq 10\)，\(1 \leq M \leq 10\)；

对于 \(70\%\) 的数据： \(1 \leq N \leq {10}^3\)，\(1 \leq M \leq {10}^3\)；

对于 \(100\%\) 的数据： \(1\le N \leq {10}^5\)，\(1\le M \leq {10}^5\)，\(1\le R\le N\)，\(1\le P \le 2^{31}-1\)。

【样例说明】

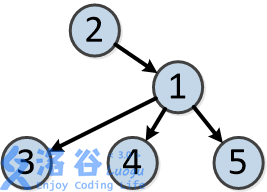
树的结构如下：

各个操作如下：

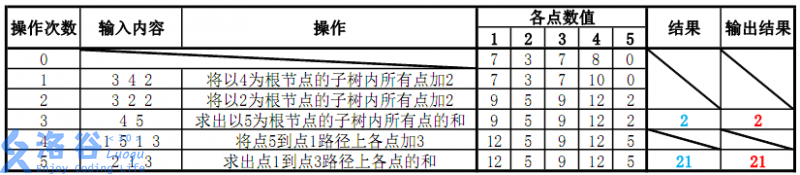
故输出应依次为 \(2\) 和 \(21\)。

深度理解：
https://www.cnblogs.com/zwfymqz/p/8094500.html

点击查看代码

#include<bits/stdc++.h>
using namespace std;
const int MAXN=2*1e6+10;
inline char nc() {
	static char buf[MAXN],*p1=buf,*p2=buf;
	return p1==p2&&(p2=(p1=buf)+fread(buf,1,MAXN,stdin),p1==p2)?EOF:*p1++;
}
inline int read() {
	char c=nc();
	int x=0,f=1;
	while(c<'0'||c>'9') {
		if(c=='-')f=-1;
		c=nc();
	}
	while(c>='0'&&c<='9') {
		x=x*10+c-'0',c=nc();
	}
	return x*f;
}
struct Tree {
	int u,to,nxt;
} edge[MAXN];
int head[MAXN];
int num=1;
struct SegTree {
	int l,r,w,add;
} tr[MAXN];
int N,M,root,MOD,cnt=0,a[MAXN],b[MAXN];
inline void AddEdge(int u,int v) {
	num++;
	edge[num].to=v;
	edge[num].nxt=head[u];
	head[u]=num;
}
int dep[MAXN],fa[MAXN],son[MAXN],siz[MAXN],top[MAXN],idx[MAXN];
void dfs1(int u,int fat,int depth) {
	dep[u]=depth;
	fa[u]=fat;
	siz[u]=1;
	int maxson=-1;
	for(int i=head[u]; i; i=edge[i].nxt) {
		int v=edge[i].to;
		if(v==fat) continue;
		dfs1(v,u,depth+1);
		siz[u]+=siz[v];
		if(siz[v]>maxson)maxson=siz[v],son[u]=v;
	}
}
void pushup(int p) {
	tr[p].w=(tr[p<<1].w+tr[p<<1|1].w+MOD)%MOD;
}
void Build(int p,int l,int r) {
	tr[p].l=l;
	tr[p].r=r;
	if(l==r) {
		tr[p].w=a[l];
		return ;
	}
	int mid=(l+r)>>1;
	Build(p<<1,l,mid);
	Build(p<<1|1,mid+1,r);
	pushup(p);
}
void dfs2(int u,int topf) {
	idx[u]=++cnt;
	a[cnt]=b[u];
	top[u]=topf;
	if(!son[u]) return ;
	dfs2(son[u],topf);
	for(int i=head[u]; i; i=edge[i].nxt)
		if(!idx[edge[i].to])
			dfs2(edge[i].to,edge[i].to);
}
void pushdown(int p) {
	if(!tr[p].add) return ;
	tr[p<<1].w=(tr[p<<1].w+(tr[p<<1].r-tr[p<<1].l+1)*tr[p].add)%MOD;
	tr[p<<1|1].w=(tr[p<<1|1].w+(tr[p<<1|1].r-tr[p<<1|1].l+1)*tr[p].add)%MOD;
	tr[p<<1].add=(tr[p<<1].add+tr[p].add)%MOD;
	tr[p<<1|1].add=(tr[p<<1|1].add+tr[p].add)%MOD;
	tr[p].add=0;
}
void IntervalAdd(int p,int l,int r,int val) {
	if(l<=tr[p].l&&tr[p].r<=r) {
		tr[p].w+=(tr[p].r-tr[p].l+1)*val;
		tr[p].add+=val;
		return ;
	}
	pushdown(p);
	int mid=(tr[p].l+tr[p].r)>>1;
	if(l<=mid)IntervalAdd(p<<1,l,r,val);
	if(r>mid)IntervalAdd(p<<1|1,l,r,val);
	pushup(p);
}
void TreeAdd(int x,int y,int val) {
	while(top[x]!=top[y]) {
		if(dep[top[x]]<dep[top[y]])swap(x,y);
		IntervalAdd(1,idx[top[x]],idx[x],val);
		x=fa[top[x]];
	}
	if(dep[x]>dep[y])swap(x,y);
	IntervalAdd(1,idx[x],idx[y],val);
}
int IntervalSum(int p,int l,int r) {
	int ans=0;
	if(l<=tr[p].l&&tr[p].r<=r)
		return tr[p].w;
	pushdown(p);
	int mid=(tr[p].l+tr[p].r)>>1;
	if(l<=mid)ans=(ans+IntervalSum(p<<1,l,r))%MOD;
	if(r>mid)ans=(ans+IntervalSum(p<<1|1,l,r))%MOD;
	return ans;
}
int TreeSum(int x,int y) {
	int ans=0;
	while(top[x]!=top[y]) {
		if(dep[top[x]]<dep[top[y]])swap(x,y);
		ans=(ans+IntervalSum(1,idx[top[x]],idx[x]))%MOD;
		x=fa[top[x]];
	}
	if(dep[x]>dep[y])swap(x,y);
	ans=(ans+IntervalSum(1,idx[x],idx[y]))%MOD;
	return ans;
}
int main() {
	N=read();
	M=read();
	root=read();
	MOD=read();
	for(int i=1; i<=N; i++) b[i]=read();
	for(int i=1; i<=N-1; i++) {
		int x=read(),y=read();
		AddEdge(x,y);
		AddEdge(y,x);
	}
	dfs1(root,0,1);
	dfs2(root,root);
	Build(1,1,N);
	while(M--) {
		int opt=read(),x,y,z;
		if(opt==1) {
			x=read();
			y=read();
			z=read();
			z=z%MOD;
			TreeAdd(x,y,z);
		} else if(opt==2) {
			x=read();
			y=read();
			printf("%d\n",TreeSum(x,y));
		} else if(opt==3) {
			x=read(),z=read();
			IntervalAdd(1,idx[x],idx[x]+siz[x]-1,z%MOD);
		} else if(opt==4) {
			x=read();
			printf("%d\n",IntervalSum(1,idx[x],idx[x]+siz[x]-1));
		}
	}
	return 0;
}