Educational DP Contest
A - Frog 1
问题陈述
有\(N\)块石头,编号为\(1, 2, \ldots, N\)。每块\(i\)(\(1 \leq i \leq N\)),石头\(i\)的高度为\(h_i\)。
有一只青蛙,它最初在石块 \(1\) 上。它会重复下面的动作若干次以到达石块\(N\):
- 如果青蛙目前在石块\(i\)上,则跳到石块\(i + 1\)或石块\(i + 2\)上。这里需要付出\(|h_i - h_j|\)的代价,其中\(j\)是要降落的石块。
求青蛙到达石块\(N\)之前可能产生的最小总成本。
简单的线性dp,\(f[i]\)为到达\(i\)的最小的代价,所以转移方程就是\(f[i]=\min( f[i-1] - |h_i-h_{i-1}|,f[i-2]-|h_i-h_{i-2}|)\)
#include<bits/stdc++.h>
using namespace std;
#define int long long
using vi = vector<int>;
using i32 = int32_t;
using pii = pair<int, int>;
using vii = vector<pii>;
const int inf = 1e9, INF = 1e18;
const int mod = 1e9 + 7;
const vi dx = {0, 0, 1, -1}, dy = {1, -1, 0, 0};
i32 main() {
ios::sync_with_stdio(false), cin.tie(nullptr);
int n;
cin >> n;
vi h(n + 1);
for (int i = 1; i <= n; i++) cin >> h[i];
vi f(n + 1);
f[1] = 0, f[2] = abs(h[2] - h[1]);
for (int i = 3; i <= n; i++)
f[i] = min(f[i - 1] + abs(h[i] - h[i - 1]), f[i - 2] + abs(h[i] - h[i - 2]));
cout << f[n] << "\n";
return 0;
}
B - Frog 2
问题陈述
有\(N\)块石头,编号为\(1, 2, \ldots, N\)。每块\(i\)(\(1 \leq i \leq N\)),石头\(i\)的高度为\(h_i\)。
有一只青蛙,它最初在石块 \(1\) 上。它会重复下面的动作若干次以到达石块\(N\):
- 如果青蛙目前在石块\(i\)上,请跳到以下其中一个位置:石块\(i + 1, i + 2, \ldots, i + K\)。这里会产生\(|h_i - h_j|\)的代价,其中\(j\)是要降落的石头。
求青蛙到达石块\(N\)之前可能产生的最小总成本。
与上一题不同的是,这次转移的前驱很多,但依旧可以直接转移,复杂度\(O(NK)\)
#include<bits/stdc++.h>
using namespace std;
#define int long long
using vi = vector<int>;
using i32 = int32_t;
using pii = pair<int, int>;
using vii = vector<pii>;
const int inf = 1e9, INF = 1e18;
const int mod = 1e9 + 7;
const vi dx = {0, 0, 1, -1}, dy = {1, -1, 0, 0};
i32 main() {
ios::sync_with_stdio(false), cin.tie(nullptr);
int n, k;
cin >> n >> k;
vi h(n + 1);
for (int i = 1; i <= n; i++) cin >> h[i];
vi f(n + 1, inf);
f[1] = 0;
for (int i = 2; i <= n; i++)
for (int j = max(1ll, i - k); j < i; j++)
f[i] = min(f[i], f[j] + abs(h[i] - h[j]));
cout << f[n] << "\n";
return 0;
}
C - Vacation
问题陈述
有 \(N\) 天。每\(i\) (\(1 \leq i \leq N\))天,第\(i\)天有三种活动\(A,B,C\),只能进行一种活动,每种活动会获得\(a_i,b_i,c_i\)的快乐值,相邻两天的活动不能相同,请求快乐值之和的最大值。
\(f[i][j]\)表示前\(i\)天,且第\(i\)天进行活动\(j\)的最大快乐值。只需要\(3\times 3\) 的枚举状态和前驱进行转移即可。
#include<bits/stdc++.h>
using namespace std;
#define int long long
using vi = vector<int>;
using i32 = int32_t;
using pii = pair<int, int>;
using vii = vector<pii>;
const int inf = 1e9, INF = 1e18;
const int mod = 1e9 + 7;
const vi dx = {0, 0, 1, -1}, dy = {1, -1, 0, 0};
i32 main() {
ios::sync_with_stdio(false), cin.tie(nullptr);
int n;
cin >> n;
vector<array<int, 3>> v(n), f(n);
for (auto &it: v)
for (auto &i: it) cin >> i;
f[0] = v[0];
for (int i = 1; i < n; i++)
for (int x = 0; x < 3; x++) {
for (int y = 0; y < 3; y++)
if (x != y) f[i][x] = max(f[i][x], f[i - 1][y]);
f[i][x] += v[i][x];
}
cout << ranges::max(f.back()) << "\n";
return 0;
}
D - Knapsack 1
问题陈述
有 \(N\) 个项目,编号为 \(1, 2, \ldots, N\)。对于每个\(i\)(\(1 \leq i \leq N\)),项目\(i\)的权重为\(w_i\),值为\(v_i\)。
太郎决定从\(N\)件物品中选择一些装进背包里带回家。背包的容量为 \(W\),这意味着所取物品的权重之和最多为 \(W\)。
求太郎带回家的物品价值的最大可能和。
01背包
#include <bits/stdc++.h>
using namespace std;
using i32 = int32_t;
using i64 = long long;
using vi = vector<i64>;
int main() {
ios::sync_with_stdio(false), cin.tie(nullptr);
int n, m;
cin >> n >> m;
vi f(m + 1);
for (int w, v; n; n--) {
cin >> w >> v;
for (int i = m; i >= w; i--) f[i] = max(f[i], f[i - w] + v);
}
cout << f.back() << "\n";
return 0;
}
E - Knapsack 2
问题陈述
有 \(N\) 个项目,编号为 \(1, 2, \ldots, N\)。对于每个\(i\)(\(1 \leq i \leq N\)),项目\(i\)的权重为\(w_i\),值为\(v_i\)。
太郎决定从\(N\)件物品中选择一些装进背包里带回家。背包的容量为 \(W\),这意味着所取物品的权重之和最多为 \(W\)。
求太郎带回家的物品价值的最大可能和。
还是 01 背包,但是本题中\(W\)范围非常大,无法枚举。这也用到了一个常用的优化思路,考虑\(N\times v_i\le 10^5\),所以可以背包求出价值为\(i\)的最小代价,然后找到合法的最大值即可。
#include <bits/stdc++.h>
using namespace std;
using i32 = int32_t;
using i64 = long long;
using vi = vector<i64>;
const i64 inf = 1e18;
int main() {
ios::sync_with_stdio(false), cin.tie(nullptr);
int n, m;
cin >> n >> m;
int N = n * 1e3;
vi f(N + 1, inf);
f[0] = 0;
for (int w, v; n; n--) {
cin >> w >> v;
for (int i = N; i >= v; i--) f[i] = min(f[i], f[i - v] + w);
}
for (int i = N; i >= 0; i--)
if (f[i] <= m) {
cout << i << "\n";
return 0;
}
return 0;
}
F - LCS
问题陈述
给你字符串 \(s\) 和 \(t\)。请找出一个最长的字符串,它同时是 \(s\) 和 \(t\) 的子串。
典题求 LCS 并还原。
#include <bits/stdc++.h>
using namespace std;
using i32 = int32_t;
using i64 = long long;
#define int i64
using vi = vector<i64>;
using pii = pair<int, int>;
const i64 inf = 1e18;
i32 main() {
ios::sync_with_stdio(false), cin.tie(nullptr);
string a, b;
cin >> a >> b;
int n = a.size(), m = b.size();
vector f(n + 1, vi(m + 1)), is(n + 1, vi(m + 1));
vector lst(n + 1, vector<pii>(m + 1));
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++) {
if (f[i - 1][j] > f[i][j - 1]) f[i][j] = f[i - 1][j], lst[i][j] = pair(i - 1, j);
else f[i][j] = f[i][j - 1], lst[i][j] = pair(i, j - 1);
if (a[i - 1] == b[j - 1] and f[i - 1][j - 1] + 1 > f[i][j])
is[i][j] = 1, f[i][j] = f[i - 1][j - 1] + 1, lst[i][j] = pair(i - 1, j - 1);
}
string res = "";
for (int i = n, j = m; i and j;) {
if (is[i][j]) res += a[i - 1];
tie(i, j) = lst[i][j];
}
reverse(res.begin(), res.end());
cout << res << "\n";
return 0;
}
G - Longest Path
问题陈述
有一个有向图\(G\),它有\(N\)个顶点和\(M\)条边。顶点编号为 \(1, 2, \ldots, N\),对于每个 \(i\) (\(1 \leq i \leq M\)),\(i\)条有向边从顶点 \(x_i\) 到 \(y_i\)。\(G\)不包含有向循环。
求\(G\)中最长有向路径的长度。这里,有向路径的长度就是其中边的数量。
因为不存在有向环,所以最长的路径起点一定入度为 0终点一定出度为 0。想到这个结论后,比较容易想的就是在拓扑序上线性递推即可。
#include <bits/stdc++.h>
using namespace std;
using i32 = int32_t;
using i64 = long long;
#define int i64
using vi = vector<i64>;
using pii = pair<int, int>;
const i64 inf = 1e18;
i32 main() {
ios::sync_with_stdio(false), cin.tie(nullptr);
int n, m;
cin >> n >> m;
vector<vi> e(n + 1);
vi inDeg(n + 1);
for (int i = 1, x, y; i <= m; i++)
cin >> x >> y, inDeg[y]++, e[x].push_back(y);
queue<int> q;
for (int i = 1; i <= n; i++)
if (inDeg[i] == 0) q.push(i);
vi dis(n + 1);
for (int x; not q.empty();) {
x = q.front(), q.pop();
for (auto y: e[x]) {
dis[y] = max(dis[y], dis[x] + 1);
if (--inDeg[y] == 0) q.push(y);
}
}
cout << ranges::max(dis) << "\n";
return 0;
}
H - Grid 1
问题陈述
有一个网格,横向有 \(H\) 行,纵向有 \(W\) 列。让 \((i, j)\) 表示从上往下第 \(i\) 行和从左往上第 \(j\) 列的正方形。
对于每个\(i\)和\(j\)(\(1 \leq i \leq H\),\(1 \leq j \leq W\)),方格\((i, j)\)由一个字符\(a_{i, j}\)来描述。如果 \(a_{i, j}\) 是
.,则方格 \((i, j)\) 是一个空方格;如果 \(a_{i, j}\) 是#,则方格 \((i, j)\) 是一个墙方格。可以保证方格\((1, 1)\)和\((H, W)\)是空方格。太郎会从方格\((1, 1)\)开始,通过反复向右或向下移动到相邻的空方格,到达\((H, W)\)。
求太郎从\((1, 1)\)到\((H, W)\)的路径数。由于答案可能非常大,请求取\(10^9 + 7\)的模数。
简单的二维转移
#include <bits/stdc++.h>
using namespace std;
using i32 = int32_t;
using i64 = long long;
#define int i64
using vi = vector<i64>;
using pii = pair<int, int>;
const i64 inf = 1e18;
const i64 mod = 1e9 + 7;
i32 main() {
ios::sync_with_stdio(false), cin.tie(nullptr);
int n, m;
cin >> n >> m;
vector<string> g(n);
for (auto &i: g) cin >> i;
vector f(n, vi(m));
f[0][0] = (g[0][0] == '.');
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++) {
if (i == 0 and j == 0) continue;
if (g[i][j] == '#') continue;
if (i > 0) f[i][j] = (f[i][j] + f[i - 1][j]) % mod;
if (j > 0) f[i][j] = (f[i][j] + f[i][j - 1]) % mod;
}
cout << f[n - 1][m - 1] << "\n";
return 0;
}
I - Coins
问题陈述
设 \(N\) 是一个正奇数。
有 \(N\) 枚硬币,编号为 \(1, 2, \ldots, N\)。对于每个 \(i\) (\(1 \leq i \leq N\)),当抛掷硬币 \(i\) 时,正面出现的概率为 \(p_i\),反面出现的概率为 \(1 - p_i\)。
太郎抛出了所有的 \(N\) 枚硬币。求正面比反面多的概率。
简单的概率 dp,设\(f[i][j]\)表示前\(i\)个硬币\(j\)个正面的个数,转移如下:
显然可以通过倒序枚举优化掉一维空间。
答案就是\(\sum (f[n][i] \times( i > n - i ))\)
#include <bits/stdc++.h>
using namespace std;
using i32 = int32_t;
using i64 = long long;
using ldb = long double;
#define int i64
using vi = vector<i64>;
using pii = pair<int, int>;
const i64 inf = 1e18;
const i64 mod = 1e9 + 7;
i32 main() {
ios::sync_with_stdio(false), cin.tie(nullptr);
int n, m;
cin >> n;
vector<ldb> f(n + 1);
f[0] = 1;
for (ldb p, t = n; t > 0; t -= 1) {
cin >> p;
for (int i = f.size() - 1; i >= 0; i--) {
f[i] *= (1.0 - p);
if (i > 0) f[i] += f[i - 1] * p;
}
}
ldb res = 0;
for (int i = 0; i <= n; i++)
res += (i * 2 > n) * f[i];
cout << fixed << setprecision(10) << res << "\n";
return 0;
}
J - Sushi
问题陈述
有\(N\)道菜,编号为\(1, 2, \ldots, N\)。最初,每个\(i\)(\(1 \leq i \leq N\)),\(i\)盘都有\(a_i\)(\(1 \leq a_i \leq 3\))个寿司。(\(1 \leq a_i \leq 3\)) 块寿司。
太郎会重复执行以下操作,直到所有寿司都被吃掉:
- 掷一个骰子,骰子上显示的数字\(1, 2, \ldots, N\)的概率相等,结果为\(i\)。如果骰子\(i\)上有几块寿司,就吃掉其中一块;如果没有,就什么都不吃。
求在所有寿司都被吃掉之前进行该操作的预期次数。
可以注意到的是选择哪个盘子无所谓,答案与盘子的顺序无关,只与盘子中剩下寿司数量有关。
可以设状态为\(f[a][b][c]\)表示当前有\(a\)个盘子剩1 个,\(b\)个盘子剩 2 两个,\(c\)个盘子剩三个的期望操作次数。
则有\(\frac {a} {n}\)的概率选择剩 1 个的盘子,\(\frac {b}{n}\)的概率选到剩 2 个的盘子,\(\frac {c}{n}\)的概率选到剩 3 个的盘子,\(\frac {n-a-b-c}{n}\)的概率选到剩 0 个的盘子。
所以转移方程为
可以看到\(f[a][b][c]\)出现在了方程两侧,所以可以把方程移项得到
根据这个方程便可以进行转移,但枚举比较复杂,所以可以使用深搜加记忆化实现代码
#include <bits/stdc++.h>
using namespace std;
using i32 = int32_t;
using i64 = long long;
using ldb = long double;
#define int long long
using vi = vector<int>;
using pii = pair<int, int>;
const int inf = 1e9;
const int N = 301;
const ldb eps = 1e-6;
ldb f[N][N][N];
int n;
ldb calc(int a, int b, int c) {
if (a == 0 and b == 0 and c == 0) return 0;
if (f[a][b][c] >= eps) return f[a][b][c];
ldb q = a + b + c;
f[a][b][c] = (ldb) n / q;
if (a > 0) f[a][b][c] += (ldb) a / q * calc(a - 1, b, c);
if (b > 0) f[a][b][c] += (ldb) b / q * calc(a + 1, b - 1, c);
if (c > 0) f[a][b][c] += (ldb) c / q * calc(a, b + 1, c - 1);
return f[a][b][c];
}
i32 main() {
ios::sync_with_stdio(false), cin.tie(nullptr);
cin >> n;
int a = 0, b = 0, c = 0;
for (int i = 1, x; i <= n; i++) {
cin >> x;
if (x == 1) a++;
else if (x == 2) b++;
else c++;
}
cout << fixed << setprecision(20)<< calc(a,b,c) << "\n";
return 0;
}
K - Stones
问题陈述
有一个由 \(N\) 个正整数组成的集合 \(A = \{ a_1, a_2, \ldots, a_N \}\)。太郎和二郎将进行下面的对弈。
最初,我们有一堆由 \(K\) 个石子组成的棋子。从太郎开始,两位棋手交替进行以下操作:
- 在\(A\)中选择一个元素\(x\),然后从棋子堆中移走正好\(x\)个棋子。
当棋手无法下棋时,他就输了。假设两位棋手都以最佳状态下棋,请确定获胜者。
如果当前没有石子,则为先手必败态。所有能够一步到达先手必败的状态均为先手必胜态,无论如何都到达不了先手必败态的状态就是先手必败态。
#include <bits/stdc++.h>
using namespace std;
using i32 = int32_t;
using i64 = long long;
using ldb = long double;
#define int long long
using vi = vector<int>;
using pii = pair<int, int>;
i32 main() {
ios::sync_with_stdio(false), cin.tie(nullptr);
int n, k;
cin >> n >> k;
vi a(n);
for (auto &i: a) cin >> i;
vector<bool> f(k + 1);
for (int i = 1; i <= k; i++)
for (auto x: a) {
if (i - x < 0) continue;
if (f[i - x] == 0) {
f[i] = 1;
break;
}
}
if (f.back()) cout << "First\n";
else cout << "Second\n";
return 0;
}
L - Deque
问题陈述
太郎和二郎将进行以下对弈。
最初,他们得到一个序列 \(a = (a_1, a_2, \ldots, a_N)\)。在 \(a\) 变为空之前,两位棋手从太郎开始交替执行以下操作:
- 移除 \(a\) 开头或结尾的元素。棋手获得\(x\)分,其中\(x\)为移除的元素。
假设\(X\)和\(Y\)分别是太郎和二郎在游戏结束时的总得分。太郎试图最大化\(X - Y\),而二郎试图最小化\(X - Y\)。
假设两位棋手的下法都是最优的,请找出\(X - Y\)的结果值。
设\(f[l][r][1]\)表示区间\([l,r]\)中\(X-Y\)的最大值且最后一次操作是太郎,\(f[l][r][0]\)表示区间\([l,r]\)中\(Y-X\)的最大值二郎,所以转移如下:
然后发现两个方程的转移是完全一样的,且最终得到的结果也是一样的,所以可以省略掉第三位。
#include <bits/stdc++.h>
using namespace std;
using i32 = int32_t;
using i64 = long long;
using ldb = long double;
#define int long long
using vi = vector<int>;
using pii = pair<int, int>;
const int inf = 1e18;
i32 main() {
ios::sync_with_stdio(false), cin.tie(nullptr);
int n;
cin >> n;
vi a(n);
for (auto &i: a) cin >> i;
vector f(n, vi(n, -inf));
auto calc = [&](auto &&self, int l, int r) -> i64 {
if (l > r) return 0ll;
if (f[l][r] != -inf) return f[l][r];
f[l][r] = max(a[l] - self(self, l + 1, r), a[r] - self(self, l, r - 1));
return f[l][r];
};
cout << calc(calc, 0, n - 1) << "\n";
return 0;
}
M - Candies
问题陈述
有\(N\)个孩子,编号为\(1, 2, \ldots, N\)。
他们决定分享\(K\)颗糖果。在这里,每个\(i\)(\(1 \leq i \leq N\)),\(i\)个孩子必须分到\(0\)到\(a_i\)颗糖果(包括\(0\)和\(a_i\))。另外,糖果不能剩下。
求他们分享糖果的方法数,模数为 \(10^9 + 7\)。在这里,如果有一个孩子得到的糖果数量不同,那么这两种方法就是不同的。
前缀和优化。
首先\(dp[i][j]\)表示前\(i\)个人共分得\(j\)个糖果的方案数。下一个套路就是枚举第\(i\)个人分到的多少糖果,但是这样做复杂度太高了,转移如下
如果我们维护出了\(dp[i-1][k]\)的前缀和,这就可以省掉一维的枚举。
#include <bits/stdc++.h>
using namespace std;
using i32 = int32_t;
using i64 = long long;
using ldb = long double;
#define int long long
using vi = vector<int>;
using pii = pair<int, int>;
const int mod = 1e9 + 7;
const int inf = 1e18;
i32 main() {
ios::sync_with_stdio(false), cin.tie(nullptr);
int n, k;
cin >> n >> k;
vi a(n + 1);
for (int i = 1; i <= n; i++) cin >> a[i];
vector f(n + 1, vi(k + 1)), sum(n + 1, vi(k + 1));
f[1][0] = sum[1][0] = 1;
for (int i = 1; i <= k; i++)
f[1][i] = i <= a[1], sum[1][i] = sum[1][i - 1] + f[1][i];
for (int i = 2; i <= n; i++) {
f[i][0] = sum[i][0] = 1;
for (int j = 1; j <= k; j++) {
if (j <= a[i]) f[i][j] = sum[i - 1][j];
else f[i][j] = (sum[i - 1][j] - sum[i - 1][j - a[i] - 1] + mod) % mod;
sum[i][j] = (sum[i][j - 1] + f[i][j]) % mod;
}
}
cout << f[n][k] << "\n";
return 0;
}
N - Slimes
问题陈述
有 \(N\) 个黏液排成一排。最初,左边的 \(i\) 个黏液的大小是 \(a_i\) 。
太郎正试图将所有的黏液组合成一个更大的黏液。他会反复执行下面的操作,直到只有一个粘液为止:
- 选择两个相邻的粘液,将它们组合成一个新的粘液。新黏液的大小为 \(x + y\) ,其中 \(x\) 和 \(y\) 是合并前黏液的大小。这里需要花费 \(x + y\) 。在组合粘泥时,粘泥的位置关系不会改变。
求可能产生的最小总成本。
区间dp模板。
\(f[l][r]\)表示区间把\([l,r]\)合并的最小代价。
我们枚举出\([l,r]\)然后枚举出分界点\(mid\),然后可以转移
所以我们枚举区间的时候必须要从小到大。
#include <bits/stdc++.h>
using namespace std;
using i32 = int32_t;
using i64 = long long;
using ldb = long double;
#define int i64
using vi = vector<int>;
using pii = pair<int, int>;
const int inf = 1e18;
const int mod = 1e9 + 7;
const vi dx = {0, 0, 1, -1}, dy = {1, -1, 0, 0};
i32 main() {
ios::sync_with_stdio(false), cin.tie(nullptr);
int n;
cin >> n;
vi a(n + 1);
for (int i = 1; i <= n; i++)
cin >> a[i], a[i] += a[i - 1];
vector f(n + 1, vi(n + 1, inf));
for (int i = 1; i <= n; i++) f[i][i] = 0;
for (int len = 2; len <= n; len++)
for (int l = 1, r = len; r <= n; l++, r++)
for (int mid = l; mid + 1 <= r; mid++)
f[l][r] = min(f[l][r], f[l][mid] + f[mid + 1][r] + a[r] - a[l - 1]);
cout << f[1][n] << "\n";
return 0;
}
O - Matching
问题陈述
有 \(N\) 名男性和 \(N\) 名女性,编号均为 \(1, 2, \ldots, N\) 。
对于每个 \(i, j\) ( \(1 \leq i, j \leq N\) ),男人 \(i\) 和女人 \(j\) 的相容性都是一个整数 \(a _{i, j}\) 。如果是 \(a_{i, j} = 1\) ,则男人 \(i\) 和女人 \(j\) 相容;如果是 \(a _ {i, j} = 0\) ,则不相容。
太郎试图做出 \(N\) 对,每对都由一个相容的男人和一个相容的女人组成。在这里,每个男人和每个女人必须正好属于一对。
求太郎能凑成 \(N\) 对的方式数,模为 \(10^9 + 7\) 。
简单的状压 dp,设状态为\(f[i][t]\)表示前\(i\)个男生,匹配女生状态\(t\)的方案数,其中\(t\)是一个二进制数每一位 01 表示一位女生是否完成匹配。每次只要枚举状态,然后再枚举当前男生和哪一位女生匹配即可计算出前驱状态。
#include <bits/stdc++.h>
using namespace std;
using i32 = int32_t;
using i64 = int64_t;
using vi = vector<i64>;
using pii = pair<i64, i64>;
const i64 mod = 1e9 + 7;
i32 main() {
ios::sync_with_stdio(false), cin.tie(nullptr);
int n;
cin >> n;
vector a(n, vi(n));
for (auto &ai: a)
for (auto &aij: ai) cin >> aij;
int N = 1 << n;
vector f(n+1, vi(N));
f[0][0] = 1;
for (int i = 1; i <= n; i++) {
for (int t = 0; t < N; t++) {
if (i != __builtin_popcount(t)) continue;
for (int j = 0; j < n; j++) {
if ((1 << j) & t == 0 or a[i - 1][j] == 0) continue;
f[i][t] = (f[i][t] + f[i - 1][t ^ (1 << j)]) % mod;
}
}
}
cout << f[n][N - 1] << "\n";
return 0;
}
P - Independent Set
问题陈述
有一棵树,树上有 \(N\) 个顶点,编号为 \(1, 2, \ldots, N\) 。对于每个 \(i\) ( \(1 \leq i \leq N - 1\) ), \(i\) -th 边连接顶点 \(x_i\) 和 \(y_i\) 。
太郎决定将每个顶点涂成白色或黑色。这里不允许将相邻的两个顶点都涂成黑色。
求 \(10^9 + 7\) 模中可以涂抹顶点的方法的个数。
树形 dp,\(f[i][0/1]\)表示\(i\)好的白或黑的方案数,然后我们可以枚举子节点,要知道白色的子节点黑白任意,黑色的子节点只有黑色。
#include <bits/stdc++.h>
using namespace std;
using i32 = int32_t;
using i64 = int64_t;
#define int i64
using vi = vector<i64>;
using pii = pair<i64, i64>;
const i64 mod = 1e9 + 7;
vector<vi> e;
vector<array<int, 2>> f;
void dfs(int x, int fa) {
f[x][0] = f[x][1] = 1;
for (auto y: e[x]) {
if (y == fa) continue;
dfs(y, x);
f[x][1] = f[x][1] * f[y][0] % mod;
f[x][0] = f[x][0] * (f[y][0] + f[y][1]) % mod;
}
return;
}
i32 main() {
ios::sync_with_stdio(false), cin.tie(nullptr);
int n;
cin >> n;
e.resize(n + 1), f.resize(n + 1);
for (int i = 1, x, y; i < n; i++) {
cin >> x >> y;
e[x].push_back(y);
e[y].push_back(x);
}
dfs(1, -1);
cout << (f[1][0] + f[1][1]) % mod;
return 0;
}
Q - Flowers
问题陈述
有 \(N\) 朵花排成一排。对于每一朵 \(i\) ( \(1 \leq i \leq N\) ),从左边起第 \(i\) 朵花的高和美分别是 \(h_i\) 和 \(a_i\) 。这里, \(h_1, h_2, \ldots, h_N\) 都是不同的。
太郎正在拔掉一些花朵,以便满足以下条件:
- 剩余花朵的高度从左到右单调递增。
求剩余花朵的美之和的最大值。
发现高度的值域其实很小,所以可以设状态为\(f[i][j]\)表示前\(i\)朵花,且最大高度不超过\(j\)的美之和最大值。则有转移如下
然后很容易就可以压缩掉一维,然后转移就变成求前缀最大值。求前缀最大值可以用树状数组实现。
#include <bits/stdc++.h>
using namespace std;
using i32 = int32_t;
using i64 = int64_t;
#define int i64
using vi = vector<i64>;
using pii = pair<i64, i64>;
const i64 mod = 1e9 + 7;
const i64 inf = 1e18;
struct BinaryIndexedTree {
#define lowbit(x) ( x & -x )
int n;
vector<int> b;
BinaryIndexedTree(int n) : n(n), b(n + 1, 0) {};
void update(int i, int y) {
for (; i <= n; i += lowbit(i)) b[i] = max(b[i], y);
return;
}
int calc(int i) {
int ans = 0;
for (; i; i -= lowbit(i)) ans = max(ans, b[i]);
return ans;
}
};
i32 main() {
ios::sync_with_stdio(false), cin.tie(nullptr);
int n;
cin >> n;
vi h(n), a(n);
for (int &i: h) cin >> i;
for (int &i: a) cin >> i;
int ans = 0;
BinaryIndexedTree bit(n);
for (int i = 0, tmp; i < n; i++) {
tmp = bit.calc(h[i] - 1) + a[i];
ans = max(ans, tmp);
bit.update(h[i], tmp);
}
cout << ans << "\n";
return 0;
}
R - Walk
问题陈述
有一个简单的有向图 \(G\) ,其顶点为 \(N\) ,编号为 \(1, 2, \ldots, N\) 。
对于每个 \(i\) 和 \(j\) ( \(1 \leq i, j \leq N\) ),你都会得到一个整数 \(a_{i, j}\) ,表示顶点 \(i\) 到 \(j\) 之间是否有一条有向边。如果是 \(a_{i, j} = 1\) ,则存在一条从顶点 \(i\) 到 \(j\) 的有向边,如果是 \(a_{i, j} = 0\) ,则没有。
求在 \(G\) 中长度为 \(K\) 的不同有向路径的数目,模数为 \(10^9 + 7\) 。我们还将计算多次穿越同一条边的路径。
我们设\(f_i[x][y]\)表示长度为\(i\)且从\(x\)到\(y\)的路径的方案数,则输入的矩阵就是\(f_1\)。然后我们根据传递闭包得到转移如下
很容易发现这个转移过程就是矩阵乘法
所以可以用矩阵快速幂来解决这个问题。
#include <bits/stdc++.h>
using namespace std;
using i32 = int32_t;
using i64 = int64_t;
#define int i64
using vi = vector<i64>;
using pii = pair<i64, i64>;
const i64 mod = 1e9 + 7;
const i64 inf = 1e18;
struct matrix {
static constexpr int mod = 1e9 + 7;
int x, y;
vector<vector<int>> v;
matrix() {}
matrix(int x, int y) : x(x), y(y) {
v = vector<vector<int>>(x + 1, vector<int>(y + 1, 0));
}
void I() {// 单位化
y = x;
v = vector<vector<int>>(x + 1, vector<int>(x + 1, 0));
for (int i = 1; i <= x; i++) v[i][i] = 1;
return;
}
void display() { // 打印
for (int i = 1; i <= x; i++)
for (int j = 1; j <= y; j++)
cout << v[i][j] << " \n"[j == y];
return;
}
friend matrix operator*(const matrix &a, const matrix &b) { //乘法
assert(a.y == b.x);
matrix ans(a.x, b.y);
for (int i = 1; i <= a.x; i++)
for (int j = 1; j <= b.y; j++)
for (int k = 1; k <= a.y; k++)
ans.v[i][j] = (ans.v[i][j] + a.v[i][k] * b.v[k][j]) % mod;
return ans;
}
friend matrix operator^(matrix x, int y) { // 快速幂
assert(x.x == x.y);
matrix ans(x.x, x.y);
ans.I();//注意一定要先单位化
while (y) {
if (y & 1) ans = ans * x;
x = x * x, y >>= 1;
}
return ans;
}
};
i32 main() {
ios::sync_with_stdio(false), cin.tie(nullptr);
int n, k;
cin >> n >> k;
matrix f(n, n);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
cin >> f.v[i][j];
f = f ^ k;
int res = 0;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
res = (res + f.v[i][j]) % mod;
cout << res << "\n";
return 0;
}
S - Digit Sum
问题陈述
求在 \(1\) 和 \(K\) (含)之间满足以下条件的整数个数,模为 \(10^9 + 7\) :
- 十进制数位之和是 \(D\) 的倍数。
\(f[pos][x]\)表示前\(pos\)位和模\(d\)为\(x\)的数的个数。
然后我们设\(dp(pos,x,flag)\),其中\(flag\)表示前\(pos\)是否完全与原数相同。如果相同则当前位的取值是\([0,a[pos]]\)否则是\([0,9]\)。然后枚举当前位更新状态即可。
注意如果前\(pos\)位不与原数完全相同是,要用记忆化。
#include <bits/stdc++.h>
using namespace std;
using i32 = int32_t;
using i64 = int64_t;
using vi = vector<i64>;
#define int i64
const int mod = 1e9 + 7;
int d;
vi a(1);
vector<vi> f;
int dp(int pos, int x, bool flag) {
if (pos == 0) return x % d == 0;
if (flag and f[pos][x] != -1) return f[pos][x];
int ans = 0, n = flag ? 9 : a[pos];
for (int i = 0; i <= n; i++)
ans = (ans + dp(pos - 1, (x+ i) % d, flag or i < n)) % mod;
if (flag) f[pos][x] = ans;
return ans;
}
i32 main() {
ios::sync_with_stdio(false), cin.tie(nullptr);
string k;
cin >> k >> d;
reverse(k.begin(), k.end());
for (auto i: k) a.push_back(i - '0');
f = vector(a.size(), vi(d, -1));
cout << (dp(a.size() - 1, 0, false) + mod - 1) % mod;
return 0;
}
T - Permutation
问题陈述
设 \(N\) 是一个正整数。给你一个长度为 \(N - 1\) 的字符串 \(s\) ,由
<和>组成。求满足以下条件的 \((1, 2, \ldots, N)\) 的 \((p_1, p_2, \ldots, p_N)\) 排列的个数,模数为 \(10^9 + 7\) :
- 对于每个 \(i\) ( \(1 \leq i \leq N - 1\) ),如果 \(s\) 中的 \(i\) -th 字符是
<,则为 \(p_i \lt p_{i + 1}\) ;如果 \(s\) 中的 \(i\) -th 字符是>,则为 \(p_i \gt p_{i + 1}\) 。
设状态为\(f[i][j]\)表示\([1,i]\)的排列,且最后一位是\(j\)的方案数。
如果符号是\(<\),则\(f[i][j] = \sum_{t = 1} ^{j-1} f[i-1][t]\)
如果符号是\(>\),则\(f[i][j] = \sum_{t=j}^{i} f[i-1][t]\)
这样如果维护了一个前最后就可以\(O(1)\)的进行转移了。
#include <bits/stdc++.h>
using namespace std;
using i32 = int32_t;
using i64 = int64_t;
using vi = vector<i64>;
#define int i64
const int mod = 1e9 + 7;
i32 main() {
ios::sync_with_stdio(false), cin.tie(nullptr);
int n;
string s;
cin >> n >> s;
s = " " + s;
vi sum(n + 1, 1), f(n + 1);
sum[0] = 0;
for (int i = 2; i <= n; i++) {
fill(f.begin(), f.end(), 0);
for (int j = 1; j <= i; j++) {
if (s[i] == '<') f[j] = sum[j - 1];
else f[j] = (sum[i - 1] - sum[j-1] + mod) % mod;
}
for (int j = 1; j <= n; j++)
sum[j] = (sum[j - 1] + f[j]) % mod;
}
int res = 0;
for (int i = 1; i <= n; i++)
res = (res + f[i]) % mod;
cout << res << "\n";
return 0;
}
U - Grouping
问题陈述
有 \(N\) 只兔子,编号为 \(1, 2, \ldots, N\) 。
对于每只 \(i, j\) ( \(1 \leq i, j \leq N\) ),兔子 \(i\) 和 \(j\) 的兼容性用整数 \(a_{i, j}\) 来描述。这里, \(a_{i, i} = 0\) 表示每个 \(i\) ( \(1 \leq i \leq N\) ), \(a_{i, j} = a_{j, i}\) 表示每个 \(i\) 和 \(j\) ( \(1 \leq i, j \leq N\) )。
太郎要把 \(N\) 只兔子分成若干组。在这里,每只兔子必须正好属于一组。分组后,对于每只 \(i\) 和 \(j\) ( \(1 \leq i \lt j \leq N\) ),如果兔子 \(i\) 和 \(j\) 属于同一组,太郎就能获得 \(a_{i, j}\) 分。
求太郎可能得到的最高总分。
设\(f[s]\)表示当前选择选择的兔子集合为\(s\)的最高总分,获得总分只有两种情况,一种是\(s\)所有的兔子在一组中。还有一种是\(s\)由至少两个组拼起来的。
对于只有一组的情况,直接统计一下就好,对于多个组拼起来的则使用枚举的子集的方式来求。
#include<bits/stdc++.h>
using namespace std;
using i32 = int32_t;
using i64 = long long;
#define int i64
using vi = vector<int>;
i32 main() {
ios::sync_with_stdio(false), cin.tie(nullptr);
int n;
cin >> n;
vector a(n, vi(n));
for (auto &ai: a)
for (auto &aij: ai)
cin >> aij;
const int N = 1 << n;
vi f(N);
for (int s = 1; s < N; s++) {
for (int i = 0; i < n; i++) {
if ((s & 1 << i) == 0) continue;
for (int j = 0; j < i; j++) {
if ((s & 1 << j) == 0) continue;
f[s] += a[i][j];
}
}
for (int i = s; i; i = (i - 1) & s)
f[s] = max(f[s], f[i] + f[s ^ i]);
}
cout << f.back() << "\n";
return 0;
}
V - Subtree
问题陈述
给一棵树,对每一个节点染成黑色或白色。
对于每一个节点,求强制把这个节点染成黑色的情况下,所有的黑色节点组成一个联通块的染色方案数,答案对 \(M\) 取模。
换根 dp。
首先可以任意选择一个点做根节点,我代码里面选择的是\(1\),选定根节点后,树就变成了一颗有根树。
现在对于每个点\(x\),如果知道了子树中的合法方案数\(f1[x]\)和非子树节点的合法方案数\(f2[x]\),则答案就是\(f1[x] \times f2[x]\)
考虑求\(f1[x]\),我们可以枚举\(x\)的子节点\(y\),则有如下转移
然后考虑如何求\(f2[x]\),我们已知了\(x\)的父亲节点\(fa\)和兄弟节点\(y\),则有如下转移
其中如果要求解\(\Pi(f1[y]+1)\)的话复杂度是\(O(N^2)\)的,这里因为要取模,所以采用了前缀积和后缀积的方法,\(pre[y]\)表示\(y\)前面兄弟结点的前缀积,\(suf[y]\)表示\(y\)后面兄弟节点的后缀积,则\(f2[x] = f2[fa]\times pre[x]\times suf[x] + 1\)
#include<bits/stdc++.h>
using namespace std;
using i32 = int32_t;
using i64 = long long;
#define int i64
using vi = vector<int>;
int n, mod;
vector<vi> e;
vi f1, f2;
void dp1(int x, int fa) {
f1[x] = 1;
for (auto y: e[x]) {
if (y == fa) continue;
dp1(y, x);
f1[x] = (f1[x] * (f1[y] + 1)) % mod;
}
return;
}
void dp2(int x, int fa) {
if (e[x].empty())return;
vi pre(e[x].size()), suf(e[x].size());
pre.front() = suf.back() = 1;
for (int i = 1; i < e[x].size(); i++) {
if (e[x][i - 1] == fa) pre[i] = pre[i - 1];
else pre[i] = (pre[i - 1] * (f1[e[x][i - 1]] + 1)) % mod;
}
for (int i = e[x].size() - 2; i >= 0; i--) {
if (e[x][i + 1] == fa) suf[i] = suf[i + 1];
else suf[i] = (suf[i + 1] * (f1[e[x][i + 1]] + 1)) % mod;
}
for (int i = 0; i < e[x].size(); i++) {
if (e[x][i] == fa) continue;
f2[e[x][i]] = (f2[x] * pre[i] % mod * suf[i] % mod + 1) % mod;
dp2(e[x][i], x);
}
return;
}
i32 main() {
ios::sync_with_stdio(false), cin.tie(nullptr);
cin >> n >> mod;
e.resize(n + 1), f1.resize(n + 1), f2.resize(n + 1);
for (int x, y, i = 1; i < n; i++)
cin >> x >> y, e[x].push_back(y), e[y].push_back(x);
dp1(1, -1);
f2[1] = 1, dp2(1, -1);
for (int i = 1; i <= n; i++)
cout << f1[i] * f2[i] % mod << "\n";
return 0;
}
W - Intervals
问题陈述
给定 \(m\) 条规则形如 \((l_i,r_i,a_i)\),对于一个 01 串,其分数的定义是:对于第 \(i\) 条规则,若该串在 \([l_i,r_i]\) 中至少有一个 1,则该串的分数增加 \(a_i\)。
你需要求出长度为 \(n\) 的 01 串中的最大分数。
\(1\le n,m\le 2\times 10^5\),\(|a_i|\le 10^9\)。
线段树优化 dp。
设\(f[i][j]\)表示前\(i\)个位置,且最后一个\(1\)的位置为\(j\)的最大分数。并且我们强制规定,对于\((l_k,r_k,a_k)\)我们只考虑\(r_k\le i\)的贡献。显然这里有一个合法条件一定是\(j\le i\),所以有如下的转移
为什么有这样的转移呢?首先如果\(j<i\)则前\(i-1\)位的最后一个也一定是\(j\),如果$j = i $则前面的最后一位是可以任意取的。
然后我们发现对于第一维只和上一位有关,所以可以优化掉一维空间。
然后我们发现转移可以分为两部分。
第一部分是\(f[i] = \max( f[j] )\)。
第二部分是对于所有满足\(r_k=i\)的\((l_k,r_k,a_k)\),都有$ f[j] = f[j] + a_k , (l_k\le j \le r_k)$。
对于这两部分操作,实际上就是区间最值查询和区间修改,可以使用线段树来实现。
#include<bits/stdc++.h>
using namespace std;
using i32 = int32_t;
using i64 = long long;
#define int i64
using vi = vector<int>;
struct Node {
int l, r, val, tag;
Node *left, *right;
Node(int l, int r, int val, int tag, Node *left, Node *right)
: l(l), r(r), val(val), tag(tag), left(left), right(right) {};
} *root;
Node *build(int l, int r) {
if (l == r) return new Node(l, r, 0, 0, nullptr, nullptr);
int mid = (l + r) / 2;
Node *left = build(l, mid), *right = build(mid + 1, r);
return new Node(l, r, 0, 0, left, right);
}
void mark(int v, Node *cur) {
if (cur == nullptr) return;
cur->val += v, cur->tag += v;
return;
}
void pushdown(Node *cur) {
if (cur->tag == 0) return;
mark(cur->tag, cur->left), mark(cur->tag, cur->right);
cur->tag = 0;
return;
}
void modify(int l, int r, int v, Node *cur) {
if (l > cur->r or r < cur->l) return;
if (l <= cur->l and cur->r <= r) {
mark(v, cur);
return;
}
pushdown(cur);
int mid = (cur->l + cur->r) / 2;
if (l <= mid) modify(l, r, v, cur->left);
if (r > mid) modify(l, r, v, cur->right);
cur->val = max(cur->left->val, cur->right->val);
}
i32 main() {
ios::sync_with_stdio(false), cin.tie(nullptr);
int n, m;
cin >> n >> m;
vector<array<int, 3>> a(m);
for (auto &[l, r, v]: a)
cin >> l >> r >> v;
sort(a.begin(), a.end(), [&](const auto &x, const auto &y) {
return x[1] < y[1];
});
root = build(1, n);
for (int i = 1, p = 0; i <= n; i++) {
modify(i, i, root->val, root);
for (; p < m and a[p][1] == i; p++)
modify(a[p][0], i, a[p][2], root);
}
cout << max(0ll, root->val);
return 0;
}
X - Tower
问题陈述
有 \(N\) 块,编号为 \(1, 2, \ldots, N\) 。对于每个 \(i\) ( \(1 \leq i \leq N\) ),积木块 \(i\) 的重量为 \(w_i\) ,坚固度为 \(s_i\) ,价值为 \(v_i\) 。
太郎决定从 \(N\) 块中选择一些,按照一定的顺序垂直堆叠起来,建造一座塔。在这里,塔必须满足以下条件:
- 对于塔中的每个积木块 \(i\) ,堆叠在其上方的积木块的权重之和不大于 \(s_i\) 。
求塔中所包含的图块的最大可能权重之和。
这道题算是贪心优化 dp。
首先考虑什么样的更适合放在下面?如果\(i\)比\(j\)更适合放在下面,则\(s_i-w_k> s_j-w_i\)也就可以化简得到\(s_i+w_i > s_j + w_j\)。这样可以进行一个排序,从小到大排序。
然后我们考虑从上往下放\(f[i]\)表示当前累计重量为\(i\)的最大价值。现在如果枚举到了物品\(j\)则有如下转移
其中\(j\le s_i\),这样就可以转化成经典的 01 背包问题,记得使用倒序枚举。
#include<bits/stdc++.h>
using namespace std;
using i32 = int32_t;
using i64 = long long;
#define int i64
using vi = vector<int>;
const int N = 2e4;
i32 main() {
ios::sync_with_stdio(false), cin.tie(nullptr);
int n;
cin >> n;
vector<array<int, 3>> a(n);
for (auto &[w, s, v]: a) cin >> w >> s >> v;
sort(a.begin(), a.end(), [&](const auto x, const auto &y) {
return x[0] + x[1] < y[0] + y[1];
});
vi f(N + 1);
for (const auto &[w, s, v]: a)
for (int i = s; i >= 0; i--)
f[i + w] = max(f[i + w], f[i] + v);
cout << ranges::max(f);
return 0;
}
Y - Grid 2
问题陈述
给一个 \(H\times W\) 的网格,每一步只能向右或向下走,给出 \(N\) 个坐标 \((r_1,c_1),(r_2,c_2),...,(r_n,c_n)\),这些坐标对应的位置不能经过,求从左上角 \((1,1)\) 走到右下角 \((H,W)\) 的方案数,答案对 \(10^9+7\) 取模。
\(2 \leq H, W \leq 10^5 ,1 \leq N \leq 3000\)
首先从一个点到\((x_1,y_1)\)到\((x_2,y_2)\)的路径数有\(C(x_1 + y_1 - x_2 - y_2 , x_1 - x_2)\)中。
记从\((1,1)\)到\((x_i,y_i)\)不经过任何障碍物的路径数\(f[i]\),则有如下转移
其中\(j\)是比\(i\)更靠近起点的点。看起来是容斥掉了一个点,让实际上因为我们记录的是不经过任何障碍物的路径,所以容斥的时候是不会重复容斥的。
#include<bits/stdc++.h>
using namespace std;
using i32 = int32_t;
using i64 = long long;
#define int i64
using vi = vector<int>;
using pii = pair<int, int>;
const int mod = 1e9 + 7;
const int N = 2e5;
int power(int x, int y) {
int ans = 1;
while (y) {
if (y & 1) ans = ans * x % mod;
x = x * x % mod, y /= 2;
}
return ans;
}
int inv(int x) {
return power(x, mod - 2);
}
vi fact, invFact;
int C(int x, int y) {
return fact[x] * invFact[x - y] % mod * invFact[y] % mod;
}
void init() {
fact.resize(N + 1), invFact.resize(N + 1);
fact[0] = 1, invFact[0] = inv(1);
for (int i = 1; i <= N; i++)
fact[i] = fact[i - 1] * i % mod, invFact[i] = inv(fact[i]);
return;
}
i32 main() {
ios::sync_with_stdio(false), cin.tie(nullptr);
init();
int h, w, n;
cin >> h >> w >> n;
vector<pii> a(n);
for (auto &[x, y]: a) cin >> x >> y;
sort(a.begin(), a.end(), [&](const auto &x, const auto &y) {
return x.first + x.second < y.first + y.second;
});
a.emplace_back(h, w);
vi f(n + 1);
for (int i = 0; i <= n; i++)
f[i] = C(a[i].first + a[i].second - 2, a[i].first - 1);
for (int i = 0; i <= n; i++) {
auto &[xi, yi] = a[i];
for (int j = 0; j <= n; j++) {
auto &[xj, yj] = a[j];
if (i == j or xi < xj or yi < yj) continue;
f[i] = (f[i] - f[j] * C(xi + yi - xj - yj, xi - xj) % mod + mod) % mod;
}
}
cout << f[n] << "\n";
return 0;
}
Z - Frog 3
问题陈述
有 \(N\) 块石头,编号为 \(1, 2, \ldots, N\) 。每块 \(i\) ( \(1 \leq i \leq N\) )石头 \(1 \leq i \leq N\) ),石头 \(i\) 的高度为 \(h_i\) 。这里, \(h_1 \lt h_2 \lt \cdots \lt h_N\) 成立。
有一只青蛙,它最初位于石块 \(1\) 上。它会重复下面的动作若干次以到达石块 \(N\) :
- 如果青蛙目前在 \(i\) 号石块上,请跳到以下其中一块:石块 \(i + 1, i + 2, \ldots, N\) 。这里需要花费 \((h_j - h_i)^2 + C\) ,其中 \(j\) 是要落脚的石头。
求青蛙到达石块 \(N\) 之前可能产生的最小总成本。
\(2 \leq N \leq 2 \times 10^5\)
斜率优化 dp。
设\(f[i]\)表示从\(1\)到\(i\)的最小花费,这可以写出最基础的状态转移为
内部可以展开为
把无关项提出来,可以得到
令\(g_i = f_i + h_i^2\),则有
至此,关于式子的化简就结束了,现在对于转移,如果有两个点\(x,y\),若满足\(x<y\)且\(x\)更优,则有
移项得
发现这个式子和斜率很像,所以令\(slop(x,y)=\frac{g_x-g_y}{h_x - h_y}\)。
下面就开始时斜率优化的部分,有三个点\(1<2<3\),如果\(2\)是最优的则有
对于下图
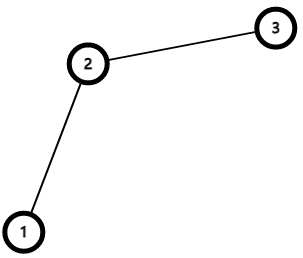
发现\(slop(1,2)>slop(2,3)\),因此\(2\)一定不是最优的,所以可以优化成
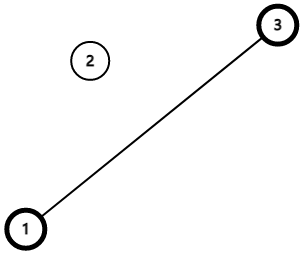
最后你会发现,实际上就是维护一个凸包
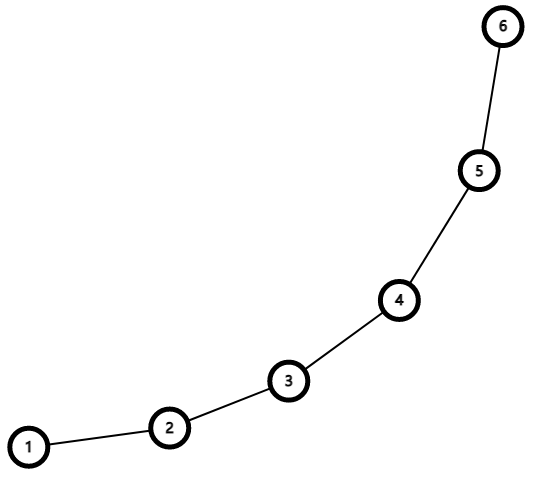
然后,因为本题的\(h_i\)时保证递增的,所以最优解只会出现在队首
#include<bits/stdc++.h>
using namespace std;
using i32 = int32_t;
using i64 = long long;
using ldb = long double;
#define int i64
using vi = vector<int>;
using pii = pair<int, int>;
i32 main() {
ios::sync_with_stdio(false), cin.tie(nullptr);
int n, C;
cin >> n >> C;
vi h(n + 1), f(n + 1), g(n + 1);
for (int i = 1; i <= n; i++) cin >> h[i];
auto slop = [&](int x, int y) {
return ldb(g[x] - g[y]) / ldb(h[x] - h[y]);
};
deque<int> q;
q.push_back(1), g[1] = h[1] * h[1];
for (int i = 2, j; i <= n; i++) {
while (q.size() >= 2 and slop(q.front(), *(q.begin() + 1)) <= 2 * h[i]) q.pop_front();
j = q.front();
f[i] = h[i] * h[i] + C + g[j] - 2 * h[i] * h[j];
g[i] = f[i] + h[i] * h[i];
while (q.size() >= 2 and slop(*(q.rbegin() + 1), q.back()) >= slop(q.back(), i)) q.pop_back();
q.push_back(i);
}
cout << f[n];
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号