OI时期写的luogu部分题解

luogu P3378 【模板】堆

如题，初始小根堆为空，我们需要支持以下3种操作：

操作1： 1 x 表示将x插入到堆中

操作2： 2 输出该小根堆内的最小数

操作3： 3 删除该小根堆内的最小数

#include<bits/stdc++.h>
using namespace std;


const int N = 1e6+5;
int n,i,t,x,tot = 0,now,nxt;
int v[N];


inline int read()
{
	int x = 0;
	char ch =getchar();
	while(ch < '0' || ch > '9') ch = getchar();
	while(ch >='0' && ch <= '9')
	{
		x = x*10 + ch-'0';
		ch = getchar();
	}
	return x;
}

inline void insert()
{
	x = read();
	v[++tot] = x;
	now = tot;
	while(v[now>>1] > v[now]) 
	{
		swap(v[now>>1] , v[now]);
		now = now>>1;
	}
}

inline void del()
{
	v[1] = v[tot--];
	now = 1;
	while((now<<1) <= tot)
	{
		nxt = now<<1;
		if(nxt+1 <= tot && v[nxt+1] < v[nxt]) nxt++;
		if(v[nxt] < v[now]) swap(v[now],v[nxt]);
		else break;
		now = nxt; 
	}
}

int main()
{
	n = read();
	for(i = 1;i <= n;i++)
	{
		t = read();
		if(t == 1) insert();
		if(t == 2) printf("%d\n",v[1]);
		if(t == 3) del();
	}
	return 0;
}

luogu P1037 【产生数】

貌似都是用佛洛依德写的，我就来个\(DFS\)搜索的方法吧。

首先通过字符串读入来读入这个数字。

然后对每一位数字进行\(DFS\)，每搜索到一个数字计数器加一。最后根据分步计算原理，将每位数可扩展的数进行相乘输出即可。

另外第四、第五组数据较大好久没有写高精度写挂了好几次。

#include<bits/stdc++.h>
using namespace std;


string num;
int k,a[20],b[20],ans = 0,sum[30] = {};//ans每一位可以扩展多少个数字
bool vis[10] = {};//vis记录当前数字有没有被搜过


inline int read()//快读
{
	int x = 0;
	char ch = getchar();
	while(ch < '0' || ch > '9') ch = getchar();
	while(ch >= '0' && ch <= '9')
	{
		x = (x<<3)+(x<<1) + ch-'0';
		ch = getchar();
	}
	return x;
}

inline void mul(int a[],int b)//低精度乘高精度
{
	for(int i = 1;i <= a[0];i++)
	{
		a[i] *= b;
	}
	for(int i = 1;i <= a[0];i++)
	{
		if(a[i] >= 10)
		{
			a[i+1] += a[i]/10;
			a[i] %= 10;
			if(i == a[0]) a[0]++;
		}
	}
}

inline void dfs(int x)
{
	vis[x] = 1;//每搜到一个打个标记
	ans++;
	for(int i = 1;i <= k;i++)
	{
		if(a[i] == x && !vis[b[i]])	dfs(b[i]);//如果符合且未被搜索
	}
}


int main()
{
	cin >> num;
	k = read();
	sum[0] = 1;
	sum[1] = 1;
	for(int i = 1;i <= k;i++)
	{
		a[i] = read();
		b[i] = read();
	}
	for(int i = 0;i < num.size();i++)
	{
		dfs(num[i]-'0');
		mul(sum,ans);
		memset(vis,0,sizeof(vis));//消除影响
		ans = 0;
	}
	for(int i = sum[0];i >= 1;i--) printf("%d",sum[i]);
	putchar('\n');

	return 0;
}

题解 P1313 【计算系数】

这道题是一道非常裸地二项式定理

结果很明显就是

\[C^{min(n,m)}_{k} \times a^{m} \times b^{n} \]

首先\(a^{m}\)和\(b^{n}\)用快速幂计算不多说

但我们\(C^{min(n,m)}_{k}\)比较难搞

先看组合数的公式

\[C^{m}_{n} = \frac{n!}{m!(n-m)!} = \frac{n(n-1)(n-2) \cdots (n-m+1)}{1\times2\times3\times\cdots\times m} \]

看到这个式子很明显以为要取模所以我们不能直接用除法，要变成乘分母的逆元

但是我不会逆元这该怎么办办呢？

首先在高中数学里是没有逆元的，我们也不需要取模。所以我们在计算组合数的时候就是先去约分。在这里分母上的一个数最大是1000不用取模。所以我们可以先枚举分母上的每一个数字，再枚举分子上的一个数字进行约分，约这两个数的\(GCD\)。因为是组合数，所以最后我们一定可以约分成分母是\(1\)的情况这个是候在根据随时取模原理做乘法就好

这样就可以避免使用逆元

#include <bits/stdc++.h>
#define LL long long
using namespace std;


const int N = 1e6+5;
const LL mod = 10007;
LL a,b,k,n,m,result = 1,t[N];


inline LL gcd(LL a,LL b) {return !b?a:gcd(b,a%b);}

inline LL ksm(LL a,LL b)
{
    register LL ans = 1;
    while(b)
    {
        if(b & 1) ans = (ans * a) % mod;
        a = (a * a) % mod;
        b >>= 1;
    }
    return ans % mod;
}


int main()
{
    cin >> b >> a >> k >> n >> m;
        
    result = (result * ksm(b,n)) % mod;
    result = (result * ksm(a,m)) % mod;
    
    n = min(n,m);
    
    for(register int i = 1,j = k - n + 1;i <= n;i ++,j ++) t[i] = j;
    
    for(register int i = 2;i <= n;i ++)
    {
        register LL x = i,y;
        for(register int j = 1;j <= n;j ++)
        {
            if(x > t[j]) y = gcd(x,t[j]);
            else y = gcd(t[j],x);
            if(y == 1) continue;
            x /= y; t[j] /= y;
            if(x == 1) break;
        }
    }
    
    for(register int i = 1;i <= n;i ++) result = (result * t[i]) % mod;
    
    cout << result << endl;
}

luogu P1199 【三国游戏】

首先很明显这是一道贪心题。

贪心方法很多dalao已经写出来了，找每个武将次大值最大的武将。

呢么我们定义一个数组\(f[N][2]\) ， 其中\(f[i][0]\)用来储存第\(i\)个武将的次大值、\(f[i][1]\)来存储第\(i\)个武将的最大值。

呢么对于第\(i\)行第\(j\)列我们读进来的武力值\(x\)既是第\(i\)个武将的武力值，又是第\(i+j\)个武将的武力值。

呢么就可以

if(x > f[i][1]) f[i][0] = f[i][1],f[i][1] = x;//如果x大于最大值，呢么当前的最大值就是该武将的次大值。
else if(x > f[i][0]) f[i][0] = x;//如果x只大于次大值，呢么x就是新的次大值

通过这个方法我们就可以避免排序这个复杂又耗时的过程

#include <bits/stdc++.h>
using namespace std;


const int N = 505;
int n,maxx = 0,f[N][2] = {};


inline int read()
{
	register int x = 0;
	register char ch = getchar();
	while(ch < '0' || ch > '9') ch = getchar();
	while(ch >= '0' && ch <= '9')
	{
		x = (x<<3)+(x<<1) + ch-'0';
		ch = getchar();
	}
	return x;
}



int main()
{
	n = read();
	
	for(register int i = 1;i <= n;i++)
	{
		for(register int j = 1;j <= n-i;j++)
		{
			register int x = read();
			if(x > f[i][1]) f[i][0] = f[i][1],f[i][1] = x;
			else if(x > f[i][0]) f[i][0] = x;
			
			if(x > f[i+j][1]) f[i+j][0] = f[i+j][1],f[i+j][1] = x;
			else if(x > f[i+j][0]) f[i+j][0] = x;
		}
	}
	
	for(register int i = 1;i <= n;i++) maxx = max(maxx,f[i][0]);
	printf("1\n%d\n",maxx);
	return 0;
}

Luogu P1939 矩阵加速

矩阵快速幂的模板题，推到过程很简单

\[\begin{matrix}a[i] = 1\times a[i-1] + 0\times a[i-2]+1\times a[i-3]\\ a[i-1] = 1\times a[i-1] + 0\times a[i-2]+0\times a[i-3]\\ a[i-2] = 0\times a[i-1] + 1\times a[i-2]+0\times a[i-3]\\ \Downarrow \\ \begin{bmatrix}f[i]\\f[i-1]\\f[i-2]\end{bmatrix}=\begin{bmatrix}1&0&1\\1&0&0\\0&1&0\end{bmatrix}\times \begin{bmatrix}f[i-1]\\f[i-2]\\f[i-3]\end{bmatrix}\end{matrix} \]

直接暴力矩阵快速幂是可以过的，但有没有优化呢？

我们考虑离线来做这道题

首先我们把所有的数据读入，然后离散化，并排序

对与\(ans_i\)我们可以计算\(d=n_i-n_i\)得到一个差值

然后只需将\(ans_{i-1}\)乘上状态转移矩阵\(f\)的\(d\)次方，就是\(ans_i\)

可以通过这种操作来减少多次重复的运算

#include <bits/stdc++.h>
#define LL long long
using namespace std;


const int N = 105 , M = 5 , mod = 1e9 + 7;
int n , key[N] , val[N] , ans[N];

struct matrix
{
	int x , y;
	LL v[M][M];
	
	matrix() { memset( v , 0 , sizeof(v) ); }
	
	inline friend matrix operator *  (matrix a , matrix b )
	{
		register matrix cur;
		cur.x = a.x , cur.y = b.y;
		for( register int i = 1 ; i <= cur.x ; i ++ )
		{
			for( register int j = 1 ; j <= cur.y ; j ++ )
			{
				cur.v[i][j] = 0;
				for( register int k = 1 ; k <= a.y ; k ++ ) cur.v[i][j] = ( cur.v[i][j] + a.v[i][k] % mod * b.v[k][j] % mod ) % mod;
			}
		}
		return cur;
	}
} f , res;


inline LL read()
{
	register LL x = 0;
	register char ch = getchar();
	while( ch < '0' || ch > '9' ) ch = getchar();
	while( ch >= '0' && ch <= '9' )
	{
		x = ( x << 3 ) + ( x << 1 ) + ch - '0';
		ch = getchar();
	}
	return x;
}

inline void matrix_I( matrix &t , int k)//构造单位矩阵
{
	t.x = t.y = k;
	for( register int i = 1 ; i <= k ; i ++ ) t.v[i][i] = 1;
}

inline matrix matrix_power( matrix x , int k )//矩阵快速幂
{
	if( k == 1 ) return x;
	register matrix t; matrix_I( t , 3 );
	while( k )
	{
		if( k & 1 ) t = t * x ;
		x = x * x;
		k >>= 1;
	}
	return t;
}

inline void init()
{
	f.x = f.y = 3;
	memset( f.v , 0 , sizeof( f.v ) );
	f.v[1][1] = f.v[1][3] = f.v[2][1] = f.v[3][2] = 1 ;
}


int main()
{
	n = read();
	for( register int i = 1 ; i <= n ; i ++ ) key[i] = val[i] = read();
	sort( val + 1 , val + 1 + n ) ;
	for( register int i = 1 ; i <= n ; i ++ ) key[i] = lower_bound( val + 1 , val + 1 + n , key[i] ) - val;
	res.x = 3 , res.y = res.v[1][1] = res.v[2][1] = res.v[3][1] = 1;
	val[0] = 3;
	for( register int i = 1 ; i <= n ; i ++ )
	{
		if( val[i] <= 3 ) { ans[i] = 1 , val[i] = 3 ; continue; }
		register int d = val[i] - val[ i - 1 ];//计算差值
		if( d == 0 ) //特殊情况
		{
			ans[i] = ans[ i - 1 ] ;
			continue;
		}
		init();//初始化 矩阵f 
		f = matrix_power( f , d );
		res = f * res;
		ans[i] = res.v[1][1] % mod;
	}
	for( register int i = 1 ; i <= n ; i ++ ) printf( "%d\n" , ans[ key[i] ] );
	return 0;
}

P2397 yyy loves Maths VI (mode)

Luogu P2397 yyy loves Maths VI (mode)

首先请考虑最基本的摩尔投票问题，找出一组数字序列中出现次数大于总数1/2的数字（并且假设这个数字一定存在）。显然这个数字只可能有一个。

摩尔投票算法是基于这个事实：每次从序列里选择两个不相同的数字删除掉（或称为“抵消”），最后剩下一个数字或几个相同的数字，就是出现次数

大于总数一半的那个。请首先认同这个事实，这里不证明了~

作者：喝七喜

链接：https://www.zhihu.com/question/49973163/answer/235921864

来源：知乎

这也就是本题的核心解决方法，根据摩尔投票法，开两个变量\(ans\)和\(cnt\)

对于读入的每个数\(x\)考虑以下三个操作

  1. \(cnt = 0\) 把\(x\)赋值给\(ans\)并且\(cnt = 1\)
  2. \(x=cnt\)让\(cnt++\)
  3. \(x\ne cnt\)让\(cnt--\)

最后的\(ans\)就是结果

#include<bits/stdc++.h>
using namespace std;

int x , i , ans , cnt;

int main()
{
	cin >> i;
	for( ; i >= 1 ; i -- )
	{
		cin >> x;
		if( cnt == 0 ) ans = x , cnt = 1;
		else if( x == ans ) cnt ++;
		else if( x != ans ) cnt --;
	}
	cout << ans << endl;
	return 0;
}

题解 P1516 【青蛙的约会】

这道题，是一道挺有难度的题。

设两只青蛙跳了\(a\)步，则\(A\)蛙的坐标是\(x+ma\),\(B\)蛙的坐标是\(y+na\)

所以两只青蛙相遇的充分条件是\(x+ma-(y+na) = Lb\ (b \in Z)\)

提公因式得\((m-n)a + (x-y) = Lb\)

移项，方程两边同城\(-1\)得\((n-m)a + Lb = (x-y)\)

令\(x = (m-n)\),\(y = L\),\(d = gcd(x,y)\)

用扩展欧几里得解\(xa + yb = d\)的一组解\((a,b)\)

若\((x-y) \% d \neq 0\)或\(m = n\)无解

否则\(a\)就是我们求的一组解，但不一定是题目要求的解

所以还要对\(a\)进行操作

令\(c = (x-y)\),为了方便表示我们\(swap(x,a) \ swap(y,b)\)

呢么我们本来要解的方程式是\(ax_0+by_0 = c\)

但是我们解的方程式是\(ax_1+by_1 = d\)

对于这个方程我们同乘\(\frac{c}{d}\)得\(ax_1\frac{c}{d}+by_1\frac{c}{d} = c\)

所以对于一组\((x_1,y_1)\)符合\(ax_1+by_1 = d\),则必有一组\((x_1\frac{c}{d},y_1\frac{c}{d})\)符合\(ax_0+by_0 = c\)

又因为如果\((x,y)\)是丢番图方程的一组解则\((x-\frac{b}{d} ,y+\frac{a}{d})\)也是一组解

所以如果我们知道\(x\)是一个正整数解，则最小就是让\(x\)不断地的减\(\frac{b}{d}\)这个过程就相当于取模\((x_1\frac{c}{d})\% \frac{b}{d}\)

在把x,y,a,b换回来，并代入数据得\(result = (a\times(\frac{x-y}{d}) \% (\frac{L}{d})+(\frac{L}{d}))\%(\frac{L}{d})\)

coding

#include <iostream>
#define LL long long
using namespace std;


LL x,y,n,m,l;


inline LL exgcd(LL a,LL b,LL &x,LL &y)
{
	if(a == 0)
	{
		x = 0,y = 1;
		return b;
	}
	register LL d = exgcd(b%a,a,y,x);
	x -= b / a * y;
	return d;
}


int main()
{
	LL a,b,d;
	cin >> x >> y >>  m >> n >> l;
	if(n < m) swap(m,n), swap(x,y);
	d = exgcd(n-m,l,a,b);
	if((x-y) % d || m == n) puts("Impossible");
	else cout << (a*(x-y) / d % (l/d) + (l/d)) % (l/d) << endl;
	return 0;
}

题解 P2430 【严酷的训练】

P2430 严酷的训练

这道题不是一道难题，思路很简单，好久没有做DP了，重新调整一下

之所以给这道题写题解是因为这个题在代码是现实上还是比较巧妙的

首先一眼看出这是一道背包题，而且是01背包，但是对于每个物品并没有直接给出体积

所以本题的重点就在于求体积

题目给有WKY和老王的速度\(s_1\)和\(s_2\),并且保证\(s_2|s_1 (s_1\le s_2)\) 所以对于相同难度的一道题WKY要完成的时间是老王的\(k = \frac{s_2}{s_1}\)倍

对于题这道题的权值是题目直接给出的所以直接做DP就好了

coding

#include <bits/stdc++.h>
using namespace std;


const int N = 5005; 
int n,m,k,times,t[N],w[N],v[N],f[N];

struct node
{
	int w,v;
	friend bool operator < (node a,node b) {return a.v < b.v;}
}g[N];


inline int read()
{
	register int x = 0;
	register char ch = getchar();
	while(ch < '0' || ch > '9') ch = getchar();
	while(ch >= '0' && ch <= '9')
	{
		x = (x<<3) + (x<<1) + ch - '0';
		ch = getchar();
	}
	return x;
}


int main()
{
	k = read(); k = read() / k;	n = read(); m = read();	
	for(register int i = 1;i <= m;i ++) t[i] = read() * k;
	for(register int i = 1;i <= n;i ++) g[i].v = t[read()] , g[i].w = read();
	times = read();
	
	sort(g+1,g+1+n);
	
	for(register int i = 1;i <= n;i ++)
	{
		for(register int j = times;j >= g[i].v;j --) f[j] = max(f[j],f[j-g[i].v] + g[i].w);
	}
	
	cout << f[times] << endl;
	return 0;
}

题解 P2421 【[NOI2002]荒岛野人】

luogu P2421 loj #10215

设\(x\)相遇，显然\(x\in N_+\)

要求最小的正整数\(M\)，使得对于任意的\(i,j(1\leq i,j\leq n)\)同余方程\(c_i+p_i\times x \equiv c_j + p_i\times x(mod\ M)\)无解或\(x>min(l_i,l_j)\)（有其中一人死掉）

观察题目发现\(n\)很小，直接枚举即可

从小到大枚举\(M\)再枚举每一组\(i,j\)解同余方程判断即可

下面就剩下如何解同余方程的问题了

首先原式可变形为\(c_i + p_i\times x = c_j + p_i\times x + M\times y\)

然后化成丢番图方程的形式\((p_i-p_j)x+My = (c_j-c_i)\)

扩展欧几里得解方程就行

多说一句这道题的形式和扩展中国剩余定理有些相似

#include <bits/stdc++.h>
using namespace std;


const int N = 20;
int n,m = -1,c[N],p[N],l[N];


inline int read()
{
	register int x = 0;
	register char ch = getchar();
	while(ch < '0' || ch > '9') ch = getchar();
	while(ch >= '0' && ch <= '9')
	{
		x = (x<<3)+(x<<1) + ch-'0';
		ch = getchar();
	}
	return x;
}


inline int exgcd(int a,int b,int &x,int &y)
{
	if(!a)
	{
		x = 0,y = 1;
		return b;
	}
	register int d = exgcd(b%a,a,y,x);
	x -= b / a * y;
	return d;
}

inline int gcd(int a,int b){return (!a?b:gcd(b%a,a));}

inline bool check(int k)
{
	register int a,b,x,y,d,C;
	
	for(register int i = 1;i <= n;i ++)
	{
		for(register int j = i + 1;j <= n;j ++)
		{
			a = p[i]-p[j]; b = k; C = c[j]-c[i];
			d = exgcd(a,b,x,y);
			if(C % d) continue;
			a /= d; b/= d; C /= d;
			b = abs(b);
			x = (x * C % b + b) % b;
			if(!x) x = b;
			if(x <= min(l[i],l[j])) return 1;
		}
	}
	return 0;
}


int main()
{
	n = read();
	for(register int i = 1;i <= n;i ++)
	{
		c[i] = read(); p[i] = read();l[i] = read();
		m = max(m,c[i]);
	}
	for(register int i = m;i;i ++)
	{
		if(check(i)) continue;
		cout << i << endl;
		break;
	}
	return 0;
}

题解 CF7E 【Defining Macros】

本题按照我写题的全过程再写

首先看到题面，我知道要处理运算优先级的问题

所以对于宏定义中的每个运算我开一个\(map\)分别记录他的加减号，乘除号时候被括号括起来

在表达式中错误情况有三种

  1. 前面是减号或乘除号，但后面的宏定义所有的加减没有被括起来
  2. 前面是除号，但后面宏定义所有的乘除号没有被括起来
  3. 前面是加减号没有被括起来的宏定义，后面是乘除号

当我们遍历到运算符时查看上一个相邻的时表达式还是宏定义，若是宏定义检查3

当我们遍历到宏定义时查看上一个相邻的是否是运算符，若是运算符检查1，2

然后就是处理括号的问题

我们对于括号的情况进行递归判断就好，若左括号递归到下一层，若右括号回溯到上一层

在计算表达式时，只要发现错误无论在那一层直接输出结果并exit(0)

然后我发现表达式中出现了变量（是字母，但并不是宏定义）

1
#define k ( a + b )
v/k

由于我用的是\(map\)，所以一旦遍历到字母我就利用\(find()\)函数判断是否是宏定义，如果是个变量就当作数字处理

然后还会有宏定义套宏定义的形式

#define sum x + y
#define mul a * sum

处理方法和表达式类似，要注意括号的形式

#define sum x + y 
#define mul a * ( sum )

此时递归操作比较困难，我采用了四个变量aa,bb,cc,dd分别表示上一个操作符是什么，判断即可

所以出现了第四种错误

  1. 宏定义本身是错误的

但是会有这种情况

2
#define sum x + y
#define mul x * sum
sum + sum

本身没有调用错误的宏定义，所以对于每个宏定义，我在用一个\(map\)储存这个宏定义时候是正确的，在计算表达式的时候，顺便检查宏定义时候是正确的

然后本题还有些坑点

  1. # define s+y这类的有多余的空格所以不能从第\(8\)个位置直接开始运算，要逐一遍历
  2. n=0这种情况特判即可
#include <bits/stdc++.h>
#define PBB pair< bool , bool >
#define F first 
#define S second
#define NO ("Suspicious")
#define STOP {puts(NO) , exit(0);}
using namespace std;


int n , bra , len;
string s , name , null;
map< string , PBB > def;
map< string , bool > vis; 

inline int work(int star )
{
	bool mul , add , del , dive , expr ; mul = add = del = dive = expr = 0;
	for( register int i = star , t ; i < len ; i ++ )
	{
		if( s[i] == ')' ) return i;
		if( s[i] == '(' ) { i = work( i + 1 ); add = del = dive = mul = 0; continue;}
		if( s[i] == ' ' ) continue ;
		if( s[i] >= '0' && s[i] <= '9' ) { add = del = dive = mul = 0; continue; }
		if( s[i] == '+' ) { add = 1 , expr = 0; continue; }
		if( s[i] == '-' ) { del = 1 , expr = 0; continue; }
		if( s[i] == '*' )
		{
			if( expr && !def[name].F ) STOP;
			mul = 1 , expr = 0;
			continue;
		}
		if( s[i] == '/' )
		{
			if( expr && ( !def[name].F  ) ) STOP;
			dive = 1 , expr = 0;
			continue;
		}
		
		name = null;
		if( !expr ) name = null ;
		while( s[i] != ' ' && s[i] != '+' && s[i] != '-' && s[i] != '*' && s[i] != '/' && s[i] != ')' && s[i]!= '(' && i < len) name += s[i] , i ++ ; i--;
		
		if( def.find(name) == def.end() )
		{
			add = del = mul = dive = 0;
			
			continue;
		}
		if( !vis[name] ) STOP;
		expr = 1;
		if( del && !def[name].F ) STOP;
		if( ( mul || dive ) && !	def[name].F) STOP;
		if( dive && !def[name].S ) STOP;
		add = del = mul = dive = 0;
	}
	return 0;
}

int main()
{
	cin >> n;
	if( n == 0 ) puts("OK") , exit(0);
	getline( cin , s );
	bool add , mul , aa , bb , cc , dd , ac ;
	string cur;
	for( register int t , l ; n ; n -- )
	{
		getline( cin , s ) , len = s.size();
		l = 0;
		while( s[l] != 'd') l ++;
		l += 6;
		while( s[l] == ' ' ) l ++;
		t = l;
		while( s[t] != ' ' ) t ++;
		name = s.substr( l , t - l ) , add = 1 , mul = 1;
		aa = bb = cc = dd = 0 , ac = 1 ;
		for( t ++ ; t < len ; t ++ )
		{
			if( s[t] == '(' ) { bra ++; aa = bb = cc = dd = 0; continue; }
			if( s[t] == ')' ) { bra --; aa = bb = cc = dd = 0; continue; }
			if( s[t] == '+' ) aa = 1 , bb = cc = dd = 0;
			if( s[t] == '-' ) bb = 1 , aa = cc = dd = 0;
			if( s[t] == '*' ) cc = 1 , aa = bb = dd = 0;
			if( s[t] == '/' ) dd = 1 , aa = bb = cc = 0;
			if( !bra && ( s[t] == '+' || s[t] == '-' ) ) add = 0;
			if( !bra && ( s[t] == '*' || s[t] == '/' ) ) mul = 0;
			if( s[t] >= '0' && s[t] <= '9' ) aa = bb = cc = dd = 0;
			if( ( s[t] >= 'a' && s[t] <= 'z' ) || ( s[t] >= 'A' && s[t] <= 'Z' ) )
			{
				cur = null;
				while(s[t] != ' ' && s[t] != '+' && s[t] != '-' && s[t] != '*' && s[t] != '/' && s[t] != '(' && s[t] != ')' && t < len ) cur += s[t] , t ++;
				t -- ;
				if( def.find( cur ) != def.end() )
				{
					if( ( bb || cc || dd ) && !def[cur].F ) ac = 0;
					if( !vis[cur] ) ac = 0; 
					if( !bra && def[cur].F ) add = 0;
					if( !bra && def[cur].S ) mul = 0;
				}
			}
		}
		def.insert( { name , { add , mul } } );
		vis.insert( { name , ac } );
	}
	
	getline( cin , s ) , len = s.size();
	work(0);
	puts("OK");
	return 0;
}

[POI2006]OKR-Periods of Words 题解

题目链接[POI2006] OKR-单词周期

题意

对于一个给定的字符串\(S\),如果字符串\(A\)是\(S\)前缀，且\(S!=A\),则\(A\)是\(S\)的真前缀

对于一个字符串\(T\),若\(Q\)是\(T\)的真前缀，且\(T\)是\(QQ\)（把\(Q\)复制一遍）的普通前缀，则\(Q\)是\(T\)的周期

现在给定一个字符串，求这个字符串所有前缀最大周期的长度和

思路

首先要知道KMP里一个字符串\(i\)，\(next[i]\)满足既是\(i\)的前缀又是\(i\)的后缀

同时\(next[next[i]]\)也满足这个性质，所以只要不断的找下去就可以找到\(i\)的最小前缀

然后看这张图

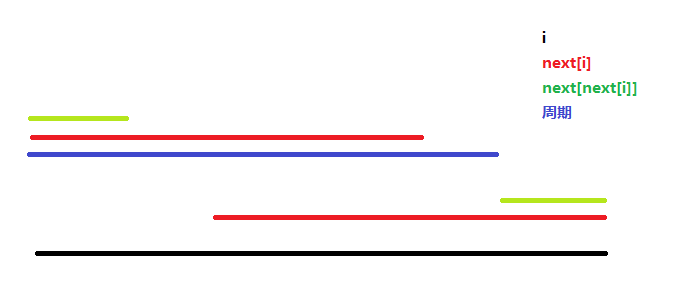
然后我们令\(j=next[i]\)做这样一件事while(next[j]) j = next[j]

经过循环后\(j\)就是\(i\)最小前缀

所以\(i\)的最大周期就是\(i-j\)

最后求和就好

#include <bits/stdc++.h>
using namespace std;

const int N =1000005;
int n,next[N];
long long cnt = 0;
char a[N];


int main()
{   
    scanf("%d%s",&n,a+1);
    register int j = 0;
    for(register int i = 1;i < n;i ++)
    {
    	while(j && a[j+1] != a[i+1]) j = next[j];
    	if(a[i+1] == a[j+1]) j++;
    	next[i+1] = j;
	}
    
    for(register int i = 2;i <= n;i ++)
    {
        j = i;
        while(next[j]) j = next[j];
        if(next[i] != 0) next[i] = j;
        cnt += i - j;
    }
    printf("%lld\n",cnt);
    return 0;
}

[SCOI2007]排列 题解

题目链接

这道题的其实也可以用数学知识来解，不过需要高中数学

30分

\(s\le5\)，那么枚举\(0\)到\(99999\)，判断每个数字和输入的是否相同就行了

50分

50分没有什么准确的做法，应该是暴力写的好或者是正解写的丑的

Part.1

先说说我们今天比赛时一个不认识的dalao的做法
他把每个序列进行排序构造出\(MAX\)和\(MIN\),在这个范围内做30分的做法就行

代码应该可是实现我就不贴了

Part.2

我自己的做法

首先我观察到如果去枚举序列，复杂度会很高

我们考虑枚举d的整数倍，在考虑是否能够被构造出来

怎么判断能否被构造呢

先开一个桶，把序列中每个数字出现的次数存下来

对于每次枚举出来的d的倍数，另开一个桶用相同的方式分解

然后比较两个桶，如果两个同相同这这个数可以被构造出来

然后我发现过\(d=1\)时这种方法会T飞

所以当\(d=1\)时我们考虑组合数给他算出来

首先假设序列长为\(n\),桶用\(t_i\)表示，就可以推出方案数为

\[\frac{A_n^n}{\Pi_{i=0}^{9}A_{ti}^{ti}} \]

然后我又发现假如\(d=2\)时，方案数只和末位奇偶有关

假设序列长为\(n\),桶用\(t_i\)表示，偶数个数为\(m\),就可以推出方案数为

\[\frac{A_{n-1}^{n-1}\times A_m^m}{\Pi_{i=0}^{9}A_{ti}^{ti}} \]

用这种方法同时可以推出\(d=5\)和\(d=10\)的情况，另外假如全是0，则只有一种情况

#include <bits/stdc++.h>
using namespace std;


const int N = 13;
int T,t[N],a[N],n,m,k,maxn;
int cnt,x;
bool flag;
string s;


inline void work_1()
{
    cnt = 1;
    for(register int i = 2;i <= n;i ++) cnt *= i;
    for(register int i = 0;i <= 9;i ++)
    {
        if(!t[i]) continue;
        for(register int j = 2;j <= t[i];j ++) cnt /= j;
    }
    printf("%d\n",cnt);
}

inline void work_2()
{
    cnt = 0;
    for(register int i = 0;i <= 9; i += 2) 
    {
        if(t[i] > 0) cnt +=t[i];
    }
    if(!cnt)
    {
        puts("0");
        return ;
    }
    for(register int i = 2;i < n;i ++) cnt *= i;
    for(register int i = 0;i <= 9;i ++)
    {
        if(!t[i]) continue;
        for(register int j = 2;j <= t[i];j ++) cnt /= j;
    }
    printf("%d\n",cnt);
}

inline void work_3()
{
    cnt = t[5] + t[0];
    if(!cnt)
    {
        puts("0");
        return ;
    }
    for(register int i = 2;i < n;i ++) cnt *= i;
    for(register int i = 0;i <= 9;i ++)
    {
        if(!t[i]) continue;
        for(register int j = 2;j <= t[i];j ++) cnt /= j;
    }
    printf("%d\n",cnt);
}

inline void work_4()
{
    cnt = t[0];
    if(!cnt)
    {
        puts("0");
        return ;
    }
    for(register int i = 2;i < n;i ++) cnt *= i;
    for(register int i = 0;i <= 9;i ++)
    {
        if(!t[i]) continue;
        for(register int j = 2;j <= t[i];j ++) cnt /= j;
    }
    printf("%d\n",cnt);
}

int main()
{
    cin >> T;
    while(T--)
    {
        memset(t,0,sizeof(t));
        cin >> s >> k;
        n = s.size();
        for(register int i = 0;i < n;i ++) t[s[i] - '0'] ++;
        m = n - t[0];
        if(!m)
		{
			puts("1");
			continue;
		}
       	if(k == 1)
        {
            work_1();
            continue;
        } 
        if(k == 2)
        {
            work_2();
            continue;
        }
        if(k == 5)
        {
            work_3();
            continue;
        }
        if(k == 10)
        {
            work_4();
            continue;
        }
        cnt = maxn = 0;
        for(register int i = 9;i >= 0;i --)
        {
            for(register int j = 1;j <= t[i];j ++) maxn = (maxn<<3)+(maxn<<1) + i;
        }
        for(register int i = 1;i * k <= maxn;i ++)
        {
		    x = i * k; flag = 1; memset(a,0,sizeof(a));
            while(x >= 9) a[x % 10] ++,x /= 10;
            a[x] ++;
            for(register int j = 1;j <= 9;j ++)
            {
                if(t[j] == a[j]) continue;
                flag = 0;
                break;
            }
            if(flag) 
			{
				cnt ++;
			}
        }
        printf("%d\n",cnt);
    }
}

100分

\(s\)的长度不会超过\(10\)

若没有重复的数字，则所有可能情况为\(362880\)

若有所有重复的数字，则所有情况不会超过\(362880\)

又\(T\le 15\)，所有情况不会超过\(5443200<10^8\)

所以此题正解为勇敢暴力，枚举即可，不用剪枝

暴力枚举所有的序列，枚举序列可以用next_permutation()

#include <bits/stdc++.h>
using namespace std;


const int N = 13,mod = 19260817;
int T,cnt,k,len,a[N];
long long sum;
string s;


int main()
{
	cin >> T;
	while(T --)
	{
		cin >> s >> k;
		len = s.size();cnt = 0;
		for(register int i = 1;i <= len;i ++) a[i] = s[i-1] - '0';
		sort(a+1,a+1+len);
		do
		{	
			sum = 0;
			for(register int i = 1;i <= len;i ++) sum = (sum<<3)+(sum<<1)+a[i];
			if(sum % k == 0) cnt ++; 
		}while(next_permutation(a+1,a+1+len));
		printf("%d\n",cnt);
	}
}

题解 P1577 【切绳子】

原题连接P1577 切绳子

首先这是一道很常规的二分题看标签就知道了

思路很常规，二分答案贪心判断

首先假设第\(i\)个绳子长度为\(a[i]\)呢么这条绳子说能切割出的绳子条数为$\frac {a[i]} {mid} $,求和判断一下就好了

看到这里你是不是觉得写完了

不 \(o(>﹏<)o\) 这道题卡精度，想不到吧！！！

如果你\(85\)分\(WA\)，呢么恭喜\(printf\)四舍五入卡住了您

如果你\(92\)分\(RE\)，呢么恭喜您您的除数出现了\(0\)

呢么我就说说我是怎么解决这两个问题的

第一个，我发现数据很水所以读入时每个数乘\(100\)输出时在除\(100\)就好了

第二个，在二分时加一个 if(!mid) break;

\(85\)分\(WA\) \(coding\)

#include <bits/stdc++.h>
using namespace std;


const double e = 1e-3;
const int N = 10005;
int n,m,cnt;
double a[N] = {},l,r,result;


inline bool check(double k)
{
    cnt = 0;
    for(register int i = 1;i <= n;i ++)
    {
        cnt += a[i]/k;
        if(cnt > m) return 1;
    }
    return cnt >= m;
}


int main()
{
    scanf("%d%d",&n,&m);
    for(register int i = 1;i <= n;i ++)
    {
        scanf("%lf",&a[i]);
        r += a[i];
    }
    r /= m*1.0;
    while(l + e < r)
    {
        register double mid = (r+l)/2;
        if(check(mid)) l = mid,result = mid;
        else r = mid;
    }
    printf("%.2lf\n",result);
    return 0;
}

\(92\)分\(RE\) \(coding\)

#include <bits/stdc++.h>
using namespace std;


const int N = 10005;
int n,m,cnt;
int a[N] = {},l,r = 1 << 30,result;
double num;


inline bool check(int k)
{
    cnt = 0;
    for(register int i = 1;i <= n;i ++)
    {
        cnt += a[i]/k;
        if(cnt > m) return 1;
    }
    return cnt >= m;
}


int main()
{
    scanf("%d%d",&n,&m);
    for(register int i = 1;i <= n;i ++)
    {
        scanf("%lf",&num);
        a[i] = num*100;
    }
    while(l <= r)
    {
        register int mid = (r+l)>>1;
        if(check(mid)) l = mid+1;
        else r = mid-1;
    }
    printf("%.2lf\n",r/100.0);
    return 0;
}

\(ACcoding\)

#include <bits/stdc++.h>
using namespace std;


const int N = 10005;
int n,m,cnt;
int a[N] = {},l,r = 1 << 30,result;
double num;


inline bool check(int k)
{
    cnt = 0;
    for(register int i = 1;i <= n;i ++)
    {
        cnt += a[i]/k;
        if(cnt > m) return 1;
    }
    return cnt >= m;
}


int main()
{
    scanf("%d%d",&n,&m);
    for(register int i = 1;i <= n;i ++)
    {
        scanf("%lf",&num);
        a[i] = num*100;
    }
    while(l <= r)
    {
        register int mid = (r+l)>>1;
        if(!mid) break;
        if(check(mid)) l = mid+1;
        else r = mid-1;
    }
    printf("%.2lf\n",r/100.0);
    return 0;
}

题解 P1296 【奶牛的耳语】

首先这道题最弱的方法就是枚举，\(sort()\)排序后两层\(for()\)循环扫一遍在逐一判断就好

但是排序后，如果\(a[j]-a[i]\leqslant dis\)

则\(a[j]-a[i+1]\leqslant dis\)也一定成立

所以\(j\)并不用从头开始

coding

#include <bits/stdc++.h>
using namespace std;


const int N = 1e6 + 5;
int n,result = 0,dis,a[N] = {};


inline int read()
{
	register int x = 0;
	register char ch = getchar();
	while(ch < '0' || ch > '9') ch = getchar();
	while(ch >= '0' && ch <= '9')
	{
		x = (x<<3)+(x<<1) + ch-'0';
		ch = getchar();
	}
	return x;
}


int main()
{
	n = read(); dis = read();
	for(register int i = 1;i <= n;i ++) a[i] = read();
	
	sort(a+1,a+1+n);
	
	register int j = 2;
	for(register int i = 1;i <= n;i ++)
	{
		while(j <= n && a[j] - a[i] <= dis) j ++;
		j --;
		result += j - i;
	}
	
	printf("%d\n",result);
	return 0;
}

NOI 2009 食物链

Luogu P2024 [NOI2001]食物链

并查集对没有错就是并查集

查找、合并的过程与普通并查集没什么差别。

我们定义 \(f[i]\)是同类

\(f[i+n]\)吃\(i\)

\(f[i+2*n]\)被\(i\)吃

紧接着就是判断

int a,b;
if(getfather(a) == getfather(b))//a b 同类
if(getfather(a) == getfather(b+n))// a 吃 b
if(getfather(a) == getfather(b+2*n)) // b 吃 a

通过这个方法来判断每局话真假就好

coding

#include <bits/stdc++.h>
using namespace std;


const int N = 150015;
int n,k,cnt = 0,fa[3*N] = {},d,a,b;


inline int read()
{
	register int x = 0;
	register char ch = getchar();
	while(ch < '0' || ch > '9') ch = getchar();
	while(ch >= '0' && ch <= '9')
	{
		x = (x<<3)+(x<<1) + ch-'0';
		ch = getchar();
	}
	return x;
}

inline int getfather(int x)
{
	if(x == fa[x]) return x;
	return fa[x] = getfather(fa[x]);
}

inline void bing(int x,int y)
{
	x = getfather(x); y = getfather(y);
	fa[x] = y; 
}


int main()
{
	n = read(); k = read();
	for(register int i = 1;i <= 3*n;i++) fa[i] = i;
	for(;k >= 1;k--)
	{
		d = read(); a = read(); b = read();
		if(a > n || b > n || (d == 2 && a == b))
		{
			cnt++;
			continue;
		}
		if(d == 1)
		{
			if(getfather(a+n) == getfather(b) || getfather(a+2*n) == getfather(b))
			{
				cnt++;
				continue;
			}
			bing(a,b); bing(a+n,b+n); bing(a+2*n,b+2*n);
		}
		else
		{
			if(getfather(a) == getfather(b) || getfather(a+n) == getfather(b))
			{
				cnt++;
				continue;
			}
			bing(a+2*n,b); bing(a+n,b+2*n); bing(a,b+n);
		}
	}
	printf("%d\n",cnt);
	return 0;
}

Luogu P1113 杂务

首先对于每一件事开始之前都必须先完成之前的\(k\)个准备工作，所以对于当前事件的最优开始时间就是\(k\)个准备工作中最晚的结束时间。因为工人无限多。

呢么完成所有时间对最短时间就是最后一件事的结束时间。

#include <bits/stdc++.h>
using namespace std;


const int N = 10005;
int n,f[N] = {},t = 0,k,cnt;

inline int read()
{
	register int x = 0;
	register char ch = getchar();
	while(ch < '0' && ch > '9') ch = getchar();
	while(ch >= '0' && ch <= '9')
	{
		x = (x<<3)+(x<<1) + ch-'0';
		ch = getchar();
	}
	return x;
}


int main()
{
	n = read();
	for(register int i = 1;i <= n;i++)
	{
		read(); cnt = read(); k = read();
		while(k) f[i] = max(f[i],f[k]),k = read();
		f[i] += cnt;
		t = max(t,f[i]);
	}
	printf("%d\n",t);	
	return 0;
}

[AHOI2009]维护序列 题解

[AHOI2009]维护序列

【模板】线段树 2

这两题基本相同，所以就放在一起讲

题目

维护一个序列，要求支持一下三种操作

  1. 区间加一个数
  2. 区间乘一个数
  3. 区间求和

solution

首先这是线段数，不要问为什么。 因为很显然

我们都知道线段树的一个基操，就是懒惰标记

这道题我们需要维护两个懒惰标记\(add\)和\(mul\)

对于一个区间的值我们用\(value\times mul + (r-l+1)\times add\)来表示

区间加\(x\)就可以表示为\(value \times mul + (r-l+1)\times (add + x)\)

也即把\(add\)标记变为\(add+x\)

区间乘\(x\)就可以表示为\(value \times mul \times x + (r-l+1)\times add \times x\)

也即把\(add\)标记变为\(add\times x\)，把\(mul\)标记变为\(mul\times x\)

这里要注意一点因为运算的优先级所以要先维护mul再维护add

coding

#include <bits/stdc++.h>
#define LL long long
using namespace std;


const int N = 100005;
LL n,m,p,a[N];

struct Node
{
    LL l,r,value,mul,add;
    Node * left , * right;
    Node(LL s , LL t , LL v , Node * a , Node * b)
    {
        l = s , r = t , value = v , mul = 1 , add = 0;
        left = a , right = b;
    }
} * root;


inline LL read()
{
    register LL x = 0;
    register char ch = getchar();
    while(ch < '0' || ch > '9') ch = getchar();
    while(ch >= '0' && ch <= '9')
    {
        x = (x<<3)+(x<<1) + ch-'0';
        ch = getchar();
    }
    return x;
}


inline Node * build( LL l , LL r)
{
    if(l == r) return new Node( l , r , a[l] % p,0 , 0 );
    register LL mid = ( l + r) >> 1;
    Node * left = build( l , mid ) , * right = build( mid + 1 , r);
    return new Node(l , r , (left -> value + right -> value) % p , left , right);
}

inline LL get_value(Node * cur)
{
	return ( cur -> value * cur -> mul + cur -> add * (cur -> r - cur -> l + 1) ) % p;
}

inline void mark(LL add , LL mul , Node * cur)
{	
	
	cur -> add = ( cur -> add * mul + add ) % p;
	cur -> mul = ( cur -> mul * mul) % p;
	cur -> value = (cur -> value * mul + ( cur -> r - cur -> l + 1) * add ) % p;
	//这里要注意修改去区间的值不能用标记的值，要用增加的值 
	return ;
}


inline void pushdown( Node * cur)
{
	if(cur -> mul == 1 && cur -> add == 0) return ;
    if(cur -> left)//如果有儿子节点，不是叶子节点 
    {
        mark( cur -> add , cur -> mul , cur -> left);
        mark( cur -> add , cur -> mul , cur -> right);
    }
    else cur -> value = cur -> value * cur -> mul + cur -> add;
    //如果是叶子节点这不用标记下传，直接修改 
	cur -> mul = 1; cur -> add = 0;
	//下传后情况标记 
	return ;
}

inline LL query( LL l , LL r , Node * cur)
{
	if( l <= cur -> l && cur -> r <= r) return cur -> value % p;
    register LL mid = (cur -> l + cur -> r) >> 1, res = 0;
    pushdown( cur );
    //因为要访问子节点所以先把标记下传 
    if( l <= mid ) res += query( l , r , cur -> left) % p;
    if( mid + 1 <= r ) res += query( l , r , cur -> right) % p;
    return res % p;
}

inline void modify( LL l , LL r , LL add , LL mul , Node * cur)
{
	if(cur -> l > r || cur -> r < l) return ;
	if(l <= cur -> l && cur -> r <= r)
	{
		mark( add , mul , cur);
		return ;
	}
	if( cur -> add != 0 || cur -> mul != 1 ) pushdown( cur );
	//因为要访问子节点所以先把标记下传 
	register LL mid = (cur -> l + cur -> r) >> 1;
	if( l <= mid ) modify( l , r , add , mul , cur -> left);
	if( mid + 1 <= r ) modify( l , r , add ,mul , cur -> right);
	cur -> value = ( cur -> left -> value + cur -> right -> value) % p;
	//用子节点的值更新当前区间的值 
}

int main()
{
    n = read();m = read(); p = read();
    for(register int i = 1 ; i <= n ; i ++) a[i] = read();
    root = build( 1 , n );
    
    while( m -- )
    {
    	register LL opt = read();
        if( opt == 1 )
        {
            register LL l = read() , r = read() , v = read();
            modify( l , r , 0 , v , root );
        }
        else if( opt == 2)
        {
            register LL l = read() , r = read() , v = read();
            modify( l , r , v , 1 , root );
        }
        else 
        {
            register LL l = read() , r = read();
            printf("%lld\n", query( l , r , root ));
        }
    }
    return 0;
}

题解 P4702 【取石子】

看了一下之前的大佬们写的题解，思路非常清晰，很容易推断出就是对所有的石子数求和在判断一下奇偶即可。但是看到各大佬们的代码，我想说其实不用开\(long long\),因为决定一个数奇偶的只有个位，再准确点就是二进制下的第一位，所以每次求和后\(Mod10\)就可以了

#include<bits/stdc++.h>
using namespace std;


int n,x,sum;


int main()
{
    scanf("%d",&n);
    for(int i = 1;i <= n;i++)
    {
        scanf("%d",&x);
        sum += x;
        sum %= 10;
    }
    if(sum & 1) puts("Alice");
    else puts("Bob"
    return 0;
}

Luogu P3150 pb的游戏

首先呢这一道博弈论，说实话博弈论我也不会

所以这篇题解也就是提供一个大概的思路，并没有严格的证明

首先\(N\)的范围很小，我们就是不考虑了，就当是个常数吧

呢么对于每一轮游戏来说，都有\(k\)次回合，所以我们对于每次回合来说就好了

如果\(m=2\)呢么我们都选择就只能是把他分成两个\(1\)

如果\(m=1\)呢么就不能继续分解也就是说这个回合的人输了

由于两个人都是“聪明绝顶”，所以对于自己的回合一定是会分解出一个让对手必输的数也就是\(1\)

所以对于一个数\(m\),两个人的选择都是把这个数分解成\(m-1\)和\(1\)

呢么对已一开始的数\(m\)如果是偶数后手一定赢，反之先手赢

先手每次都是\(pb\),所以这就是一道判断奇偶数的题

coding

#include <bits/stdc++.h>
using namespace std;


inline int read()
{
	register int x = 0;
	register char ch = getchar();
	while(ch < '0' || ch > '9') ch = getchar();
	while(ch >= '0' && ch <= '9')
	{
		x = (x<<3)+(x<<1) + ch-'0';
		ch = getchar();
	}
	return x;
}

int main()
{
	for(register int i = read();i >= 1;i--)
	{
		register int x = read();
		if(x&1) puts("zs wins");
		else puts("pb wins");
	}
	return 0;
}

Luogu P1007 独木桥

P1007 独木桥

我们首先考虑只有一个人的情况，呢么他下桥的方式只有两种

  1. 向起点走,时间为 x (x是当前人的位置)
  2. 向终点走,时间为 L+1-x

显然对于这种情况下我们只要对这两种方案取\(min\)和\(max\)就是最小时间和最大时间

好的，我们考虑两个人的情况

如果两人同向运动，因为速度相同也就不可能相遇且间距保持不变。初中物理

再说相向运动，记住你自己并不在桥上，你在桥下。假如你知道了敌军的轰炸所以你提前跑的了离桥很远的地方用望远镜来看。你只能看到两个绿点在运动。但他们相遇时，然后又快速的转身离开了，因为转身不耗时间，呢么你看的就是两个绿点重合后又继续移动，或者说一个人代替另一个人继续行走。

哔哔了一大堆，说白了就是两人相遇没有影响所以正常处理就好了。

即最短时间就是所有人都按照自己最短的路径下桥，最后一个下桥的人所用的时间

最长时间就是所有人都按照自己最长的路径下桥，最后一个下桥的人所用的时间

coding

#include <bits/stdc++.h>
using namespace std;


int l,n,maxt = 0,mint = 0,num;


inline int read()
{
	register int x = 0;
	register char ch = getchar();
	while(ch < '0' || ch > '9') ch = getchar();
	while(ch >= '0' &&ch <= '9')
	{
		x = (x<<3)+(x<<1) + ch-'0';
		ch = getchar();
	}
	return x;
}


int main()
{
	l = read()+1; n = read();
	while(n--)
	{
		num = read();
		mint = max(mint,min(num,l-num));
		maxt = max(maxt,max(num,l-num));
	}
	printf("%d %d\n",mint,maxt);
	return 0;
}

Lougu P1827 American Heritage

题目

简明题意

给出一个树中序和前序遍历输出树的后续遍历

题解

首先会写这道题你要有一定的前置技能

  • 了解树的基本知识和树的三种遍历方法
  • 知道前序、中序或者知道后序、中序怎么求另一种序列
  • 会编程

树的三种遍历

不做过多解释

树的中序遍历是按照左子树，根，右子树的顺序访问节点。

树的前序遍历是按照根，左子树，右子树的顺序访问节点。

树的后序遍历是按照左子树，右子树，根的顺序访问节点。

还原

这是个初赛知识，简单的说一下

首先据前序的一个结点或后序的最后一个结点这个结点是当前序列的根节点

根据当前序列的根节点在中序中把树分成左右两个子树

递推下去

如果你掌握了以上几个前置技能请继续

首先根据当前序列分出左右子树和根

  1. 遍历左子树
  2. 遍历右子树
  3. 输出根

这点用\(DFS\)能非常简单的实现

coding

#include <bits/stdc++.h>
using namespace std;


string a,b;//a中序 b前序 


inline void dfs(int la,int ra,int lb,int rb)
{
	if(la > ra || lb > rb) return ;
	register int i = a.find(b[lb]);
	dfs(la,i-1,lb+1,lb+i-la);//left son
	dfs(i+1,ra,lb+i-la+1,rb);//rgiht son
	cout << a[i];
}


int main()
{
	cin >> a >> b;
	
	int len = a.size() - 1;
	
	dfs(0,len,0,len);
	
	return 0;	
}

题解 P3853 【[TJOI2007]路标设置】

原题连接P3853 [TJOI2007]路标设置

直接开始，很明显二分。为什么？感觉是

首先我们二分一下出一个答案然后判断即可，很常规的二分答案题。

呢么整道题的难点就在于怎么判断了

首先题目上说路标是按照单调递增的顺序输入所以两个相邻路标的距离就是\(x = a[i]-a[i-1]\),呢么\(\left \lfloor \frac{x}{mid} \right \rfloor\)就是两个路标之间应该放多少个新路标

所以求出一共需要放多少个新路标与\(N\)比较即可

coding

#include <bits/stdc++.h>
using namespace std;


const int N = 100005,INF = 0x7f7f7f7f;
int n,m,k,a[N],l = 0,r,result;


inline int read()
{
   register int x = 0;
   register char ch = getchar();
   while(ch < '0' || ch > '9') ch = getchar();
   while(ch >= '0' && ch <= '9')
   {
   	x = (x<<3)+(x<<1) + ch-'0';
   	ch = getchar();
   }
   return x;
}

inline bool check(int cur)
{
   register int cnt = 0;
   for(register int i = 1;i < n;i ++)
   {
   	cnt += a[i]/cur;
   	if(cnt > k) return 0;
   }
   return cnt <= k;
}


int main()
{
   r = read(); n = read(); k = read();
   for(register int i = 1;i <= n;i ++) a[i] = read();
   for(register int i = 1;i < n;i ++) a[i] = a[i+1] - a[i] - 1;
   while(l <= r)
   {
   	register int mid = (l+r)>>1;
   	if(check(mid)) r = mid - 1,result = mid;
   	else l = mid + 1;
   }
   printf("%d\n",result);
   return 0;
}

题解 P5082 成绩

如果是\(128M\)空间的话没什么好说的，直接模拟就好

现在我门考虑\(5M\)的情况

首先我们先做几个约定

Full //每一科的满分之和
Gets //每一科的实际得分之和
lose //每一科的扣分之和

首先显而易见的\(lose = Full - Gets\)

观察原始的计算式为\((Full*3 - Gets*2) / lose\)

很显然我们可以化简为\((Full + lose*2)/lose\)

把括号拆开就可以得到\(Full/lose + 2\)

到现在为止我们成功的把乘法化简掉了为什么要这么做了

我们观察\(100\%\)的数据\(n = 1e7\)

但我们并不知道一门课的总分十多少

呢么我们根据经验假设一门课时100分

呢么\(Full = 1e9\) 游走在爆精度的边缘

在根据题意\(Full * 3 = 3e9\) 成功的爆了精度

所以如果没有了乘法我们就可以用\(int\)卡过去

很显然\(Full\)和\(Gets\)只要\(for\)一边，边读入边计算就好了

coding

#include <bits/stdc++.h>
using namespace std;



int n,Full,Gets,lose;


inline int read()
{
	register int x = 0;
	register char ch = getchar();
	while(ch < '0' || ch > '9') ch = getchar();
	while(ch >= '0' && ch <= '9')
	{
		x = (x<<3)+(x<<1) + ch-'0';
		ch = getchar();
	}
	return x;
}


int main()
{
	n = read();
	for(register int i = 1;i <= n;i ++) Full += read();
	for(register int i = 1;i <= n;i ++) Gets += read();
	lose = Full - Gets;
	printf("%.6lf",1.0 * Full / lose + 2);
	return 0;
}

P1019 单词接龙

往年的\(noip\)原题，纯搜索吧，没啥可讲的，直接暴力枚举，暴力判断就行

没有必要每次都存一个很大的字符串，只要存当前的字符串就行了

每个字符串可以用两次

不能包含关系。。。好像也没啥了吧

#include <bits/stdc++.h>
using namespace std;


const int N = 23;
int n , ans = -1 , v[N] ;
string str[N];

inline int check( string s1 , string s2)
{
    register bool flag;
    for( register int i = 1 ; i < min( s1.size() , s2.size() ) ; i ++ )
    {
        flag = 1;
        for( register int j = 0 ; j < i && flag ; j ++ )
        {
            if( s1[s1.size() - i + j ] != s2[j] ) flag  = 0;
        }
        if( flag ) return i;
    }
    return 0;
}

inline void dfs( string cur , int x )
{
    ans = max( ans , x );
    for( register int i = 1 , k ; i <= n ; i ++ )
    {
        if( v[i] >= 2 ) continue;
        k = check( cur , str[i] );
        if( k )
        {
            v[i] ++;
            dfs( str[i] , x + str[i].size() - k );
            v[i] --;
        }
    }
    return ;
}

int main()
{
    cin >> n;
    for( register int i = 1 ; i <= n + 1 ; i ++ ) cin >> str[i];
    dfs( ' ' + str[ n + 1 ] , 1 );
    cout << ans << endl;
    return 0;
}

P1510 精卫填海

这也是一个经典的背包问题，背包求最小费用

f[i][j]表示前\(i\)个物品用了\(j\)的体力所能填满的最大空间，显然滚动数组优化一维空间

然后枚举一下体力，找到最先填满全部体积的一个即可

简单分析一下，当花费的体力增加时，所填满的体积保证不会减小，满足单调性

二分查找会更快

#include<bits/stdc++.h>
using namespace std;


const int N = 10005;
int n , V , power ,f[N] , use;
bool flag = 0;

inline int read()
{
    register int x = 0;
    register char ch = getchar();
    while( ch < '0' || ch > '9' ) ch = getchar();
    while( ch >= '0' && ch <= '9' )
    {
        x = ( x << 3 ) + ( x << 1 ) + ch - '0';
        ch = getchar();
    }
    return x;
}


int main()
{
    V = read() , n = read() , power = read();
    for( register int i = 1 , v , w ; i <= n ; i ++ )
    {
        v = read() , w = read();
        for( register int j = power ; j >= w ; j -- ) f[j] = max( f[j] , f[ j - w ] + v );
    }
    use = lower_bound( f + 1 , f + 1 + power , V ) - f;
    if( f[use] >= V ) printf( "%d\n" , power - use );
    else puts("Impossible");
    return 0;
}

P2918 买干草Buying Hay

类似P1510精卫填海，不过这是完全背包稍作修该即可

不过要注意f[need]并非最优解，因为可以多买点，只要比需要的多即可

#include <bits/stdc++.h>
using namespace std;

const int N = 505005 , INF = 0x7f7f7f7f;
int n , need , f[N] , ans = INF ;


inline int read()
{
    register int x = 0;
    register char ch = getchar();
    while( ch < '0' || ch > '9' ) ch = getchar();
    while( ch >= '0' && ch <= '9' )
    {
        x = ( x << 3 ) + ( x << 1 ) + ch - '0';
        ch = getchar();
    }
    return x;
}


int main()
{
    n = read() , need = read();
    memset( f , INF , sizeof(f) ) , f[0] = 0;
    for( register int i = 1 , w , v ; i <= n ; i ++ )
    {
        v = read() , w = read();
        for( register int j = v ; j <= need + 5000; j ++ ) f[j] = min( f[j] , f[ j - v ] + w ) ;
    }
    for( register int i = need ; i <= need + 5000 ;  i ++ ) ans = min( ans , f[i] );
    cout << ans << endl;
    return 0;
}

P2312 解方程

\(noip\)的原题，因为Luogu跑的比较快，所以可以用非正确算法过这道题

对于读入进来的数我们可以取一个模，为什么呢因为一个数等于0那么这个数模一个数也等于0

但是模一个数等于0的数可不一定等于0，为了尽可能的避免这种情况，要尽可能的采用一个大质数，质数越大，越不容易出现问题

然后在用秦九韶算法可以\(O(n)\)的算出结果，所以枚举每一个数\(O(n)\)的判断即可，所以总复杂度\(O(nm)\)

#include <bits/stdc++.h>
#define LL long long
using namespace std;


const int N = 105 , M = 1e6 + 5 , p = 1e9+7;
int n , m , tot , ans[M];
LL a[N];

inline void read( LL & a )
{
	register LL f = 1;
	register char ch = getchar();
	for( ; ch < '0' || ch > '9' ; ( ch == '-' ? f = - 1 : f ) , ch = getchar() );
	for( ; ch >= '0' && ch <= '9' ; a = ( ( a << 3 ) % p + ( a << 1 ) % p + ch - '0' ) % p , ch = getchar() );
	a *= f ;
	return ;
}

inline bool check( LL x )
{
	register LL s = a[n];
	for( register int i = n - 1 ; i >= 0 ; i -- ) s = ( s * x + (LL)a[i] ) % p ;
	return !s;
}


int main()
{
	cin >> n >> m;
	for( register int i = 0 ; i <= n ; read( a[i] ) , i ++ );
	
	for( register int i = 1 ; i <= m ; i ++ )
	{
		if( check( i ) ) ans[ ++ tot ] = i;
	}
	
	printf( "%d\n" , tot );
	for( register int i = 1 ; i <= tot ; printf( "%d\n" , ans[i] ) , i ++ );
	return 0;
}

P2296 寻找道路

\(Noip\)原题，首先考虑如何满足第一个条件，反向建图，充目标点开始做\(DFS\)，把所有到达的点打上标记，这样如果一个点的子节点全部都被打上标记，那么这个点就满足第一条件

第二个条件就是裸的最短路，直接在被标记的点的中跑一遍最短路

#include <bits/stdc++.h>
#define PII pair< int, int >
#define F first
#define S second
using namespace std;


const int N = 10005 , INF = 0x7f7f7f7f;
int n , m , st , ed , dis[N];
bool vis[N] , can[N];
set< PII > s;
vector<int> e[N] , t[N] ;


inline int read()
{
	register int x = 0;
	register char ch = getchar();
	while( ch < '0' || ch > '9' ) ch = getchar();
	while( ch >= '0' && ch <= '9' )
	{
		x = ( x << 3 ) + ( x << 1 ) + ch - '0';
		ch = getchar(); 
	} 
	return x;
}

inline void add( int x , int y ) { e[x].push_back(y) , t[y].push_back(x); }

inline void dfs( int x )
{
	can[x] = 1;
	for( register auto v : t[x] )
	{
		if( can[v] ) continue; 
		dfs( v );
	}
	return ;
}

inline bool panding( int x )
{
	for( register auto v : e[x] )
	{
		if( can[v] ) continue;
		return 1;
	}
	return 0;
}

inline void Dijkstra()
{
	for( register int i = 1 ; i <= n ; i ++ ) dis[i] = INF;
	s.insert( { 0 , st } ) , dis[st] = 0;
	
	for( register int u , w; s.size() ; )
	{
		u = s.begin() -> S , s.erase( s.begin() );
		if( vis[u] ) continue;
		vis[u] = 1;
		if( panding(u) ) continue;
		if( u == ed ) return ;
		for( register auto v : e[u] )
		{
			if( dis[v] <= dis[u] + 1 ) continue;
			dis[v] = dis[u] + 1;
			s.insert( { dis[v] , v } );
		}
	}
}


int main()
{
	n = read() , m = read();
	for( register int x , y ; m >= 1 ; x = read() , y = read() , add( x , y ) , m -- );
	st = read() , ed = read();
	
	dfs(ed);
	
	Dijkstra();
	
	cout << ( dis[ed] == INF ? -1 : dis[ed] ) << endl;
	return 0;
}

[Luogu P5886 Hello,2020!]题解

Luogu P5886

好久没有写题了，感觉思维有些退化，明明是到简单题却交了三遍才过

对于每个评委可以钦定多个人得第一，但是只有P个评委钦点到了真正的第一名

呢么对于真正的第一名他一定被P个评委钦定过

所以我们统计每个人被评委钦定的次数，然后统计哪些人被钦定了P次，最后依次输出即可

好吧为啥我提交了三次了，第一次我统计所以大于等于P次的人，第二次我输了一列，题目要求输出一行

emm，还是自己傻逼

其实我觉得这题可以加强一下难度，增加数据范围，并且不保证数据合法还是可以随便用个log的数据结构维护下的吧

#include <bits/stdc++.h>
using namespace std;


const int N = 1e6 + 5;
int n , m , p , f[N] , cnt ;
vector < int > ans;


inline int read()
{
	register int x = 0;
	register char ch = getchar();
	for( ; ch < '0' || ch > '9' ; ch = getchar() );
	for( ; ch >= '0' && ch <= '9' ; x = ( x << 3 ) + ( x << 1 ) + ch - '0' , ch = getchar() );
	return x;
} 


int main()
{
	n = read() , m = read() , p = read();
	for( register int i = 1 , k ; i <= n ; i ++ )
	{
		k = read();
		for( register int j = 1 , t ; j <= k ; j ++ )
		{
			t = read();
			f[t] ++;
		}
	}
	for( register int i = 1 ; i <= m ; i ++ )
	{
		if( f[i] != p ) continue;
		cnt ++;
		ans.push_back( i );
	}
	printf( "%d\n" , cnt );
	for( auto it : ans ) printf( "%d " , it );
	puts("");
	return 0;
}
posted @ 2021-07-09 17:36  PHarr  阅读(93)  评论(0)    收藏  举报