让你不可能看不明白的0-1背包代码

一、首先搞懂，什么是动态规划？

　　所谓动态规划，dynamic programming以我的短见来看不必看的太过复杂，名字的确霸气，但实际的基础应用中更像递归的高级版

　　能使用动态规划的问题有如下三个特征：

　　(1) 最优化原理：如果问题的最优解所包含的子问题的解也是最优的，就称该问题具有最优子结构，即满足最优化原理。

　　(2) 无后效性：即某阶段状态一旦确定，就不受这个状态以后决策的影响。也就是说，某状态以后的过程不会影响以前的状态，只与当前状态有关。

　　(3)有重叠子问题：即子问题之间是不独立的，一个子问题在下一阶段决策中可能被多次使用到。（该性质并不是动态规划适用的必要条件，但是如果没有这条性质，动态规划算法同其他算法相比就不具备优势）

　　

　　动态规划的解决思路：为由于整体过程直接解决过于复杂，因此把问题分割成无数小问题，在每一个小问题里得到局部最优解，因为每一步都是当下的最优解，一直递归得到的就是最终的最优解；

 

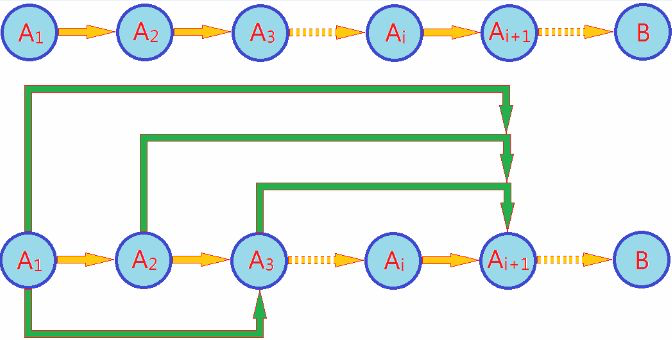
初始状态→│决策１│→│决策２│→…→│决策ｎ│→结束状态

 

 

 

二、代码步骤详解（附完整简洁代码）

#include <iostream>
using namespace std;
#define C 18                         //背包容量
#define N 7                          //物品种类为6
//默认下标从1开始
int w[N] = {0, 2, 9,  8, 6, 10, 8},   //物品重量
    v[N] = {0, 9, 3, 18, 11, 7, 12}, //物品价值
    m[N][C] = {0};                   //每一个小网格的最优解
    //容量c 种类n 子背包容量j
// Knapsack：子背包
void Knapsack(int c, int n)
{
    int jMax = w[n] - 1 < c ? w[n] - 1 : c;//这里jMax的值作用是看能不能放下，也算是剪枝了
    for (int j = 0; j <= jMax; j++)//置空前面因为放不下哈哈
        m[n][j] = 0;
    for (int j = w[n]; j <= c; j++)//从8开始到18，
        m[n][j] = v[n];//最后一行全变为12，假设一个容量为w[n]
    for (int i = n - 1; i > 1; i--) // i从最后一个开始往回，不断判断各个物品，最后i=1时不必判断，只要判断放不放即可
    {
        jMax = w[i] - 1 < c ? w[i] - 1 : c;//jMax为w[i]-1和c中小的那个，看第i件物品是不是能放进背包
        //初始化，因为i从最后一件物品往回遍历，默认把下面的网格最优解先拷贝了
        for (int j = 1; j <= jMax; j++)
            m[i][j] = m[i + 1][j];
        //判断
        for (int j = w[i]; j <= c; j++)
            m[i][j] = m[i + 1][j] > m[i + 1][j - w[i]] + v[i] ? m[i + 1][j] : m[i + 1][j - w[i]] + v[i];
    }
    m[1][c] = m[2][c];
    if (c >= w[1])
        m[1][c] = m[1][c] > m[2][c - w[1]] + v[1] ? m[1][c] : m[2][c - w[1]] + v[1];
}
// 算法的时间复杂度为O(nc)

//回溯
void Traceback(int c, int n, int x[])
{
    //这里所谓回溯不过是从头看一遍都放了哪几个，因为从下往上规划，最上面的是最优的
    for (int i = 1; i < n; i++)
        if (m[i][c] == m[i + 1][c])
            x[i] = 0;
        else
        {
            x[i] = 1;
            c -= w[i];
        }
    x[n] = m[n][c] > 0 ? 1 : 0;
}

int main()
{
    int x[N] = {0};
    Knapsack(C, N - 1);
    Traceback(C, N - 1, x);
    cout<<endl<< " C=\t" << C << endl<< " x:\t";
    int w1 = 0, v1 = 0;
    for (int i = 1; i < N; i++)
    {
        cout << x[i] << '\t';
        w1 += x[i] * w[i];
        v1 += x[i] * v[i];
    }
    cout << endl
         << "Weight=\t" << w1 << endl;
    cout << "Value=\t" << v1 << endl
         << endl;
}