广度优先搜索 BFS

<目录

广度优先搜索 \(\sf\small\color{gray}Breadth\ First\ Search\)

基本思想

广度优先搜索，个人认为，和深度优先搜索对比理解要好得多。
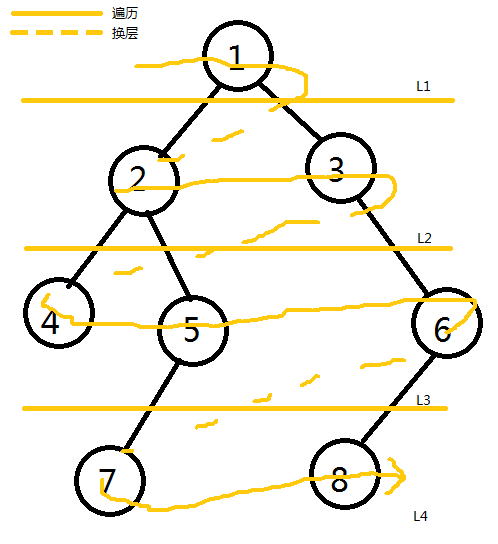
广度优先搜索，亦称层次遍历，指的是在遍历树上按照从上至下，从左至右的次序遍历整棵树。
让我们来看看 BFS 和 DFS 的遍历树吧。

BFS	DFS
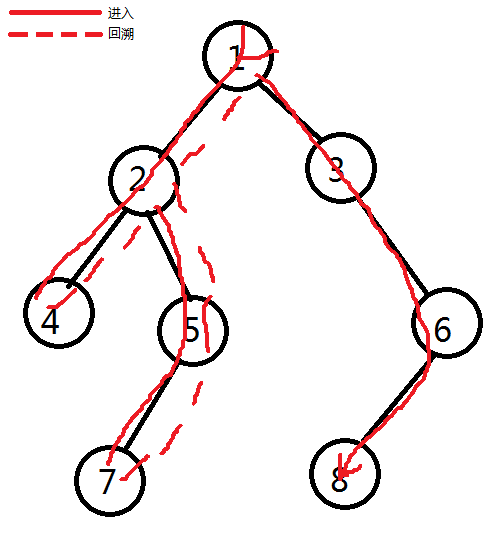从遍历树上来看，这两个算法似乎在代码上搭不着边，可是他们甚至可以用同一串代码！但在开始之前，我们需要来了解一些知识……

核心

基于队列的逐层枚举算法。
\(\hspace{2cm}\)——\(\sf\small\color{black}David\)\(\sf\small\color{EEEEEE}没错，又是他!\)

啥是 \(\sf\color{red}队列\) ？
那为啥要用队列？
先来回顾一下 DFS 。
DFS 每次找到一个可拓展状态时，就直接进了，无所顾忌。
可 BFS 就不一样了。他需要把整个层遍历完才可以遍历下一层。
怎么办呢？
\(唉，你先排着队，我先遍历这层的，等你排到了，我再来遍历你。\)
好的，现在，问题不小心解决了……
每一次处理队首，遍历到的新状态就让其入队，直到……
直到什么？
当找到了目标“顾客” \(\sf\small\color{gray}目标态\) ，或者“顾客”走光了\(\sf\small\color{gray}穷举\)，遍历就结束了。

加以运用

回家

小 H 在一个划分成了 n×m 个方格的长方形封锁线上。

• 每次他能向上下左右四个方向移动一格（当然小 H 不可以静止不动）， 但不能离开封锁线，否则就被打死了。
• 刚开始时他有满血 6 点，每移动一格他要消耗 1 点血量。
• 一旦小 H 的血量降到 0， 他将死去。
• 他可以沿路通过拾取鼠标（什么鬼。。。）来补满血量。
• 只要他走到有鼠标的格子，他不需要任何时间即可拾取。
• 格子上的鼠标可以瞬间补满，所以每次经过这个格子都有鼠标。
• 就算到了某个有鼠标的格子才死去， 他也不能通过拾取鼠标补满 HP。
• 即使在家门口死去， 他也不能算完成任务回到家中。
• 地图上有五种格子：
  0：障碍物。
  1：空地， 小 H 可以自由行走。
  2：小 H 出发点， 也是一片空地。
  3：小 H 的家。
  4：有鼠标在上面的空地。

小 H 能否安全回家？如果能， 最短需要多长时间呢？

如果是 BFS ，那么需要队列里的每一个元素都有四个属性： x 坐标， y 坐标， Hp 血量以及 Lv 层数/时间。
每一轮处理时，都取出队首的元素，向四个方向拓展。
此题特别注意判断顺序。
stl 的 queue<typename> 挺方便的。

初始化

声明队列、地图、元素结构体、转移数组、出图函数。此处声明Visit为int类型是为了避免被这样的数据hack掉。Visit里存路过这里时有过的最大血量。这样就可以保证每次来到这里时血量都是最优的，也就是说只要这里我之前来过，而且之前来的时候有着比现在更多的血量，那么我上次来比我这次来更优。注意此处是严格大于，否则可能会转起圈来。

#include<cstdio>
#include<queue>
using std::queue;
int Map[11][11],Visit[11][11],N,M,SX,SY,EX,EY;
const int D[4][2]={{1,0},{0,1},{-1,0},{0,-1}};
struct Point
{
	int x,y;
	int hp;
	int lv;
};
queue<Point> Search;
bool outmap(int x,int y){return (x<1||x>N||y<1||y>M);}

算法实现

初始元素、循环处理、拓展。
让该函数返回答案。
注意判断顺序。

int gohome()
{
	Search.push((Point){SX,SY,6,0});
	while(!Search.empty())
	{
		const Point S=Search.front();
		Search.pop();
		for(int i=0;i<4;i++)
		{
			Point N=(Point){S.x+D[i][0],S.y+D[i][1],S.hp-1,S.lv+1};
			if(outmap(N.x,N.y))		continue;
			if(N.hp<=0)				continue;
			if(Map[N.x][N.y]==0)	continue;
			if(Map[N.x][N.y]==3)	return N.lv;
			if(Map[N.x][N.y]==4)	N.hp=6;
			if(Visit[N.x][N.y]>=N.hp)continue;
			Visit[N.x][N.y]=N.hp;
			Search.push(N);
		}
	}
	return -1;
}

完整代码

#include<queue>
using std::queue;
int Map[11][11],Visit[11][11],N,M,SX,SY,EX,EY;
const int D[4][2]={{1,0},{0,1},{-1,0},{0,-1}};
struct Point
{
	int x,y;
	int hp;
	int lv;
};
queue<Point> Search;
bool outmap(int x,int y){return (x<1||x>N||y<1||y>M);}
void scanmap()
{
	for(int i=1;i<=N;i++)
		for(int j=1;j<=M;j++)
		{
			scanf("%d",&Map[i][j]);
			if(Map[i][j]==2)		SX=i,SY=j;
			else if(Map[i][j]==3)	EX=i,EY=j;
		}
}
int gohome()
{
	Search.push((Point){SX,SY,6,0});
	while(!Search.empty())
	{
		const Point S=Search.front();
		Search.pop();
		for(int i=0;i<4;i++)
		{
			Point N=(Point){S.x+D[i][0],S.y+D[i][1],S.hp-1,S.lv+1};
			if(outmap(N.x,N.y))		continue;
			if(N.hp<=0)				continue;
			if(Map[N.x][N.y]==0)	continue;
			if(Map[N.x][N.y]==3)	return N.lv;
			if(Map[N.x][N.y]==4)	N.hp=6;
			if(Visit[N.x][N.y]>=N.hp)continue;
			Visit[N.x][N.y]=N.hp;
			Search.push(N);
		}
	}
	return -1;
}
int main()
{
	scanf("%d%d",&N,&M);
	scanmap(); 
	printf("%d",gohome());
	return 0;
} 

说些别的……

为什么 DFS 和 BFS 都是搜索，可是代码却大相径庭，为什么呢？
其实 DFS 也可以这么写，只不过用的不是队列。
是 \(\sf\color{red}栈\) 。

算法优劣

BFS 主要优在时间。
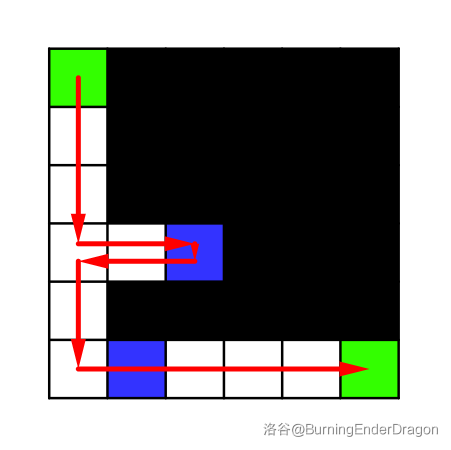
看看这张图， BFS 枚过的面积只是 DFS 的一半。
\(\sf\small\color{gray}BFS比DFS的图枚得快一些，所以不能看时间，要看枚过的面积。\)

BFS	DFS

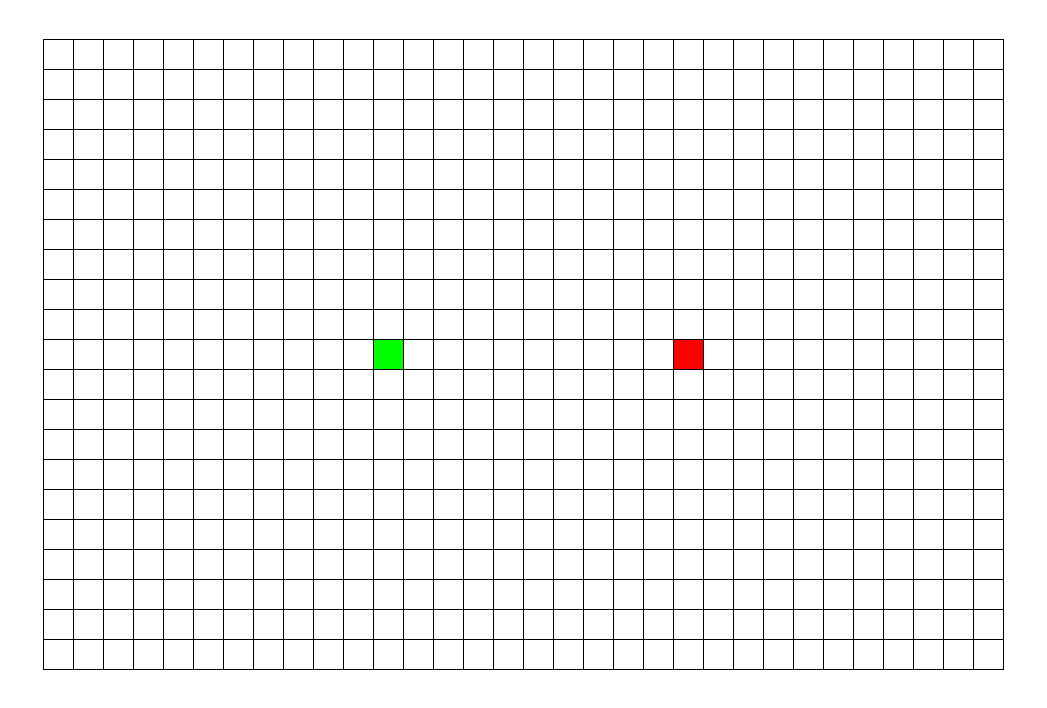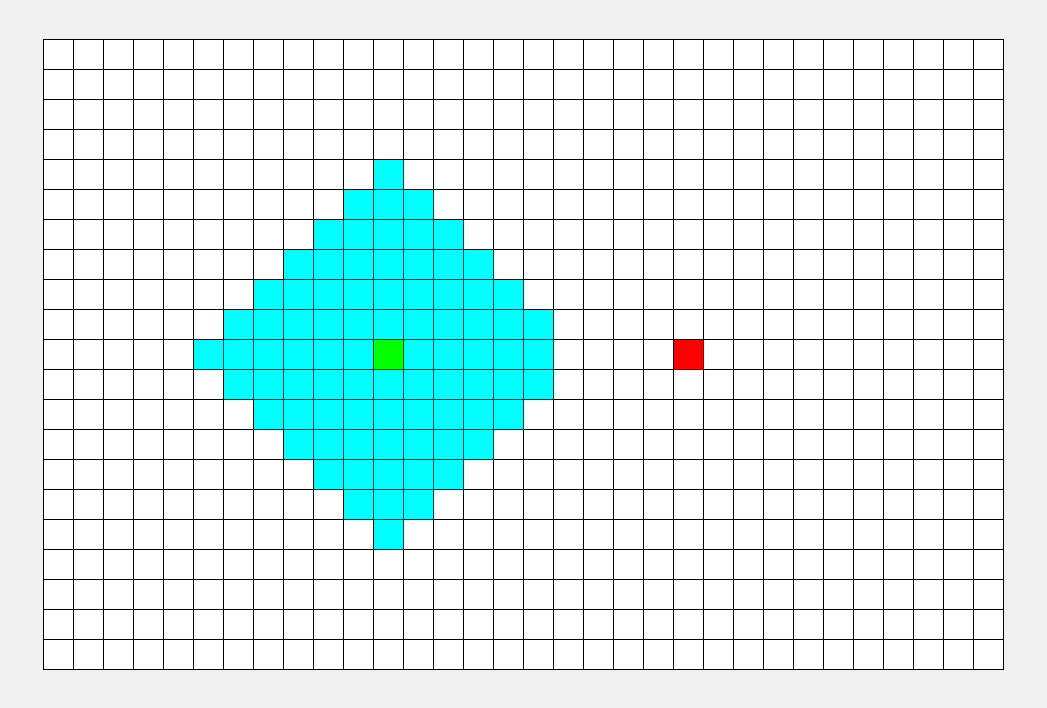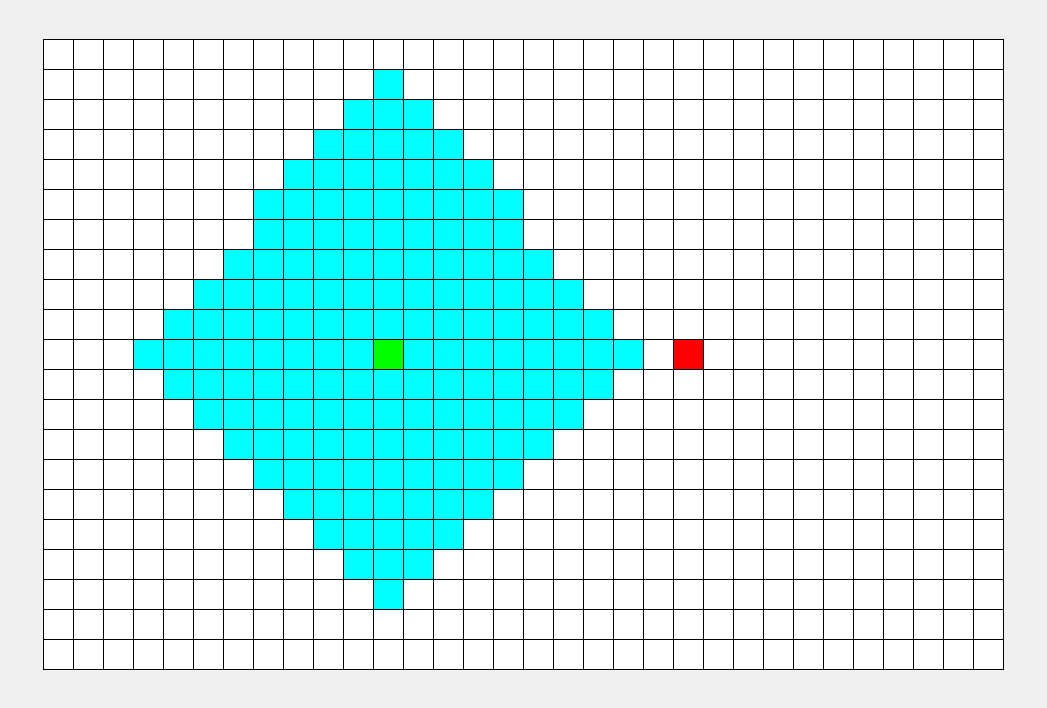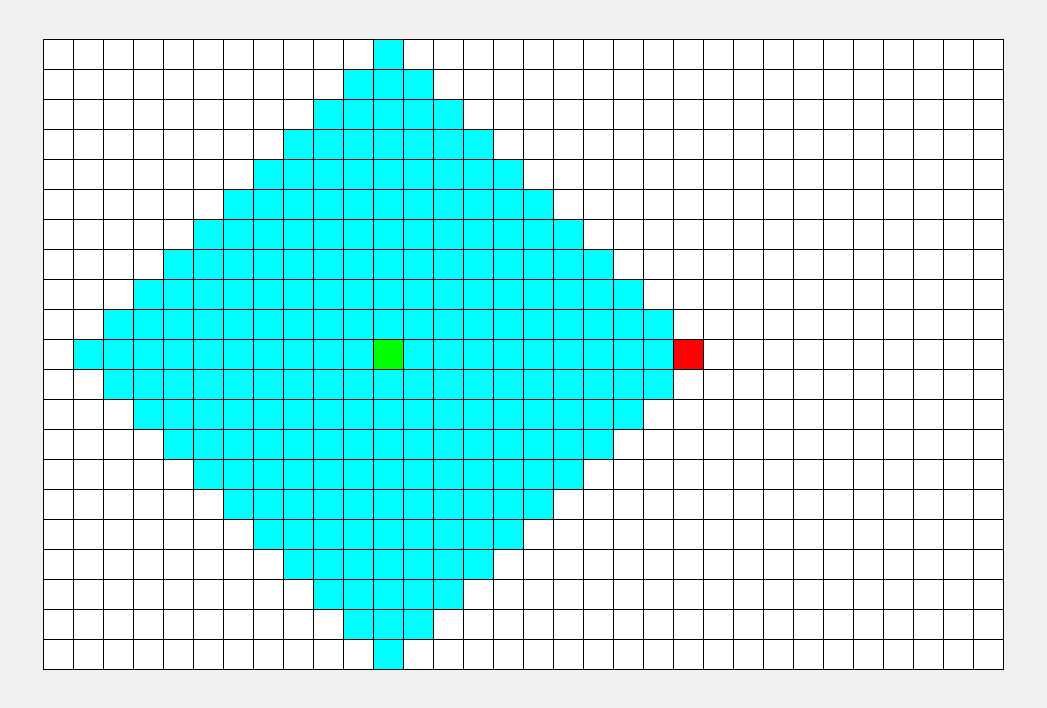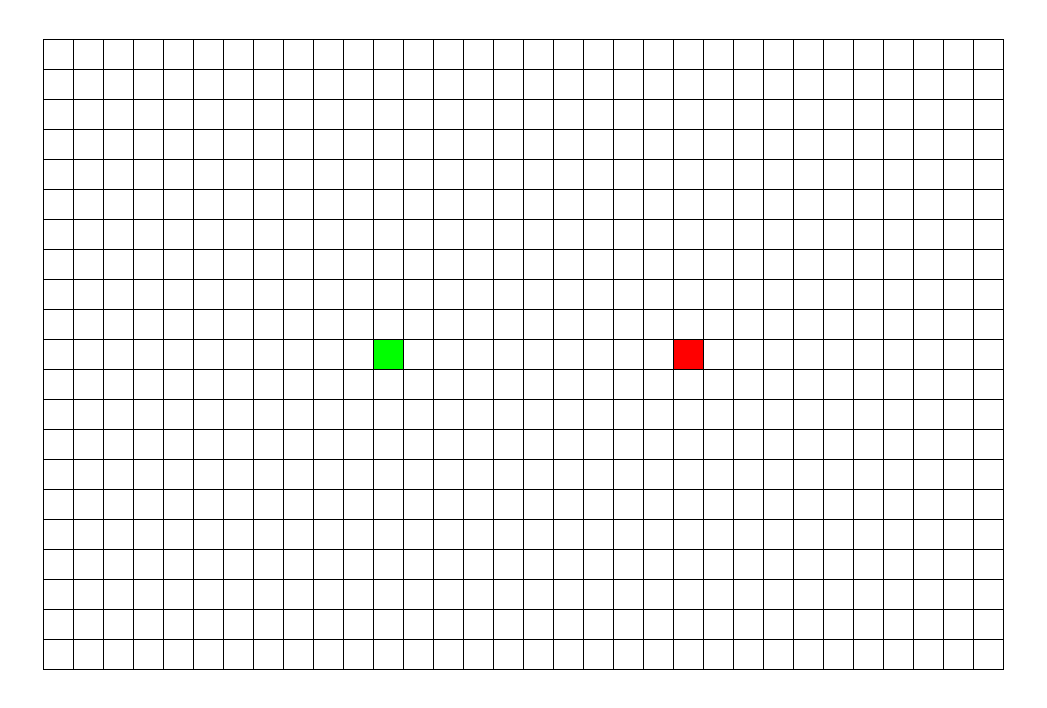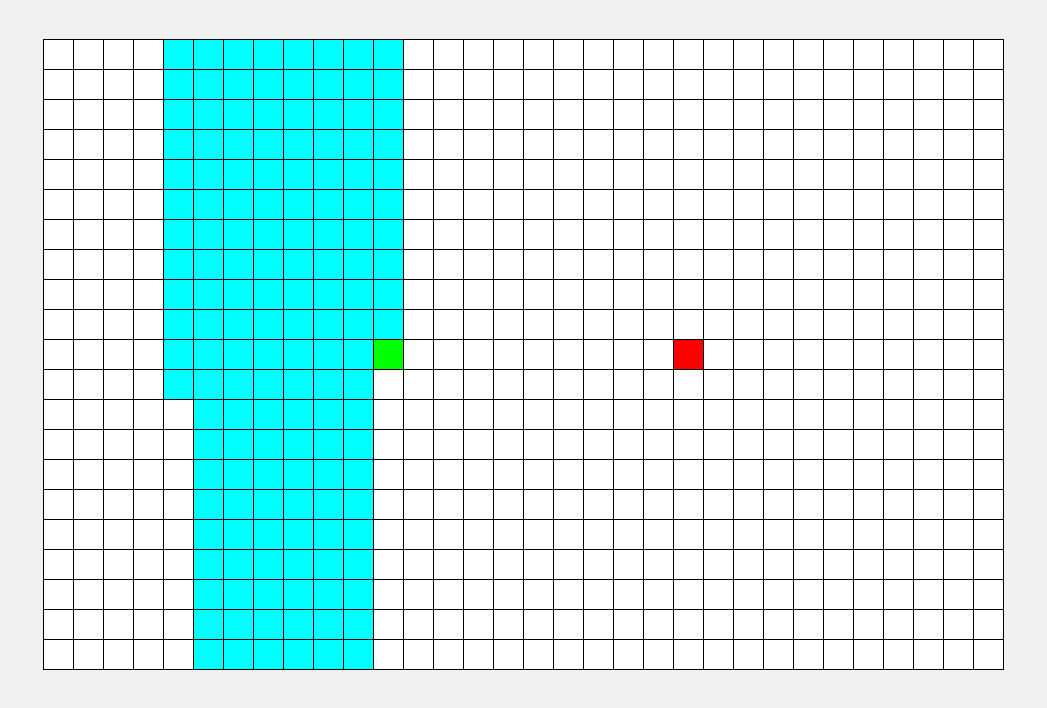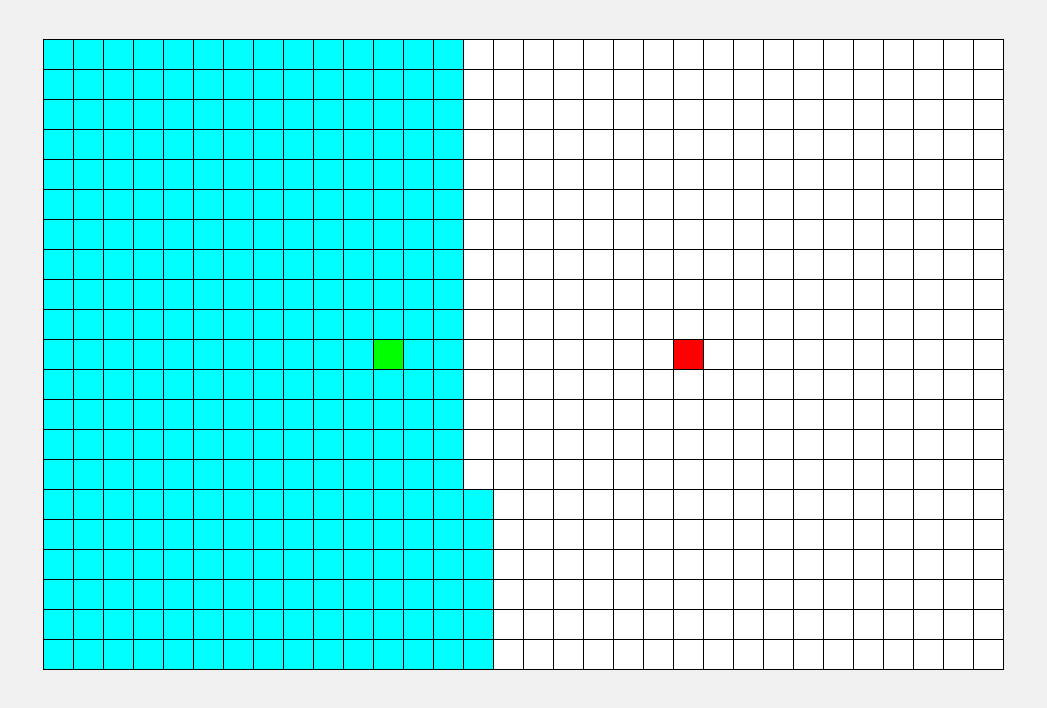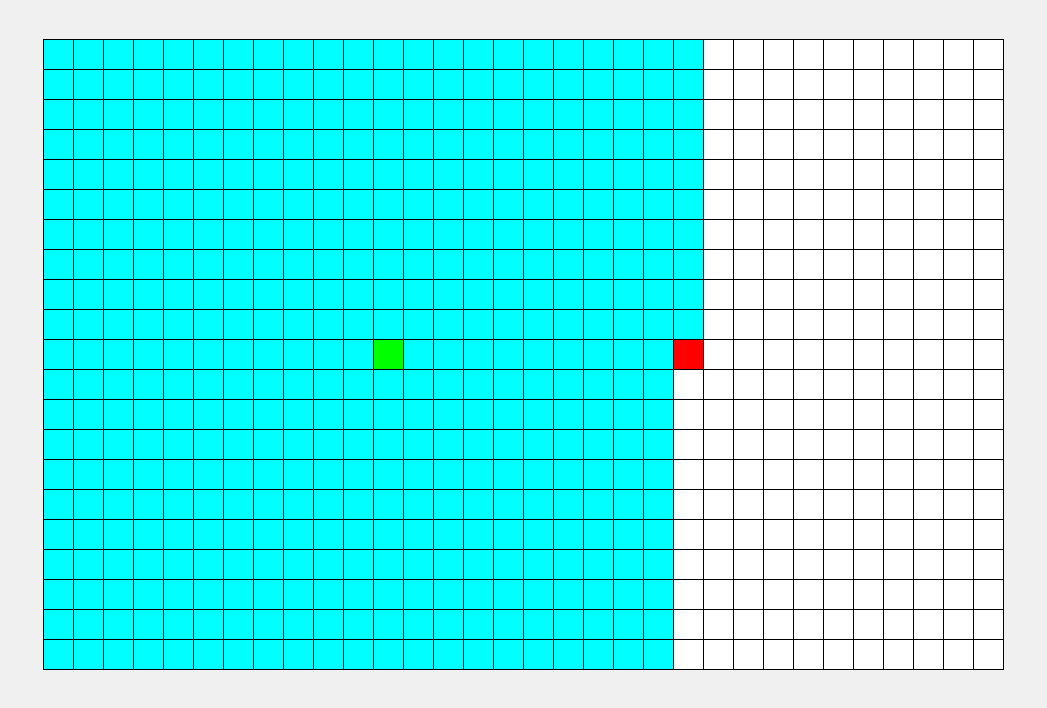可以看到， BFS 时间较平均，而 DFS 很大程度上取决于终点的位置。

---

_完结散花