LGP8476 [GLR R3] 惊蛰 学习笔记

LGP8476 [GLR R3] 惊蛰 学习笔记

Luogu Link

前言

纪念一下我在巨佬的大力帮助下过掉的高妙线段树优化 dp。

题意简述

给定非负整数序列 \(\{a_n\}\)，定义函数 \(w(x,y)\) 为

\[w(x,y)=\begin{cases} x-y,&x\ge y\\ C,&x< y \end{cases}, \]

其中 \(C\) 是给定常数。

你需要帮天依和绫请构造一个不增非负整数序列 \(\{b_n\}\)，最小化

\[\sum_{i=1}^n w(b_i,a_i) \]

你仅需输出这一最小化的结果。

做法解析

首先考虑最暴力的做法。\(O(nV^2)\) 的 dp 是这样的：设 \(dp_{i,j}\) 表示考虑到第 \(i\) 个人，\(b_i=j\) 时的最小代价，不难得出转移柿子：\(dp_{i,j}=\min_{k=j}^V dp_{i-1,k}+W(j,a_i)\)。

什么你问我这个题为什么是 \(\texttt{DP}\) ？分析无后效性子结构等等，长得还是很像线性 \(\texttt{DP}\) 的吧。

这个做法可以让我们获得一颗鸭蛋。不过有一个明显优化：每次取 \(\min\) 的过程其实是在取后缀最小值，所以加个后缀和优化，就能做到 \(O(nV)\) 并拿下 \(\text{15pts}\)。

这部分核心代码：

lolo calc(int a,int b){return (a<=b)?b-a:C;}
int main(){
    readis(N,C);memset(dp,0x3f,sizeof(dp));
    for(int i=1;i<=N;i++)readi(A[i]),maxxer(V,A[i]);
    sfx[V+1]=Inf;
    for(int i=V;i>=0;i--)dp[1][i]=calc(A[1],i),sfx[i]=min(sfx[i+1],dp[1][i]);
    for(int i=2;i<=N;i++){
        for(int j=0;j<=V;j++)dp[i][j]=sfx[j]+calc(A[i],j);
        for(int j=V;j>=0;j--)sfx[j]=min(sfx[j+1],dp[i][j]);
    }
    lolo ans=Inf;
    for(int i=0;i<=V;i++)minner(ans,dp[N][i]);
    writil(ans);
    return 0;
}

考虑正解，不难发现 \(w(j,a_i)\) 的转移暗藏着不少共性：要么加个常量，要么加个等差数列；这个巨佬的博客启示我们——

若某一维（通常是后一维）的转移具有较强的共性时，可以考虑利用整体 \(\texttt{DP}\) 优化。

分析到这一步，肯定不能不考虑线段树了。线段树优化线性 \(\texttt{DP}\) 的常用套路实际上是把原 \(\texttt{DP}\) 的第一维滚掉（因为转移都只与 \(dp_{i-1}\) 的值有关），然后把余下的一维数组摊到线段树上维护。

考虑一下我们在线段树上要干些什么。推一下可以发现：我们每一轮更新首先是在 \(sfx\) 数组上，以 \(a_i\) 为界，\([0,a_i)\) 上面我们区间加一个常量 \(C\)（对应原题中“老师会不高兴”这部分），\([a_i,N]\) 部分我们加一个首项为 \(0\)，公差为 \(1\) 的等差数列（对应原题中“选手会不高兴”这部分）。这个时候其实我们得到的就是整个 \(dp_i\) 数组；然后我们对它做一遍后缀和，以得到下次转移的基础。不妨画个图直观理解：

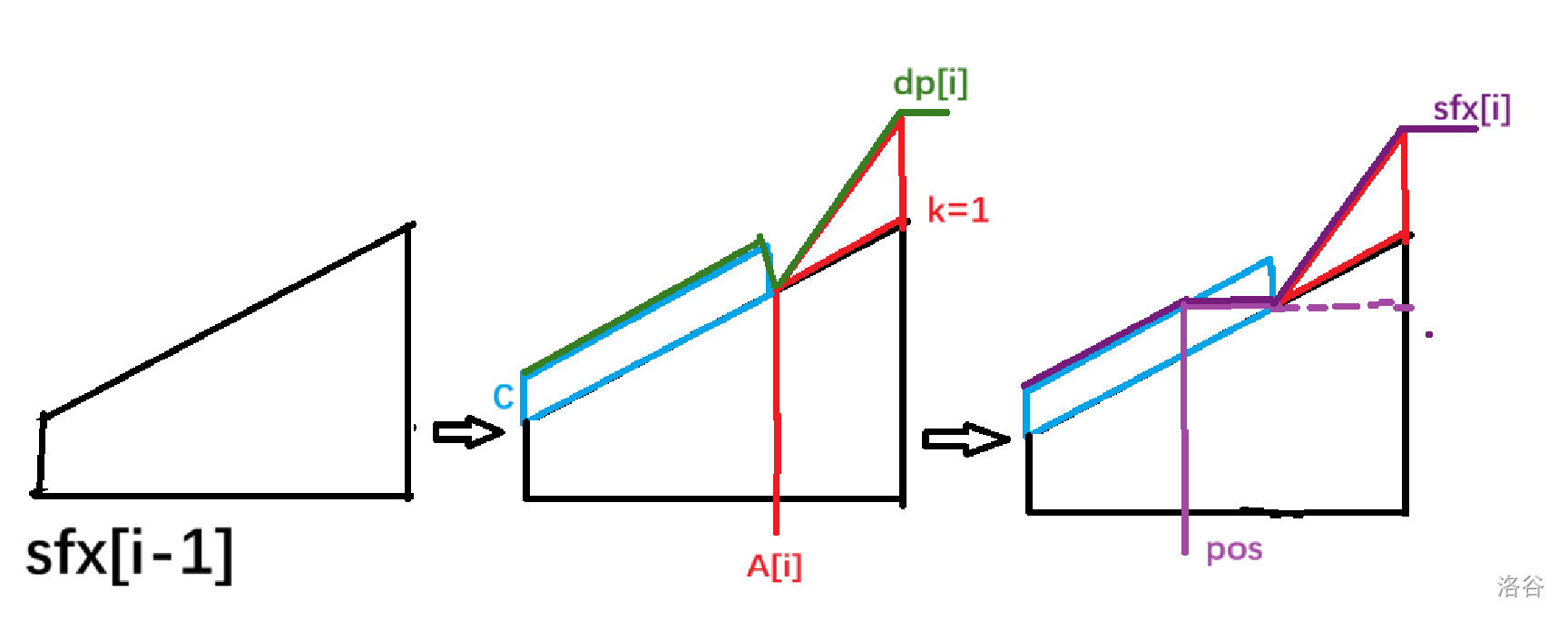
最后答案就是最后一轮更新完时的全局最小值。

线段树上，支持区间加，维护区间最小值都是平凡的；其它操作似乎都没有那么平凡；不过，我们要有一双善于发现单调性的眼睛！

现在你真的有一双发现单调性的眼睛吗？比如，\(\texttt{LGP12263}\)？

观察到 \(sfx\) 永远单调不降，\(dp\) 以 \(a_i\) 为界前后两段也永远单调不递减。

单调性既保证了支持等差数列加操作时也可以很正确地维护区间最小值（因为这题里面等差数列也是个单调不递减的东西，单调不递减+单调不递减=单调不递减，区间最小值一定在最左端）也保证了我们可以通过线段树上二分的方式找到左区间第一个大于等于 \(dp_{i,a_i}\) 值的位置（记为 \(pos\)），然后把 \([pos,A_i)\) 推平。

好了这题讲完了，接下来就是代码实现了！记得离散化（显然我们的 \(b_i\) 一定在取某个 \(a_i\) 时最优）！

代码实现

关于区间加等差数列操作，参考这↑里↓。

所以我们最后需要维护多少操作？维护最小值，支持区间加、区间等差数列加、线段树二分 \(i\) 左边第一个满足条件的下标、区间推平。

等差数列的公差固定为 \(1\)，所以不是很麻烦大概。

#include <bits/stdc++.h>
using namespace std;
using namespace obasic;
const int MaxN=1e6+5;
const lolo Inf=1e18;
int N,C,A[MaxN],B[MaxN],M;
struct SegTree{
    int cl[MaxN<<2],cr[MaxN<<2],cmid[MaxN<<2];lolo mn[MaxN<<2];
    lolo atag[MaxN<<2],dtag[MaxN<<2],ftag[MaxN<<2];
    int ls(int u){return u<<1;}
    int rs(int u){return (u<<1)|1;}
    void pushup(int u){mn[u]=min(mn[ls(u)],mn[rs(u)]);}
    void makeatag(int u,lolo x){mn[u]+=x,atag[u]+=x;}
    void makeftag(int u,lolo x){mn[u]=ftag[u]=x,atag[u]=dtag[u]=0;}
    void makedtag(int u,lolo x){mn[u]+=B[cl[u]]*x,dtag[u]+=x;}
    void pushdown(int u){
        if(ftag[u]!=-1)makeftag(ls(u),ftag[u]),makeftag(rs(u),ftag[u]),ftag[u]=-1;
        if(atag[u])makeatag(ls(u),atag[u]),makeatag(rs(u),atag[u]),atag[u]=0;
        if(dtag[u])makedtag(ls(u),dtag[u]),makedtag(rs(u),dtag[u]),dtag[u]=0;
    }
    void build(int u,int l,int r){
        cl[u]=l,cr[u]=r,ftag[u]=-1;if(l==r)return;
        int mid=(l+r)>>1;cmid[u]=mid;
        build(ls(u),l,mid),build(rs(u),mid+1,r);
        pushup(u);
    }
    void addupd(int u,int dl,int dr,lolo x){
        if(dl<=cl[u]&&cr[u]<=dr){makeatag(u,x);return;}
        pushdown(u);
        if(dl<=cmid[u])addupd(ls(u),dl,dr,x);
        if(dr>cmid[u])addupd(rs(u),dl,dr,x);
        pushup(u);
    }
    void flaupd(int u,int dl,int dr,lolo x){
        if(dl<=cl[u]&&cr[u]<=dr){makeftag(u,x);return;}
        pushdown(u);
        if(dl<=cmid[u])flaupd(ls(u),dl,dr,x);
        if(dr>cmid[u])flaupd(rs(u),dl,dr,x);
        pushup(u);
    }
    void arpupd(int u,int dl,int dr,lolo cd,lolo k){
        if(dl<=cl[u]&&cr[u]<=dr){makeatag(u,cd),makedtag(u,k);return;}
        pushdown(u);
        if(dl<=cmid[u])arpupd(ls(u),dl,dr,cd,k);
        if(dr>cmid[u])arpupd(rs(u),dl,dr,cd,k);
        pushup(u);
    }
    lolo getmin(int u,int dl,int dr){
        if(dl<=cl[u]&&cr[u]<=dr)return mn[u];
        pushdown(u);lolo res=Inf;
        if(dl<=cmid[u])minner(res,getmin(ls(u),dl,dr));
        if(dr>cmid[u])minner(res,getmin(rs(u),dl,dr));
        pushup(u);return res;
    }
    int lstser(int u,int dd,lolo x){
        if(cl[u]>dd||mn[u]>x)return 0;
        if(cl[u]==cr[u])return cl[u];
        pushdown(u);int cres=lstser(rs(u),dd,x);
        return cres?cres:lstser(ls(u),dd,x);
    }
}SgT;
int main(){
    readis(N,C);
    for(int i=1;i<=N;i++)readi(A[i]),B[i]=A[i];
    sort(B+1,B+N+1),M=unique(B+1,B+N+1)-(B+1),SgT.build(1,1,M);
    for(int i=1;i<=N;i++)A[i]=lwberi(B,M,A[i]);
    for(int i=1,pos;i<=N;i++){
        SgT.arpupd(1,A[i],M,-B[A[i]],1);
        if(A[i]==1)continue;
        SgT.addupd(1,1,A[i]-1,C);
        lolo val=SgT.getmin(1,A[i],A[i]);
        pos=SgT.lstser(1,A[i]-1,val);
        if(pos<A[i]-1)SgT.flaupd(1,pos+1,A[i]-1,val);
    }
    writil(SgT.mn[1]);
    return 0;
}