动态规划——516. 最长回文子序列

动态规划——516. 最长回文子序列

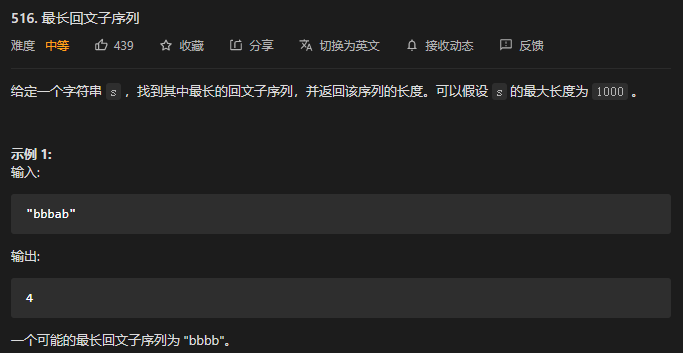
题目：

思路：

1. dp数组的定义：dp[i] [j]代表在字串s [i , ... , j ] 中，最长回文子序列的长度。

2. base_case：dp[i] [i] = 1

3. 状态转移方程：

   if (s[i] == s[j])
       // 它俩一定在最长回文子序列中
       dp[i][j] = dp[i + 1][j - 1] + 2;
   else
       // s[i+1..j] 和 s[i..j-1] 谁的回文子序列更长？
       dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
   

代码：

class Solution {
public:
    int longestPalindromeSubseq(string s) {
        int n = s.size();
        int dp[n][n];
        memset(dp, 0, sizeof(dp));
        for(int i=0; i<n; i++){
            dp[i][i] = 1;
        }
        for(int i = n-1;i>=0;i--){
            for(int j =i+1; j<n;j++){
                if(s[i] == s[j]){
                    dp[i][j] = dp[i+1][j-1] + 2;
                }else{
                    dp[i][j] = max(dp[i+1][j], dp[i][j-1]);
                }
            }
        }
        return dp[0][n-1];
    }
};

Rank：

Tips：