Programming Pearls笔记之二

Programming Pearls笔记之二

Programming Pearls笔记之二

　　这里是编程珠玑（Programming Pearls）第二部分（中间五个专栏）的笔记．

1 效率和正确性

  • 问题 
    有句话说＂效率是第二位的，结果是第一位的－－如果结果都错了，再快又有何用＂．这种观点正确吗？
  • 解答

    　　当错误不是太严重以至于影响结果的时候时间更重要．比如对于一些大型系统，与其修改１０个ｂｕｇ，人们往往更愿意将速度提高１０倍．

2 最大子序列和

  • 问题

    　　这是一道ＯＪ题目，没想到在这里见到了它．或许这就是这个题目的出处？ 

    对于一组整数，求连续最大子序列和．
  • Ｏ（ｎ＾２）解法

    　　这种时间复杂的算法很好设计．这里给出一个比较有启发性的． 

    cumarr[-1]=0
for i = [0, n)
    cumarr[i] = cumarr[i-1] + x[i]
maxsofar = 0
for i = [0, n)
    for j = [i, n)
        sum = cumarr[j] - cumarr[i-1]
        /* sum is sum of x[i..j] */
        maxsofar = max(maxsofar, sum)

    　　这里用到了累加求和，很有用处（比如下面的问题 累加数组 就能用到）．但这里的求和很盲目，对所有的都求，因此并没有能降低时间复杂度．我们知道如果ｘ［ｉ．．ｊ］是最大子序列和，这就说明对于任意的ｋ（ｉ≤ｋ≤ｊ），ｓｕｍ［ｉ．．ｋ］≥０．否则ｓｕｍ［ｋ＋１．．ｊ］将是最大的子序列．因此我们在求和的时候可以每遇到ｃｕｍａｒｒ［ｉ－１］为负时，就不再让ｃｕｍａｒｒ［ｉ］　＝　ｃｕｍａｒｒ［ｉ－１］　＋　ｘ［ｉ］，而让ｃｕｍａｒｒ［ｉ］　＝　０．这时时间复杂度就可以降至Ｏ（ｎ）．

  • Ｏ（ｎ）解法

    　　根据上面的思路，解法如下． 

    cumarr[-1] = 0
maxsofa = 0
for i = [0, n]
    cumarr[i] = max(cumarr[i-1], 0)
    maxsofar = max(maxsofar, cumarr[0])

    　　下面是书上给出的一个利用动态归化来推导这个算法的过程．

    http://images.cnblogs.com/cnblogs_com/Open_Source/201208/201208050947148272.png

    图一　示意图

　　ｍａｘｅｎｄｉｎｇｈｅｒｅ是以当前下标为最后一个元素的最大子序列和（只有当包含当前元素值为０时可以是空序列），ｍａｘｓｏｆａｒ是从数组开始到当前下标为止的最大子序列和．假设对于当前下标ｉ－１成立．下面将这个状态推广到ｉ．对于ｉ，这时最大子序列和只有两种可能．要么还是ｍａｘｓｏｆａｒ，要么是ｍａｘｅｎｄｉｎｇｈｅｒｅ＋ｘ［ｉ］． ｍａｘｅｎｄｉｎｇｈｅｒｅ＋［ｉ］若小于０，则从０开始，于是代码如下． 

maxsofar = 0
maxendinghere = 0
for i = [0, n]
    /* invariant: maxendinghere and maxsofar
       are accurate for x[0..i-1] */
    maxendinghere = max(maxendinghere + x[i], 0)
    maxsofar = max(max, maxendinghere)

　　其实这和上面的伪代码基本是一样的．

  • Ｏ（ｎ　ｌｏｇ　ｎ）解法

    　　这是一个分治算法，虽然不是最优解，但可以锻炼下思维．直接给出算法． 

    float maxsum3(l, u)
    if (l > u)  /* zero elements */
        return 0
    if (l == u)  /* one elements */
        return max(0, x[l])

    m = (l + u) / 2
    /* find max crossing to left */
    lmax = sum = 0
    for (i = m; i >= l; i--)
        sum += x[i]
        lmax - max(lmax, sum)
    /* find max crossing to right */
    rmax = sum = 0
    for i = (m, u]
        sum += x[i]
        rmax = max(rmax, sum)
    return max(lmax+rmax, maxsum3(l, m), maxsum3(m+1, u))

3 累加数组

  • 问题 
    数组ｘ［０．．ｎ－１］中的元素初始化为０，经过ｎ步下面的操作，给出最终的数组元素．其中ｌ，ｕ和ｖ是每个操作的参数（０≤ｌ≤ｕ<ｎ，是整数；ｖ是实数）．
for i = [l, u]                    ①
    x[i] += v                     ②
  • 解答

    　　这个问题用累加数组来解决．操作①、②对应于ｃｕｍ［ｌ］＋＝ｖ；ｃｕｍ［ｕ＋１］－＝ｖ．意思是让ｘ［ｌ．．ｎ－１］＋＝ｖ，然后再让ｘ［ｕ＋１．．ｎ－１］－＝ｖ．最终计算ｘ的方式是： 

    for (i = 0; i < n; i++)
  x[i] = x[i-1] + cum[i];

    　　书中给出的答案是让操作①、②对应于ｃｕｍ［ｕ］＋＝ｖ；ｃｕｍ［ｌ－１］－＝ｖ．最后计算ｘ时从后往前累加计算．

4 哨兵元素

  • 问题 
    利用哨兵元素求数组最大值．
  • 解答

    　　没什么知识可以学习，就觉得Ｒ．Ｇ．Ｄｒｏｍｅｙ这个解答有点儿耐人寻味． 

    i = 0
while i < n
    max = x[i]
    x[n] = max
    i++
    while x[i] < max
        i++

5 多项式计算

  • 问题 
    对于下面的多项式，优化下面的算法．
 y = a[0]
 xi = 1
 for i = [1, n]
     xi = x * xi
     y = y + a[i]*xi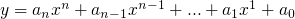

    $y = a_nx^n + a_{n-1}x^{n-1} + ... + a_1 x^1 + a_0$

  • 解答

    　　下面Ｈｏｒｎｅｒ的方法几乎可以使效率提高一倍． 

    y = a[n]
  for (i = n-1; i >= 0; i--)
    y = x*y + a[i]

Date: 2012-07-25 三

Author: Hu Wenbiao

Org version 7.8.11 with Emacs version 24

Validate XHTML 1.0
posted @ 2012-08-05 09:43  open source  阅读(390)  评论(0)  编辑  收藏  举报