深圳大学的一些简单题
A

打表,发现是这样的东西:
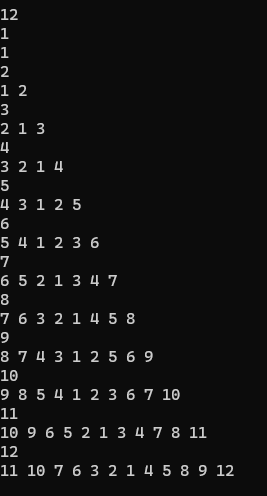
然后规律很显然,相邻的两个数,一组在左边,另一组在右边,依次循环,偶数的时候是 \(23\) 开头,奇数的时候是 \(12\) 开头,再处理一下 \(1\) 和 \(n\) 就可以,比较简单的分讨
显然规律不止一个
点击查看代码
#include <bits/stdc++.h>
using namespace std;
int a[1000001];
int main()
{
int t;
cin >> t;
while(t--)
{
int n;
cin >> n;
if(n == 1)
{
cout << 1 << endl;
continue;
}
else if(n == 2)
{
cout << "1 2" << endl;
continue;
}
if(n % 2 == 1)
{
int mid = (n + 1) / 2;
a[1] = n - 1;
a[n] = n;
a[mid] = 1;
for(int i = 2; i < mid; i++)
{
if(i % 2 == 0)
a[i] = a[i - 1] - 1;
else
a[i] = a[i - 1] - 3;
}
for(int i = n - 1; i > mid; i--)
{
if(i % 2 == 0)
a[i] = a[i + 1] - 3;
else
a[i] = a[i + 1] - 1;
}
}
else
{
int mid;
if(n % 4 == 0)
mid = n / 2 + 1;
else
mid = n / 2;
a[1] = n - 1;
a[n] = n;
a[mid] = 1;
for(int i = 2; i < mid; i++)
{
if(i % 2 == 0)
a[i] = a[i - 1] - 1;
else
a[i] = a[i - 1] - 3;
}
for(int i = n - 1; i > mid; i--)
{
if(i % 2 == 1)
a[i] = a[i + 1] - 3;
else
a[i] = a[i + 1] - 1;
}
}
for(int i = 1; i <= n; i++)
cout<<a[i]<<' ';
cout<<endl;
}
}
官解:

B


比较典的线段树,题目核心是找最小缺失编号、加/减球、移除最少的球使 \(x\) 是偶数,你可以用两个线段树
-
一个主线段树(ST_all),作用:维护编号 \(1\) 到 \(n\) 处的球数,支持区间更新,查询最小缺失编号 \(x\)
-
偶数编号线段树(st_even):只储存偶数编号的球数,和找到最少需要移除的球数,使得缺失的编号为偶数
具体实现:用 ST_all 来二分查询出第一个个数为 \(0\) 的下标 \(j\),没有的话就令 \(j = n+1\);用 ST_even 维护偶数位置,对于一个偶数 \(i\),如果球数是 \(b_i\),那么如果使用魔法取出所有 \(i\) 号球,其代价为 \(b_i\),更新时,由于更新是按原下标区间给出的,我们只对落在 \([l,r]\) 中且下标为偶数的数字进行更新。
判断胜负与代价时,假设现在缺的是 \(j\):
-
\(j\) 是偶数,那么 \(Thephix\) 已经赢了,就是 \(0\)
-
\(j\) 是奇数,让缺失数字变为 \(i\),需要代价是 \(b_i\),显然取成本最低的那个就行,如果区间 \([2,j-1]\) 内没有偶数,就不能获胜,输出 \(-1\),注意如果一开始 \(b_1 = 0\),或第一个缺失数字 \(j=1\),那么无论如何都赢不了,输出 \(-1\)
因为魔法移除只对当前回合起作用,回合结束后恢复原状态,因此我们只在查询时“虚拟地”考虑移除操作,不修改主数据结构
复杂度 \(O(m \log n)\)
点击查看代码
#include <iostream>
#include <vector>
#include <algorithm>
#include <cassert>
using namespace std;
typedef long long ll;
const ll INF = 1LL << 60;
int a[500001];
// 构造偶数下标数组(下标从1开始)
vector<int> even_idx;
vector<ll> even_a;
// 线段树模板:支持区间加更新和区间最小值查询
struct ST
{
int n;
vector<ll> tree, lazy;
ST(int n) : n(n)
{
tree.assign(4 * n, INF);
lazy.assign(4 * n, 0);
}
void build(int idx, int l, int r)
{
if(l == r)
{
tree[idx] = a[l - 1];
return;
}
int mid = (l + r) / 2;
build(idx * 2, l, mid);
build(idx * 2 + 1, mid + 1, r);
tree[idx] = min(tree[idx * 2], tree[idx * 2 + 1]);
}
void push_down(int idx, int l, int r)
{
if(lazy[idx] != 0)
{
int mid = (l + r) / 2;
lazy[idx * 2] += lazy[idx];
lazy[idx * 2 + 1] += lazy[idx];
tree[idx * 2] += lazy[idx];
tree[idx * 2 + 1] += lazy[idx];
lazy[idx] = 0;
}
}
void update(int idx, int l, int r, int ql, int qr, ll val)
{
if(ql > r || qr < l)
return;
if(ql <= l && r <= qr)
{
tree[idx] += val;
lazy[idx] += val;
return;
}
push_down(idx, l, r);
int mid = (l + r) / 2;
update(idx * 2, l, mid, ql, qr, val);
update(idx * 2 + 1, mid + 1, r, ql, qr, val);
tree[idx] = min(tree[idx * 2], tree[idx * 2 + 1]);
}
ll queryMin(int idx, int l, int r, int ql, int qr)
{
if(ql > r || qr < l)
return INF;
if(ql <= l && r <= qr)
return tree[idx];
push_down(idx, l, r);
int mid = (l + r) / 2;
return min(queryMin(idx * 2, l, mid, ql, qr), queryMin(idx * 2 + 1, mid + 1, r, ql, qr));
}
// 返回区间[ql,qr]内,第一个值为0的下标,如果不存在返回 -1
int q_first0(int idx, int l, int r, int ql, int qr)
{
if(ql > r || qr < l)
return -1;
if(ql <= l && r <= qr)
{
if(tree[idx] > 0)
return -1; // 此区间没有0
// 否则往下找
if(l == r)
return l;
}
push_down(idx, l, r);
int mid = (l + r) / 2;
int res = q_first0(idx * 2, l, mid, ql, qr);
if(res != -1)
return res;
return q_first0(idx * 2 + 1, mid + 1, r, ql, qr);
}
};
// 辅助函数:在一个排好序的偶数下标数组 even_idx 中,给定原区间 [L, R],返回在偶数数组中的左右下标区间
pair<int, int> get(int L, int R)
{
int l = int(lower_bound(even_idx.begin(), even_idx.end(), L) - even_idx.begin());
int r = int(upper_bound(even_idx.begin(), even_idx.end(), R) - even_idx.begin()) - 1;
if(l > r)
return {-1, -1};
return {l, r};
}
struct ST_e
{
int n;
vector<ll> tree, lazy;
ST_e(int n) : n(n)
{
tree.assign(4 * n, INF);
lazy.assign(4 * n, 0);
}
void build(int idx, int l, int r)
{
if(l == r)
{
tree[idx] = even_a[l - 1];
return;
}
int mid = (l + r) / 2;
build(idx * 2, l, mid);
build(idx * 2 + 1, mid + 1, r);
tree[idx] = min(tree[idx * 2], tree[idx * 2 + 1]);
}
void push_down(int idx, int l, int r)
{
if(lazy[idx] != 0)
{
int mid = (l + r) / 2;
lazy[idx * 2] += lazy[idx];
lazy[idx * 2 + 1] += lazy[idx];
tree[idx * 2] += lazy[idx];
tree[idx * 2 + 1] += lazy[idx];
lazy[idx] = 0;
}
}
void update(int idx, int l, int r, int ql, int qr, ll val)
{
if(ql > r || qr < l)
return;
if(ql <= l && r <= qr)
{
tree[idx] += val;
lazy[idx] += val;
return;
}
push_down(idx, l, r);
int mid = (l + r) / 2;
update(idx * 2, l, mid, ql, qr, val);
update(idx * 2 + 1, mid + 1, r, ql, qr, val);
tree[idx] = min(tree[idx * 2], tree[idx * 2 + 1]);
}
ll queryMin(int idx, int l, int r, int ql, int qr)
{
if(ql > r || qr < l)
return INF;
if(ql <= l && r <= qr)
return tree[idx];
push_down(idx, l, r);
int mid = (l + r) / 2;
return min(queryMin(idx * 2, l, mid, ql, qr), queryMin(idx * 2 + 1, mid + 1, r, ql, qr));
}
};
int n,m;
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, m;
cin >> n >> m;
for(int i = 0; i < n; i++)
cin >> a[i];
// 建立两个线段树
ST ST_all(n);
ST_all.build(1, 1, n);
for(int i = 1; i <= n; i++)
{
if(i % 2 == 0)
{
even_idx.push_back(i);
even_a.push_back(a[i - 1]);
}
}
int e_cnt = even_idx.size();
ST_e ST_even(e_cnt);
if(e_cnt > 0)
ST_even.build(1, 1, e_cnt);
// 每回合操作
// 注意:每回合更新都是对当前状态累积的
while(m--)
{
int l, r;
ll k;
cin >> l >> r >> k;
// 更新主线段树
ST_all.update(1, 1, n, l, r, k);
// 更新偶数下标树:更新所有偶数 i in [l, r]
if(e_cnt > 0)
{
// 在 even_idx 中寻找落在 [l, r] 的下标位置
auto pr = get(l, r);
if(pr.first != -1)
{
ST_even.update(1, 1, e_cnt, pr.first + 1, pr.second + 1, k);
}
}
// 查询第一个值为0的下标
int first0 = ST_all.q_first0(1, 1, n, 1, n);
int j; // j为自然状态下箱子中最小缺失数字,下标从1开始,如果都非0,则 j = n+1
if(first0 == -1)
{
j = n + 1;
}
else
{
j = first0;
}
// 如果 j == 1,则必定 b1==0,无论如何都无法获得胜利
if(j == 1)
{
cout << -1 << endl;
continue;
}
// 自然状态下,缺失数字为 j
// 如果 j 为偶数,则 Thephix 获胜,代价为0
if(j % 2 == 0)
{
cout << 0 << endl;
continue;
}
// j 为奇数,则需要利用魔法取出某个偶数 i (< j) 的球,代价为 b_i
// 在区间[1, j-1]中偶数下标集合:实际上就是偶数在区间 [2, j-1]
if(j - 1 < 2)
{
// 区间中没有偶数
cout << -1 << endl;
continue;
}
// 在 even_idx 中查找属于 [2, j-1] 的下标
auto pr = get(2, j - 1);
if(pr.first == -1)
{
cout << -1 << endl;
continue;
}
ll ans = ST_even.queryMin(1, 1, e_cnt, pr.first + 1, pr.second + 1);
// ans 为区间中最小的球数,也即移除该偶数所需代价
cout << ans << endl;
}
cout << "\n";
return 0;
}
官解:

C



点击查看代码
#include <bits/stdc++.h>
using namespace std;
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n;
int t;
cin >> t;
long long k;
while(t--)
{
cin >> n >> k;
string s;
cin >> s;
if(k >= n)
{
cout << 0 << "\n";
continue;
}
int ans = 0;
for(int r = 0; r < k && r < n; r++)
{
map<int,int> mp;
int cnt = 0;
for(int i = r; i < n; i += k)
{
mp[s[i] - 'a']++;
cnt++;
}
int a = 0;
for(int j = 0; j < 26; j++)
{
a = max(a, mp[j]);
}
ans += (cnt - a);
}
cout << ans << "\n";
}
return 0;
}
D
不会
E
不会
F
G
不会
H

显然可以二分,然后模拟一下就可以了
点击查看代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
struct node
{
int a, b;
} a[1000001];
int n;
bool check(ll t, ll p)
{
ll ma = 0;
ll nw = 0;
for(int i = 1; i <= n; i++)
{
ll aa = a[i].a;
ll b = a[i].b;
if(b <= t)
{
nw += aa;
if(nw < 0)
{
nw = 0;
}
ma = max(ma, nw);
}
else
{
nw = 0;
}
if(ma >= p)
{
return true;
}
}
return ma >= p;
}
ll find(ll p)
{
ll l = 1;
ll r = 1e18;
ll res = -1;
while(l <= r)
{
ll mid = l + (r - l) / 2;
if(check(mid, p))
{
res = mid;
r = mid - 1;
}
else
{
l = mid + 1;
}
}
return res;
}
int main()
{
int T;
cin >> T;
while(T--)
{
ll p;
cin >> n >> p;
for(int i = 1; i <= n; ++i)
{
cin >> a[i].a >> a[i].b;
}
ll mi = find(p);
cout << mi << endl;
}
return 0;
}
官解:

I
不会
J

普通情况:如果至少有一个 \(a_i >1\),那么就是普通的 Nim 博宇,判断是否 \(nim=0\) 即可
所有堆都是 \(1\) 时:显然谁赢取决于 \(n\) 的奇偶性
点击查看代码
#include <bits/stdc++.h>
using namespace std;
int a[1000001];
int main()
{
ios::sync_with_stdio(0);
cin.tie(nullptr);
int t;
cin >> t;
while(t--)
{
int n;
cin >> n;
int nim = 0;
bool all1 = 1;
for(int i = 0; i < n; i++)
{
cin >> a[i];
nim ^= a[i];
if(a[i] != 1)
all1 = 0;
}
bool win = 0;
if(all1)
{
// 如果所有堆都是1,先手获胜当堆数为偶数
win = (n % 2 == 0);
}
else
{
// 否则按照正常nim(异或不为0则获胜)
win = (nim != 0);
}
cout << (!win ? "Jiuhui" : "Akie") << "\n";
}
return 0;
}
官解:

K
不会
L
不会
M
不会

记录 \(uni\) 表示 \(i\) 波次的土包面积,\(uni_0 = 0,uni_{1<<i}\) 是第 \(i\) 个土包的面积
对于某个序列(例如我们选定集合 \(S\) 作为某一部分),我们“选定一个基波次作为首项”,比如设为 \(i\),序列价值就可以写成
其中 \(A\) 是允许加入的波次集合,\(cur\) 是表示当前已经加入的允许波次(二进制位表示),那么当前的联合集合就是
然后接下来加入的波次 \(j\),新增面积是
他的贡献为 \(k_i\) 乘上这个增量,状压 DP 一下,枚举所有加入顺序,转移状态是:
其中 \(K = uni_{(1<<i)\cup cur \cup (i<<j)}-uni_{(1<<i) \cup cur}\)
根据题意,最后答案是 \(\max best(s)+best(T)\),\(best(S) = \max_{i\in S} k_i \times uni_{1<<i} + dp(0)\),就是 \(cur = 0\) 时
复杂度高得离谱,肯定过不了,考虑优化
这一部分的思路没写代码,让 ds 仿照赛时代码写了一个,比较方便理解
点击查看代码
#include <bits/stdc++.h>
using namespace std;
// ----------------------
// 数据结构与凸包工具
// ----------------------
struct Point
{
int x, y;
};
// 计算向量 OA 与 OB 的叉积 (O, A, B)
long long cross(const Point &O, const Point &A, const Point &B)
{
return (long long)(A.x - O.x) * (B.y - O.y) - (long long)(A.y - O.y) * (B.x - O.x);
}
// 用 Andrew算法计算凸包,并返回“叉积和的绝对值”(即2倍面积,保证为整数);若不足3个点则返回0
long long convexHullArea(vector<Point> pts)
{
int n = pts.size();
if(n < 3)
return 0;
sort(pts.begin(), pts.end(), [](const Point & a, const Point & b)
{
return a.x == b.x ? a.y < b.y : a.x < b.x;
});
vector<Point> lower, upper;
for(int i = 0; i < n; i++)
{
while(lower.size() >= 2 && cross(lower[lower.size() - 2], lower[lower.size() - 1], pts[i]) <= 0)
lower.pop_back();
lower.push_back(pts[i]);
}
for(int i = n - 1; i >= 0; i--)
{
while(upper.size() >= 2 && cross(upper[upper.size() - 2], upper[upper.size() - 1], pts[i]) <= 0)
upper.pop_back();
upper.push_back(pts[i]);
}
lower.pop_back();
upper.pop_back();
vector<Point> hull;
for(auto &p : lower)
hull.push_back(p);
for(auto &p : upper)
hull.push_back(p);
long long area = 0;
int sz = hull.size();
for(int i = 0; i < sz; i++)
{
int j = (i + 1) % sz;
area += (long long)hull[i].x * hull[j].y - (long long)hull[i].y * hull[j].x;
}
return llabs(area);
}
// ----------------------
// 全局变量与预处理
// ----------------------
int n;
vector<vector<Point>> waves; // waves[i]保存第 i 组点
vector<int> K; // 每组的权值
vector<long long> unionAreaCache; // 对任一全局波次子集mask, unionAreaCache[mask]为其联合凸包面积(叉积和的绝对值)
// 预先计算每个mask对应的联合凸包面积
// 定义:mask=0时unionArea=0;mask中各bit表示选用了哪些波次
void computeUnionArea()
{
int total = 1 << n;
unionAreaCache.assign(total, 0);
for(int mask = 1; mask < total; mask++)
{
vector<Point> pts;
for(int i = 0; i < n; i++)
{
if(mask & (1 << i))
{
for(auto &p : waves[i])
pts.push_back(p);
}
}
long long area = convexHullArea(pts);
unionAreaCache[mask] = area;
}
unionAreaCache[0] = 0;
}
// ----------------------
// DP求序列价值
// ----------------------
//
// 固定序列“首项”为波次 base(用全局索引表示),设允许添加的其他波次集合为A (A为全局mask,不含base)
// 状态 dp(base, cur, A) 表示:当前已添加的波次集合为cur(均是从A中取的),当前联合集合为 ( (1<<base) U cur ) ,
// 接下来可选 j ∈ A\cur,加入时新增面积 = unionArea[ (1<<base) U cur U (1<<j) ] - unionArea[ (1<<base) U cur ] ,
// 对应贡献为 K[j] 乘上该增量。
//
// dp(base, cur, A) = max_{j in A\cur} { K[j] * (Δ) + dp(base, cur∪{j}, A) },若A\cur为空则返回0。
// 为简化,每次调用时固定全局变量 g_base 与 g_allowed = A。
// 状态仅由cur决定。状态cur均为全局mask。
int g_base, g_allowed;
vector<long long> dpMemo; // 下标范围0..(1<<n)-1(但只用到属于g_allowed的子集)
long long dp_func(int cur)
{
if(dpMemo[cur] != -1)
return dpMemo[cur];
long long best = 0;
int rem = g_allowed & (~cur);
for(int j = 0; j < n; j++)
{
if(rem & (1 << j))
{
int nxt = cur | (1 << j);
int curUnion = cur | (1 << g_base); // 当前联合集合
int nxtUnion = nxt | (1 << g_base);
long long delta = unionAreaCache[nxtUnion] - unionAreaCache[curUnion];
long long candidate = (long long)K[j] * delta + dp_func(nxt);
best = max(best, candidate);
}
}
dpMemo[cur] = best;
return best;
}
// 对于给定的波次集合 S(全局mask),计算该部分最佳序列价值:
// best(S)= max_{i in S} { K[i]*unionAreaCache[1<<i] + dp_func(0) },其中dp的允许集合为 S\{i}.
long long bestForSet(int S)
{
if(S == 0)
return 0;
long long bestVal = 0;
for(int i = 0; i < n; i++)
{
if(S & (1 << i))
{
int allowed = S & ~(1 << i);
long long init = (long long)K[i] * unionAreaCache[1 << i];
g_base = i;
g_allowed = allowed;
dpMemo.assign(1 << n, -1);
long long add = dp_func(0);
bestVal = max(bestVal, init + add);
}
}
return bestVal;
}
// ----------------------
// 主函数
// ----------------------
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
waves.resize(n);
K.resize(n);
// 依次读入每组数据:先读 m 和 k,然后 m 个点
for(int i = 0; i < n; i++)
{
int m, k;
cin >> m >> k;
K[i] = k;
waves[i].resize(m);
for(int j = 0; j < m; j++)
{
cin >> waves[i][j].x >> waves[i][j].y;
}
}
// 预处理:预计算所有波次集合的联合凸包面积
computeUnionArea();
// 枚举把 {0,1,...,n-1} 分成两部分:S 与 T(T为 S的补集),计算 bestForSet(S)+bestForSet(T) 的最大值
int totalMask = (1 << n) - 1;
long long ans = 0;
for(int S = 0; S < (1 << n); S++)
{
int T = totalMask ^ S;
long long curVal = bestForSet(S) + bestForSet(T);
ans = max(ans, curVal);
}
cout << ans << "\n";
return 0;
}
智障 ds 写了一年,还人工纠错了一下,AI 还是不能代替人类()
你会发现有很多重复的东西,所以要优化
记 \(unih_i\) 表示集合 \(mask\) 所有点合并后的土包
对于每个 \(mask\),找到其中最低位的 \(1\)(就是新增的组 \(P_i\)),有
然后就预处理完了所有子集的联合土包和面积,直接查表就行
定义 \(f(mask)\) 表示子集 \(mask\) 按照最优顺序入队的最大价值,有
其中 \(S-i\) 就是 \(S\) 去掉 \(i\) 之后的集合,然后就做完了
点击查看代码
//板子来源:菜菜园子
//你可以dp,分割枚举
//然后t了
//然后你要减少计算,把一些重复的子集吃了
//还有一些更新时的奇技淫巧
#include <bits/stdc++.h>
using namespace std;
struct Point
{
int x, y;
};
// 叉积
long long cross(const Point &O, const Point &A, const Point &B)
{
return (long long)(A.x - O.x) * (B.y - O.y) - (long long)(A.y - O.y) * (B.x - O.x);
}
// Andrew 算法计算凸包,返回结果为逆时针顺序的凸包顶点(可能退化成一条线或单点,面积为0)
vector<Point> con(vector<Point>& pts)
{
int n = pts.size();
if(n <= 1)
return pts;
sort(pts.begin(), pts.end(), [](const Point & a, const Point & b)
{
return a.x == b.x ? a.y < b.y : a.x < b.x;
});
vector<Point> hull;
// 下半部分
for(int i = 0; i < n; i++)
{
while(hull.size() >= 2 && cross(hull[hull.size() - 2], hull[hull.size() - 1], pts[i]) <= 0)
hull.pop_back();
hull.push_back(pts[i]);
}
// 上半部分
for(int i = n - 2, t = hull.size() + 1; i >= 0; i--)
{
while(hull.size() >= t && cross(hull[hull.size() - 2], hull[hull.size() - 1], pts[i]) <= 0)
hull.pop_back();
hull.push_back(pts[i]);
}
hull.pop_back();
return hull;
}
// 合并两个凸包:直接合并两凸包所有点,再计算凸包(因为总点数较小)
vector<Point> merge(const vector<Point>& A, const vector<Point>& B)
{
vector<Point> pts;
pts.insert(pts.end(), A.begin(), A.end());
pts.insert(pts.end(), B.begin(), B.end());
if(pts.empty())
return pts;
return con(pts);
}
// 计算凸多边形面积的2倍(整数)
long long pol_area(const vector<Point>& poly)
{
long long area = 0;
int n = poly.size();
for(int i = 0; i < n; i++)
{
int j = (i + 1) % n;
area += (long long) poly[i].x * poly[j].y - (long long) poly[i].y * poly[j].x;
}
return abs(area);
}
// 全局变量
int n;
vector<vector<Point>> a; // 原始点集(每组)
vector<vector<Point>> aaa; // 每组的凸包(预处理后)
vector<int> K; // 权值
// 对于每个ii(非0),存储所有包含组的联合凸包以及对应的面积(2倍面积)
vector<vector<Point>> uni_h;
vector<long long> uni_s;
// 预处理:计算每个组的凸包
void init11()
{
aaa.resize(n);
for(int i = 0; i < n; i++)
{
vector<Point> pts = a[i];
aaa[i] = con(pts);
}
}
// 预处理:状态压缩DP计算所有子集的联合凸包及面积
void init()
{
int tott = 1 << n;
uni_h.assign(tott, vector<Point>());
uni_s.assign(tott, 0);
// 空集:面积为0
uni_s[0] = 0;
for(int ii = 1; ii < tott; ii++)
{
// 找最低位i
int i = __builtin_ctz(ii);
int prev = ii ^ (1 << i);
if(prev == 0)
{
uni_h[ii] = aaa[i];
}
else
{
uni_h[ii] = merge(uni_h[prev], aaa[i]);
}
uni_s[ii] = pol_area(uni_h[ii]);
}
}
// DP:对于子集ii,计算最优入队顺序的价值 F(ii)
// 状态转移:F(ii) = max_{i in ii} { F(ii without i) + K[i] * (uni_s[ii] - uni_s[ii without i]) }
vector<long long> dp;
long long computeDP(int tot)
{
dp.assign(tot, 0);
dp[0] = 0;
// 枚举ii,采用按ii递增顺序(保证子状态已算好)
for(int ii = 1; ii < tot; ii++)
{
long long maa = 0;
// 枚举 ii 中的每个 i
// 可以用位运算枚举
int sub = ii;
while(sub)
{
int i = __builtin_ctz(sub);
int KK = ii ^ (1 << i);
long long c = dp[KK] + (long long)K[i] * (uni_s[ii] - uni_s[KK]);
maa = max(maa, c);
sub &= (sub - 1);
}
dp[ii] = maa;
}
return dp[tot - 1];
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
a.resize(n);
K.resize(n);
for(int i = 0; i < n; i++)
{
int m, k;
cin >> m >> k;
K[i] = k;
a[i].resize(m);
for(int j = 0; j < m; j++)
{
cin >> a[i][j].x >> a[i][j].y;
}
}
init11();
init();
int tott = 1 << n;
vector<long long> F(tott, 0);
F[0] = 0;
for(int ii = 1; ii < tott; ii++)
{
long long maa = 0;
int sub = ii;
while(sub)
{
int i = __builtin_ctz(sub);
int KK = ii ^ (1 << i);
long long c = F[KK] + (long long)K[i] * (uni_s[ii] - uni_s[KK]);
maa = max(maa, c);
sub &= (sub - 1);
}
F[ii] = maa;
}
long long ans = 0;
for(int i = 0; i < tott; i++)
{
int c = (tott - 1) ^ i;
ans = max(ans, F[i] + F[c]);
}
cout << ans << endl;
return 0;
}
官解:

翻了翻提交记录发现我竟然是最优解???


 浙公网安备 33010602011771号
浙公网安备 33010602011771号