LeetCode刷题笔记-11.盛最多水的容器(container-with-most-water)

问题描述

给你n个非负整数a1，a2，...，an，每个数代表坐标中的一个点(i, ai)。在坐标内画n条垂直线，垂直线i的两个端点分别为(i, ai)和(i, 0) 。找出其中的两条线，使得它们与x轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器。

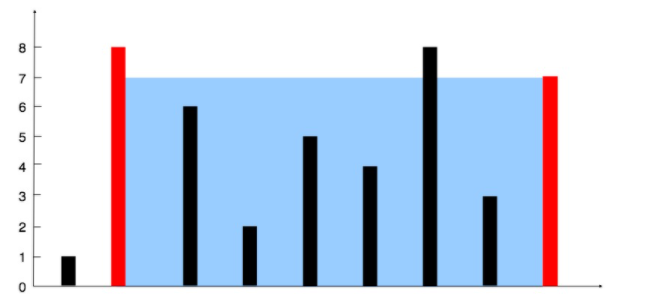
示例 1：

输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

示例 3：

输入：height = [4,3,2,1,4]
输出：16

示例 4：

输入：height = [1,2,1]
输出：2

提示：

• n = height.length
• 2 <= n <= 3 * 104
• 0 <= height[i] <= 3 * 104

题解

1.暴力解法

算法解析

该解法为最先想到解法,由于题目给予数据结构为数组,因此对每个组合遍历求出最大的值即可.此时共有\(C_n^2\)种组合.

复杂度分析

• 时间复杂度: \(O(N^2)\), 一共遍历\(C_n^2 = \frac{n(n-1)}{2}\)种组合
• 空间复杂度: \(O(1)\), 只需要固定的额外空间

代码实现

• Java版

class Solution {
    public int maxArea(int[] height) {
        int maxRes = 0;
        for (int i = 0; i < height.length; ++i) {
            for (int j = i+1; j < height.length; ++j) {
                int min = height[i] < height[j] ? height[i] : height[j];
                int tmpArea = (j-i)*min;
                if (tmpArea > maxRes) {
                    maxRes = tmpArea;
                }
            }
        }

        return maxRes;
    }
}

2.双指针解法

算法解析

该解法充分利用了题目所给的条件:

• 高度选取两边界中更小的一边.
• 宽度选取两元素的索引差的绝对值.

因此,使用一个左指针left指向数组开头,一个右指针right指向数组结尾.从两边向中间移动左右指针求出过程中的面积最大值.移动指针的规则如下:

• 当左指针指向元素(高度)更小时,移动左指针.
• 当右指针指向元素(高度)更小时,移动右指针.
  即移动左右边界,使宽度向中间收敛.并再此过程中找到最大面积.

双指针可以求解出正确结果的关键是舍去了遍历不必要的状态:
设每一状态下水槽面积为S(i, j), (0 <= i < j < n)

• 若不指定移动规则，所有移动出现的S(i, j)的状态数为\(C_n^2\)，即暴力枚举出所有状态。
• 在状态S(i, j)下向内移动短板至S(i + 1, j)（假设h[i] < h[j]），则相当于消去了{S(i, j-1), S(i, j-2), ... , S(i, i+1)}状态集合。而所有消去状态的面积一定 <= S(i, j)：
  • 短板高度：相比S(i, j)相同或更短（<= h[i]）；
  • 底边宽度：相比S(i, j)更短。

因此所有消去的状态的面积都 < S(i, j). 通俗的讲，我们每次向内移动短板，所有的消去状态都不会导致丢失面积最大值.

参考文章及资料

LeetCode官方题解
LeetCode精选题解

复杂度分析

• 时间复杂度: \(O(N)\), 双指针总计最多遍历整个数组一次
• 空间复杂度: \(O(1)\), 只需要固定的额外空间

代码实现

• Java版

class Solution {
    public int maxArea(int[] height) {
        int maxRes = 0, tmpArea;
        int l = 0, r = height.length-1;
        while (l < r) {
            tmpArea = (r-l)*(height[l] < height[r] ? height[l] : height[r]);
            maxRes = tmpArea > maxRes ? tmpArea : maxRes;
            if (height[l] < height[r]) {
                l++;
            } else {
                r--;
            }
        }

        return maxRes;
    }
}

• Python版

class Solution:
    def maxArea(self, height: List[int]) -> int:
        res = 0
        l, r = 0, len(height)-1
        while l < r:
            tmp_area = (r-l) * min(height[r], height[l])
            res = tmp_area if tmp_area > res else res
            if height[l] < height[r]:
                l += 1
            else:
                r -= 1
        return res

• C版

int maxArea(int* height, int heightSize)
{
    int resArea = 0, tmpArea;
    int l = 0, r = heightSize-1;
    while (l < r) 
    {
        tmpArea = (r-l) * (height[l] < height[r] ? height[l] : height[r]);
        resArea = tmpArea > resArea ? tmpArea : resArea;
        if (height[l] < height[r]) 
        {
            ++l;
        }
        else 
        {
            --r;
        }
    }

    return resArea;
}