10.18 %你赛总结
T1 一维围棋
思路
由于本人太蒟了,不会 \(O(n)\)。求教。
简单题目。首先,看到数据范围 \(|s| \le 100\),于是得到可以有 \(O(n^4)\) 做法。先 \(O(n)\) 枚举 \(s_i\) 对于是 . 的位置变成 W。然后 \(O(n^2)\) 枚举修改后的数组的每个子串,对于 \([l,r]\) 这个区间内的子串。当其满足 \(s_l\) 与 \(s_r\) 都为 W 且 \([l+1,r-1]\) 区间内全为 B 且 从 \(l-1\) 到 \(1\) 与 \(r+1\) 到 \(n\) 的字符第一个不是 W 的字符不为 B 即可。因为 \([l,r]\) 需要暴力 check。故总时间复杂度为 \(O(n^4)\)。可以通过此题。
AC code
#include<bits/stdc++.h>
#define int long long
using namespace std;
namespace WYL{
int n,ans;
string s,str;
int main(){
cin>>n;
cin>>s;
for(int i=0;i<s.size();i++){
str=s;
if(str[i]=='.'){
str[i]='W';
// cout<<str<<endl;
for(int l=0;l<s.size();l++){
for(int r=0;r<s.size();r++){
if(r-l+1<3){
continue;
}
int flag=0;
if(str[l]=='W'&&str[r]=='W'){
for(int j=l+1;j<=r-1;j++){
if(str[j]!='B'){
flag=1;
break;
}
}
}else{
continue;
}
// cout<<flag<<" ";
if(flag==1){
continue;
}
for(int j=l;j>=0;j--){
if(str[j]=='.'){
flag=0;
break;
}
if(str[j]=='B'){
flag=1;
break;
}
}
if(flag==1){
continue;
}
for(int j=r;j<=s.size()-1;j++){
if(str[j]=='.'){
flag=0;
break;
}
if(str[j]=='B'){
flag=1;
break;
}
}
if(flag==1){
continue;
}
ans=max(ans,r-l-1);
// cout<<l<<" "<<r<<endl;
}
}
}
}
cout<<ans<<endl;
return 0;
}
}
signed main(){
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
// freopen("capture.in","r",stdin);
// freopen("capture.out","w",stdout);
WYL::main();
return 0;
}
T2 斜二等轴测图
思路
其实跟 一元二次方程 难度差不多。这一提供两种思路。
第一。我们考虑把原图分成三个部分来看。我画个图,这就很明显了。
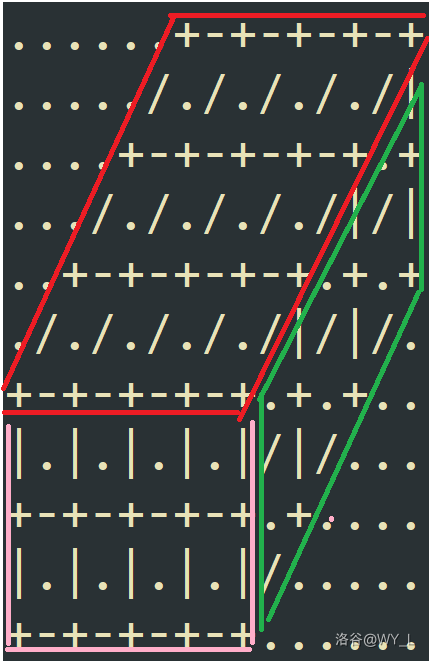
这个图是 \(a=4,b=3,c=2\) 的。我们对于每一行每一列进行奇偶判断在直接输出一下就可以了。这里提醒 数组要开大一点,不然怎么挂的你都不知道。
第二种思路也很一眼。这是我亲爱的同机房大佬提出的。我们可以把原图分层,分开处理 /,+ 和 -。这样没有上面那种解法容易挂分。但是我考场写的上面那种思路。于是顺其自然只提供思路一的代码(乐。
AC code
#include<bits/stdc++.h>
using namespace std;
namespace WYL{
int T,a,b,c,chang,kuan;
char mp[200][200];
void debug(){
for(int i=1;i<=kuan;i++){
for(int j=1;j<=chang;j++){
cout<<mp[i][j];
}
cout<<endl;
}
}
void shang(){
for(int i=1;i<=b*2+1;i++){
if(i%2==1){
int shuliang=a*2+1;
// cout<<shuliang<<endl;
int qianmiankong=chang-shuliang-i+1;
int sum=1;
for(int j=qianmiankong+1;j<=qianmiankong+shuliang;j++){
if(sum%2==1){
mp[i][j]='+';
}else{
mp[i][j]='-';
}
sum++;
}
}else{
int shuliang=a*2+1;
int qianmiankong=chang-shuliang-i+1;
int sum=1;
for(int j=qianmiankong+1;j<=qianmiankong+shuliang;j++){
if(sum%2==1){
mp[i][j]='/';
}else{
mp[i][j]='.';
}
sum++;
}
}
}
return;
}
void qian(){
int huangshu=c*2,sum=1;
for(int i=kuan;i>=kuan-huangshu+1;i--){
int shuliang=2*a+1;
if(sum%2==1){
int num=1;
for(int j=1;j<=shuliang;j++){
if(num%2==1){
mp[i][j]='+';
}else{
mp[i][j]='-';
}
num++;
}
}else{
int num=1;
for(int j=1;j<=shuliang;j++){
if(num%2==1){
mp[i][j]='|';
}else{
mp[i][j]='.';
}
num++;
}
}
sum++;
}
return;
}
void ce(){
int lieshu=b*2,sum=1,kaishi=2;
for(int i=chang;i>=chang-lieshu+1;i--){
if(sum%2==1){
int num=1;
for(int j=1;j<=2*c;j++){
if(num%2==1){
mp[j+kaishi-1][i]='|';
}else{
mp[j+kaishi-1][i]='+';
}
num++;
}
}else{
int num=1;
for(int j=1;j<=2*c;j++){
if(num%2==1){
mp[j+kaishi-1][i]='.';
}else{
mp[j+kaishi-1][i]='/';
}
num++;
}
}
sum++;
kaishi++;
}
return;
}
int main(){
cin>>T;
while(T--){
cin>>a>>b>>c;
chang=(a+b)*2+1;
kuan=(c+b)*2+1;
// cout<<chang<<" "<<kuan<<endl;
for(int i=1;i<=kuan;i++){
for(int j=1;j<=chang;j++){
mp[i][j]='.';
}
}
shang();
// debug();
qian();
// debug();
ce();
debug();
}
return 0;
}
}
int main(){
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
// freopen("draw.in","r",stdin);
// freopen("draw.out","w",stdout);
WYL::main();
return 0;
}
/*
1
4 3 2
2
1 1 1
6 2 4
*/
T3 [SNOI2017] 炸弹
思路
首先观察数据 $1 \le n \le 500000 $。得出如果暴力建图一定会超时。所以考虑线段树优化建图。用什么建图。这个很容易。就是把当前炸弹的坐标与它能够炸到区间连边。这个其实和 CF786B 差不多。但是,与这题不同的一个点其实也很明显。这个题目是有向图。所以在连好边之后我们考虑 tarjan 缩点将它变成 DAG。这样子就很好处理了。
得到这个 DAG 之后选择维护一个炸弹所能影响到的左边界和右边界。其实就是:
于是我们尝试反向建边再加一个拓扑排序就可以解决了。这里注意,缩完点之后不一定是一棵树,因为是有向图缩点捏。
AC code
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
namespace WYL{
const int N=8e6+10;
const int mod=1e9+7;
int n,head[N],to[N],cnt,nxt[N],tot,fa[N],num,id[N],p[N],r[N],times,dfn[N],low[N],Stack[N],top,opt[N],minn[N],maxn[N],indegree[N],q[N];
bool flag[N];
vector<int> edge[N];
void add(int u,int v){
to[++tot]=v;nxt[tot]=head[u];head[u]=tot;fa[tot]=u;
return;
}
void debug(){
for(int i=1;i<=n;i++){
cout<<opt[i]<<" ";
}
cout<<endl;
return;
}
void tarjan(int x){
dfn[x]=low[x]=++times;
Stack[++top]=x;
flag[x]=true;
for(int i=head[x];i;i=nxt[i]){
if(!dfn[to[i]]){
tarjan(to[i]);
low[x]=min(low[x],low[to[i]]);
}else if(flag[to[i]]){
low[x]=min(low[x],dfn[to[i]]);
}
}
int find;
if(low[x]==dfn[x]){
minn[++cnt]=n+1;
maxn[cnt]=0;
while(x!=find){
find=Stack[top--];
flag[find]=false;
opt[find]=cnt;
if(find<=n){
minn[cnt]=min(minn[cnt],find);
maxn[cnt]=max(maxn[cnt],find);
}
}
}
return;
}
struct Segment_Tree{
int lson(int k){
return k<<1;
}
int rson(int k){
return (k<<1)|1;
}
void build(int k,int l,int r){
id[k]=++num;
if(l==r){
add(id[k],l);
return;
}
int mid=(l+r)/2;
build(lson(k),l,mid);
build(rson(k),mid+1,r);
add(id[k],id[lson(k)]);
add(id[k],id[rson(k)]);
return;
}
void modify(int k,int l,int r,int lx,int rx,int leaf_id){
if(l>=lx&&r<=rx){
add(leaf_id,id[k]);
return;
}
int mid=(l+r)/2;
if(lx<=mid){
modify(lson(k),l,mid,lx,rx,leaf_id);
}
if(rx>mid){
modify(rson(k),mid+1,r,lx,rx,leaf_id);
}
return;
}
}xds;
void init(){
cin>>n;
num=n;
xds.build(1,1,n);
for(int i=1;i<=n;i++){
cin>>p[i]>>r[i];
}
for(int i=1;i<=n;i++){
int L=lower_bound(p+1,p+1+n,p[i]-r[i])-p;
int R=upper_bound(p+1,p+1+n,p[i]+r[i])-p-1;
// cout<<L<<" "<<R<<endl;
xds.modify(1,1,n,L,R,i);
}
return;
}
void twice_build(){
for(int i=1;i<=tot;i++){
if(opt[fa[i]]!=opt[to[i]]){
edge[opt[fa[i]]].push_back(opt[to[i]]);
indegree[opt[to[i]]]++;
}
}
return;
}
void top_sort(){
int head=1,tail=1;
for(int i=1;i<=cnt;i++){
if(!indegree[i]){
q[tail++]=i;
}
}
int now,Size,u;
while(head<tail){
now=q[head++];
Size=edge[now].size();
for(int i=0;i<Size;i++){
u=edge[now][i];
indegree[u]--;
if(!indegree[u]){
q[tail++]=u;
}
}
}
for(int i=tail-1;i;i--){
now=q[i];
Size=edge[now].size();
for(int j=0;j<Size;j++){
u=edge[now][j];
minn[now]=min(minn[now],minn[u]);
maxn[now]=max(maxn[now],maxn[u]);
}
}
return;
}
void solve(){
twice_build();
// debug();
top_sort();
int ans=0;
for(int i=1;i<=n;i++){
ans=(ans+i*(maxn[opt[i]]-minn[opt[i]]+1)%mod)%mod;
}
cout<<ans<<endl;
}
int main(){
init();
for(int i=1;i<=num;i++){
if(!dfn[i]){
tarjan(i);
}
}
// for(int i=1;i<=n;i++){
// cout<<dfn[i]<<" "<<low[i]<<endl;
// }
solve();
return 0;
}
}
signed main(){
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
WYL::main();
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号