模板 KMP算法

概念

KMP算法是来自最朴素的暴力匹配子串算法的优化。 它的优化在于暴力做法匹配失败时字符串只递进一位继续重新匹配这一步骤。
对于一些匹配失败后的情况是可以直接跳过的，但是如果每次都去做判断时间性能开销大。
所以KMP实现需要预先维护一个Next[i]数组
假设next[i]=j 有字符串s[1,j]=s[i-j+1,i]

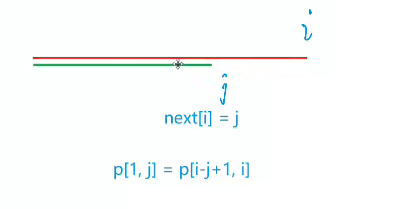
也可以说成最大的前缀和后缀匹配长度。
例子

//假设有字符串"ABABABA"
//这里的前缀的定义为除最后一个字母的子串
//后缀的定义为除第一个字母的字串  所以单个字符没有前缀和后缀
//下标为1时串为A next[1]=0
//2时串为AB 前缀为A 后缀为B 不匹配 next[2]=0
//3时前缀为A,AB 后缀为BA,A  有匹配长度为1 next[3]=1
//以此类推...

匹配实例：

这里j=6时匹配失败,就跳到next[6]=4的位置

因为P的3456保证了与S的3456相同,而定义出发next[6]=4意思就是此时的最大前缀和后缀匹配长度为4.

有表达式 S(3,4,5,6)=P(3,4,5,6)=P(1,2,3,4) 即此时P的前4个字符保证是匹配的,只需要从下一个字符开始匹配即可。这就是KMP优化的思想！！！！！！！！！！！

例题

https://www.acwing.com/problem/content/833/

#include <iostream>
#include<algorithm>
#include<cstdio>
#include<vector>
#include<queue>
#include<stack>
#include<cstring>
using namespace std;
const int N=1e5+5;
const int M=1e6+5;
int n,m;
char p[N],s[M];
int ne[N];//next数组
int main(){
    cin>>n>>p+1>>m>>s+1;//下标从1开始

    //初始化next数组
    for(int i=2,j=0;i<=n;i++){
        while(j && p[i]!=p[j+1]) j=ne[j];
        if(p[i]==p[j+1]) j++;
        ne[i]=j;
    }

    //小的串从0开始,大的串从1开始 错1位
    //错一位原因在于p[j+1]需要去判断是否匹配再去做 代码好写
    for(int i=1,j=0;i<=m;i++){
        while(j && s[i]!=p[j+1]){
            j=ne[j];//此时不匹配 按照KMP算法j跳到next[j]位置
        }
        if (s[i] == p[j + 1]) j ++ ;//如果正常匹配就继续循环
        if(j==n){
            //已经匹配完毕
            printf("%d ", i - n);
            j = ne[j];//匹配完毕后面可能还有 继续做同样的操作
        }
    }
  return 0;
}
//  freopen("testdata.in", "r", stdin);