树状数组

先来讲一下原理是什么 先上一张树状数组的状态图

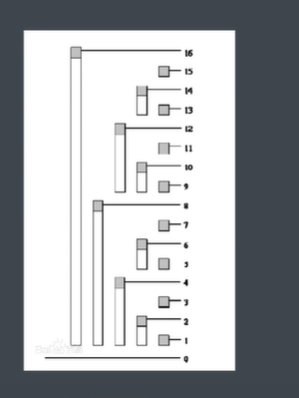
假设题目原数组为A[1]至A[16] 树状数组我们用C[n]表示

根据图 可以得知c[14]=a[13]+a[14] c[9]=a[9] c[12]=a[9]+...a[12]这样的例子

那么储存的个数取决于什么呢 我们来看看他们的二进制表达

14=1110 9=1001 12=1100

树状数组存储的元数个数等于2^k(k为其二进制末尾0的个数) 因此C[14]有2 ^ 1个数元素,C[9]有2 ^ 0个数元素,以此类推.

求和操作的实现

如果我想要获得前15个元素之和要怎么做呢？

通过图可以发现前15个元素和=C[15]+C[14]+C[12]+C[8]

同样的我们来看看他们的二进制表达 15=1111 14=1110 12=1100 8=1000

有没有发现每次都是在最末尾的1位置减1？(一直抹到最前面的1)

我们可以再来一个例子 前7个元素之和=C[7]+C[6]+C[4]

7=111 6=110 4=100

二进制就是这么神奇(前人的智慧结晶)

修改操作的实现

但是为了解决动态前缀和问题 我们还要解决修改数值的问题 再上一次图

假设我们修改了A[7]的值 根据图中我们需要修改C[7]C[8]C[16]的值

同样我们来看二进制 7=111 8=1000 16=10000

上面那个是在最末尾的1上-1,不难猜出修改其实就是在最末尾的1的位置上加1(不能大于元素的个数)

7=111+001=8 8=1000+1000=16

又比如要修改第3个元素就要修改C[3]C[4]C[8]C[16]

3=11+01=100=4 4=100+100=1000=8 8=1000+1000=16

结论

所以树状数组求和操作的实现为每次都是在最末尾的1位置减1 修改的操作为每次都是在最末尾的1位置加1

所以实现代码最重要的部分就是在于我们如何获得最末尾的1 代码如下

int lowbit(int x){
    return x&(-x);
}

具体原理用语言不是很好描述..试几个数据看看

9=1001 -9=0110+1=0111 1001&0111=0001 即最末尾的1
8=1000 -8=0111+1=1000 1000&1000=1000

知道了上面的原理后 代码实现非常简单

例题洛谷P3374

#include<iostream>
#define lb() i&-i
using namespace std;
int n,m,tree[500001];
void add(int x,int k)
{
    for(int i=x;i<=n;i+=lb())//修改的操作为每次都是在最末尾的1位置加1 i+=lb()
      tree[i]+=k;
}
int find(int x)
{
    int sum=0;
    for(int i=x;i;i-=lb())//求和操作的实现为每次都是在最末尾的1位置减1 i-=lb()
      sum+=tree[i];
    return sum;
}
int main()
{
    cin>>n>>m;

    for(int i=1;i<=n;i++)
    {
        int a;
        cin>>a;
        add(i,a);
    }
    for(int i=1;i<=m;i++)
    {
        int t,x,y;
        cin>>t>>x>>y;
        if(t==1)
          add(x,y);
        else
          cout<<find(y)-find(x-1)<<endl;
    }
    return 0;
}

参考视频