《算法图解》第六章笔记_广度优先搜索
软件环境:Python 3.7.0b4
一、算法描述
假设你经营着一家芒果农场,需要寻找芒果销售商,以便将芒果卖给他。为此,我们可以通过广度优先搜索算法,在朋友中查找出符合条件的芒果销售商。
广度优先搜索是一种用于图的查找算法,可帮助我们回答两类问题:
- 第一类问题:从节点A出发,有前往节点B的路径吗?(在你的人际关系网中,有芒果销售商吗?)
- 第二类问题:从节点A出发,前往节点B的哪条路径最短?(哪个芒果销售商与你的关系最近?)
二、实现图
将下列关系图用散列表实现
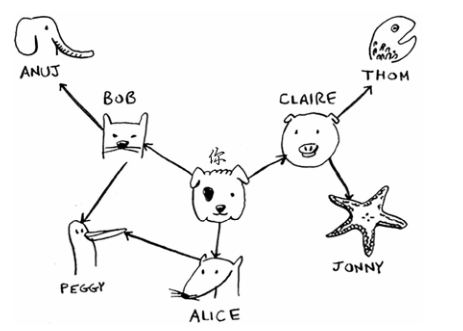
graph = {} graph["you"] = ["alice", "bob", "claire"] graph["bob"] = ["anuj", "peggy"] graph["alice"] = ["peggy"] graph["claire"] = ["thom", "jonny"] graph["anuj"] = [] graph["peggy"] = [] graph["thom"] = [] graph["jonny"] = []
注:Anuj、Peggy、Thom和Jonny都没有邻居,这是因为虽然有指向他们的箭头,但没有从他们出发指向其他人的箭头。这被称之为有向图(directed graph),其中的关系是单向的。而无向图(undirected graph)没有箭头,直接相连的节点互为邻居。
三、实现算法
概述广度优先搜索算法的工作原理:
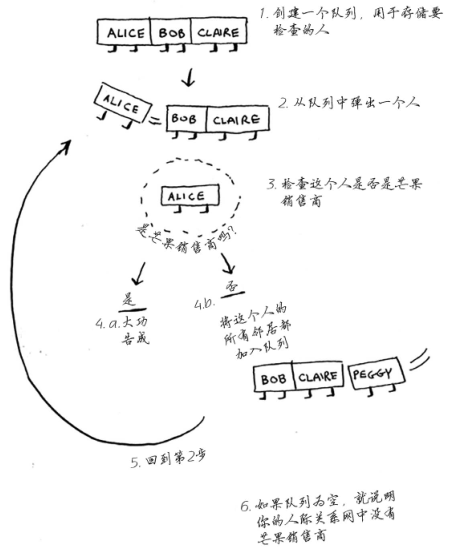
完整实现代码如下:
from collections import deque def person_is_seller(name): return name[-1] == 'm' graph = {} graph["you"] = ["alice", "bob", "claire"] graph["bob"] = ["anuj", "peggy"] graph["alice"] = ["peggy"] graph["claire"] = ["thom", "jonny"] graph["anuj"] = [] graph["peggy"] = [] graph["thom"] = [] graph["jonny"] = [] def search(name): search_queue = deque() # 创建一个队列 search_queue += graph[name] # 将你的邻居都加入到这个搜索队列中 searched = [] # 该数组用于记录检查过的人 while search_queue: # 只要队列不为空 person = search_queue.popleft() # 就取出其中的第一个人 if not person in searched: # 仅当这个人没检查过时才检查 if person_is_seller(person): # 检查这个人是否是芒果销售商 print (person + " is a mango seller!") # 是芒果销售商 return True else: search_queue += graph[person] # 不是芒果销售商。将这个人的朋友都加入搜索队列 searched.append(person) # 将这个人标记为检查过 return False # 队列中没人是芒果销售商 search("you")

四、小结
- 队列是先进先出的。
- 栈是后进先出的。
- 你需要按加入顺序检查搜索列表中的人,否则找到的就不是最短路径,因此搜索列表必须是队列。
- 对于检查过的人,务必不要再去检查,否则可能导致无限循环。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号