CodeForces 2500及以上 杂题记录

CF1556F Sports Betting
题目传送门

咕咕咕

 

CF1550E Stringforces

题目传送门

咕咕咕

  

CF1548C The Three Little Pigs

题目传送门

咕咕咕

  

CF1539E Game with Cards

题目传送门

咕咕咕

 

CF1527E Partition Game

题目传送门

记 $dp_{i,j}$ 表示前 $i$ 个元素分成 $j$ 段的最小代价。

转移是 $dp_{i, j} = \min\limits_{k = 0}^{i - 1} dp_{k, j - 1} + w_{k + 1, i}$。

然后考虑 $w_{l, r}$ 怎么算。

不难发现当 $a_r$ 在 $l \sim r - 1$ 中出现过的时候，$w_{l, r} = w_{l, r - 1} + r - last_{a_r}$，否则 $w_{l, r} = w_{l, r - 1}$。

换句话说，$w_{l, r} = \begin{cases} w_{l, r - 1} & last_{a_r} < l \\ w_{l, r - 1} + r - last_{a_r} & last_{a_r} \ge l \end{cases}$。

然后考虑 $r$ 从 $1 \sim n$ 变化时 $w_{l, r}$ 的变化情况。

记 $W_l$ 表示当前 $r$ 下的 $w_{l, r}$，不难发现 $r - 1$ 变化为 $r$ 的时候 $W$ 仅有 $1 \sim last_{a_r}$ 的一段前缀会加 $r - last_{a_r}$。

所以区间加，区间求 min，线段树维护即可。

时间复杂度 $O(kn \log{n})$

 

CF1521D Nastia Plays with a Tree

题目传送门

题目可以转化为将树分成若干条链，然后拼起来。

考虑如何使链数最小。

考虑将一个点分成两类：

1. 连接了它的两个儿子，断开与父亲的连边；

2. 至多连接它的一个儿子，连向父亲。

一个贪心策略是把节点尽可能的处理成 1 类点，处理不了再处理成 2 类点。

可以证明对于一个节点，如果既可以作为 1 类点，又可以作为 2 类点，则作为 1 类点一定不劣于 2 类点。

所以直接贪心即可。

 

CF1823E Removing Graph

题目传送门

考虑推一推 SG 函数。

由于原图是若干个简单环，所以去掉一个联通子图后会将一个环断成一条链。

不妨将环和链分开考虑，记长为 $i$ 链的 SG 函数为 $f_i$，则有 $f_i = \text{mex}_{j \in [l, r], k \in [0, i - j]}{(f_k \oplus f_{i - j - k})}$。

由于一个环删掉一个联通子图会变成一条链，所以记大小为 $i$ 的环的 SG 函数为 $g_i$，则有 $g_i = \text{mex}_{j \in [l, r]}\ f_{i - j}$。

但发现直接推时间复杂度爆炸，所以考虑打表找规律。

打表发现 $g_i = \begin{cases}\left\lfloor\dfrac{i}{l}\right\rfloor&l + r > i\\0&l + r \le i\end{cases}$。

直接计算即可。

 

CF1567F One-Four Overload

题目传送门

首先考虑无解。发现当一个标记点周围有奇数个未标记点，就是无解。

然后考虑构造有解情况。

发现一个未标记点的限制只和与它坐标和的奇偶性相等的点有关（坐标和形如 $x + y$），所以可以将原图拆成两张图考虑。

然后分类讨论。

当一个点周围有 $0$ 个未标记点时，这个点值为 $0$，周围的点没有任何限制。

当一个点周围有 $2$ 个未标记点时，这个点值为 $5$，周围的两个未标记点连一条限制边。

当一个点周围有 $4$ 个未标记点时，这个点值为 $10$，周围的点只要相邻点连限制边即可。

但这样连会出问题。

原因是周围有 $4$ 个未标记点时限制过强了，所以可能构造不出可行解。

所以考虑 $4$ 个点的情况减弱一点限制。

发现只要两对 $1, 4$ 即可，所以将限制边个数减为 $2$ 条，此时有以下两种选择：

 

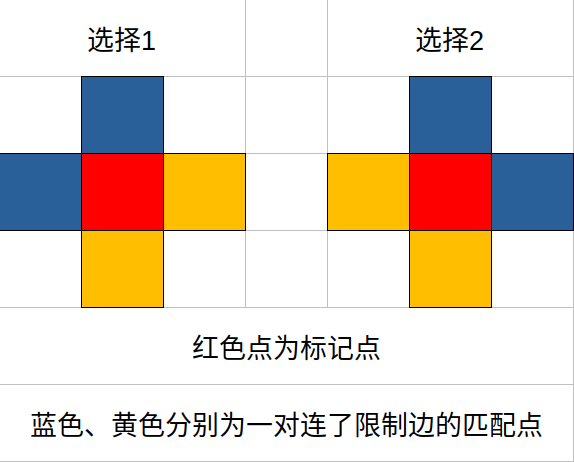
再优化一下，按照两种选择里已连的限制边个数多的那种连边即可。

 

 

CF1783F Double Sort II

题目传送门

首先不难发现题目可以转化为每次选定一个 $i$，并从 $P_a, P_b$ 中包含 $i$ 的置换环里删去 $i$。

不难发现每个环对于最优策略会删 $siz - 1$ 个点（$siz$ 为环的大小），不妨将一个点 $i$ 在 $P_a, P_b$ 里对应的环连边，所以题意转化为有两组置换环 $A, B$，每组中有若干个置换环，两组中的有些置换环之间有连边，形成二分图，求最大匹配。

匈牙利算法或网络流均可实现，匈牙利算法时间复杂度 $O(n^2)$，网络流（Dinic 算法）时间复杂度 $O(n \sqrt{n})$。

 

CF1437G Death DBMS

题目传送门

发现查询字符串总长度不超过 $3 \times 10 ^ 5$，所以考虑建 AC 自动机。

由于查询的是子串权值 max，每次查询相当于在 fail 树上的一条到根的链，但暴力查复杂度是错的，所以考虑优化。

因为 fail 的形态是一棵树，而操作形式是单点修改，链上查询，树剖维护即可。