期望

期望本身有个公式，但可惜这个公式用的并不多。

使用最多的是期望的线性性的公式，因为这个公式可以将我们要求的答案拆成若干份，这样我们就可以正常的计算了，只要是各部分不会互相影响的都可以考虑期望线性性。

期望可以理解为到某步预估的某值，所以不必考虑各种概率产生的多种情况分支。

期望可以往dp上考虑,常见dp[i][j]代表考虑到第i个，选了j个（每个选择有概率）（可能还要加一维最后一个值选或不选（例）），如果一个东西选的概率不好考虑（比如概率在选完会变化），可以考虑选不到的概率。（例，当然这题还有好多能借鉴的东西。）
从n个东西里选，每次n个物品等概率，若要求全部取完的期望次数，则可：


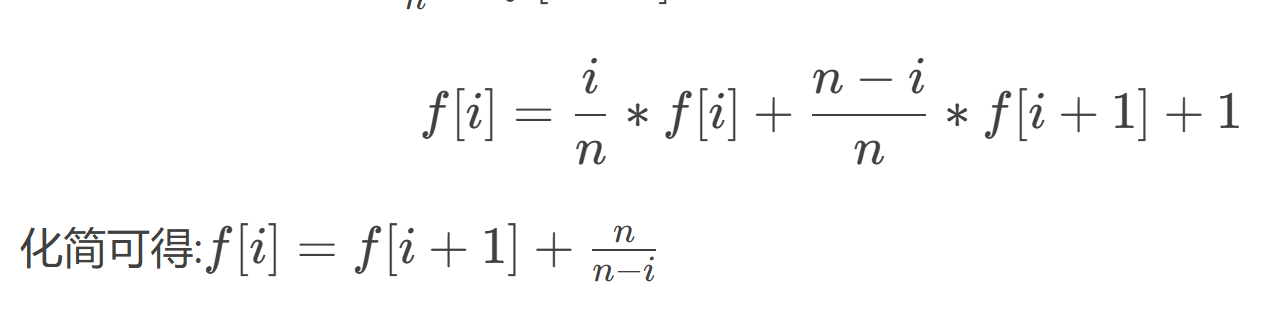
若要每次需要价钱，则可在设一个别的，用f联合着推。（例）

如果出现像每一步既有可能向前走也可能往回走或回到起点这种正着推不好推的，可以反着推，\(f[i]\)代表从i到n的期望。例，当然这个题并不要真的动态规划，而是求出递推式后再推出\(f[0]\)

可以先从最基础的情况推起，再扩展到别的。例