[信友队图灵杯中级组-D]基础循环结构练习题

2023-5-13

题目

题目传送门

难度&重要性(1~10):6.5

题目来源

信友队图灵杯

题目算法

构造

解题思路

我们可以知道，在一开始我们得到的 \(a\) 数组是 \(1,2,3, \dots n\)。
所以我们可以看做是：

题目让我们构造出一个 \(b\) 数组。
因为数据是 \(1\le n\le 10^3,1\le b_i \le 10^5\)，而他要求我们最多要在 \(2001\) 次修改以内得到。
所以我们就要考虑最多每两次操作得到一个 \(b_i\)，且不对其他数有所影响。
我们要用 \(\mod(\ge 1e5+3)\) 去代替减法操作。
考虑每次从对最大的修改。

然后我们需要将 \(b_i\) 分解一下，分解成查分形式。
记 \(c_i=b_i-b_{i-1}\)
故 \(b_i=\sum\limits_{j=1}^ic_j\)

最后，我们怎么确定每一次的最大值呢？
答案是我们只需要从后向前修改就行了。
因为，每次对 \(a_i\) \(mod\) 后就归零了，即使最小值，而因为每次做加时是整体加的。
就像下图：

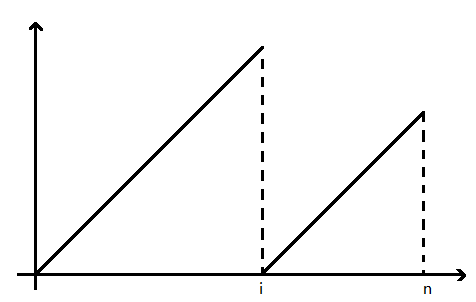
从后往前修改：

• 先将 \(a_n \mod n\)，\(n \rightarrow 0\)。
• 在整体加上 \(c_n\)。

以此类推。

完成状态

已完成